Viết bài văn nghị luận phân tích chủ đề vag đặc sắc nghệ thuật của 1 đoạn trích hay tác phẩm THƠ TƯỢNG TRƯNG.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(u_{n+1}=u_n+\dfrac{1}{n\left(n+1\right)}\Rightarrow u_{n+1}=u_n+\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(\Rightarrow u_{n+1}+\dfrac{1}{n+1}=u_n+\dfrac{1}{n}\)
Đặt \(u_n+\dfrac{1}{n}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1+\dfrac{1}{1}=2\\v_{n+1}=v_n\end{matrix}\right.\)
Từ \(v_{n+1}=v_n\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=2\)
\(\Rightarrow v_n=2\Rightarrow u_n+\dfrac{1}{n}=2\)
\(\Rightarrow u_n=2-\dfrac{1}{n}=\dfrac{2n-1}{n}\)
\(\Rightarrow u_{2024}=\dfrac{2.2024-1}{2024}=\dfrac{4047}{2024}\)

a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SAD\right)\)
b.
\(V=\dfrac{1}{3}SA.AB.AD=2a^3\)



- Cả hai cuộc cải cách đều thúc đẩy sự hoàn thiện từng bước của bộ máy nhà nước.
- Thúc đẩy sự phát triển và từng bước giữ vị thế độc tôn của Nho giáo.
- Giáo dục, khoa cử được chú trọng và có nhiều bước tiến mới.
- Cả hai cuộc cải cách đều thể hiện tinh thần dân tộc, ý thức tự lực, tự cường sâu sắc.
- Để lại nhiều bài học kinh nghiệm cho các cuộc cải cách sau đó.

Câu 3:
\(P\left(AB\right)=P\left(A\right)\cdot P\left(B\right)=0,9\cdot0,7=0,63\)
\(P\left(\overline{A}\right)=1-0,9=0,1;P\left(\overline{B}\right)=1-0,7=0,3\)
\(P\left(\overline{A}B\right)=0,1\cdot0,7=0,07\)
\(P\left(\overline{A}\overline{B}\right)=0,1\cdot0,3=0,03\)
Câu 1:
\(y=x^4-x+1\)
=>\(y'=4x^3-1\)
\(y'\left(2\right)=4\cdot2^3-1=4\cdot8-1=31\)
Phương trình tiếp tuyến tại M là:
y-y(2)=y'(2)(x-2)
=>y-15=31(x-2)
=>y-15=31x-62
=>y=31x-62+15=31x-47
\(P\left(AB\right)=P\left(A\right).P\left(B\right)=0,9.0,7=0,63\)
\(P\left(\overline{A}B\right)=P\left(B\right)-P\left(AB\right)=0,7-0,63=0,07\)
\(P\left(\overline{AB}\right)=1-P\left(AB\right)=0,37\)


Gọi M là trung điểm EG \(\Rightarrow AM\perp EG\) (tam giác cân)
\(\Rightarrow AM\perp\left(EFGH\right)\Rightarrow AM=d\left(A;\left(EFGH\right)\right)\)
\(EG=30-2x\Rightarrow EM=\dfrac{1}{2}EG=15-x\)
\(\Rightarrow AM=\sqrt{AE^2-EM^2}=\sqrt{x^2-\left(15-x\right)^2}=\sqrt{30x-225}\)
Do AEG là tam giác, theo BĐT tam giác: \(\left\{{}\begin{matrix}AE+AG>EG\\\left|AG-AE\right|< EG\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+x>30-2x\\0< 30-2x\end{matrix}\right.\) \(\Rightarrow\dfrac{15}{2}< x< 15\)
\(V=AD.S_{\Delta AEG}=30.\dfrac{1}{2}AM.EG=15.\left(30-2x\right)\sqrt{30x-225}\)
\(V^2=15^3.4\left(15-x\right)^2\left(2x-15\right)=15^3.4.\left(15-x\right)\left(15-x\right)\left(2x-15\right)\)
\(\le15^3.4.\left(\dfrac{15-x+15-x+2x-15}{3}\right)^3=...\)
Dấu "=" xảy ra khi \(15-x=2x-15\Rightarrow x=10\)
\(\Rightarrow d\left(A;\left(EFGH\right)\right)=AM=\sqrt{30.10-225}=5\sqrt{3}\)
 ai giúp mik với tại mik đag cần gấp
ai giúp mik với tại mik đag cần gấp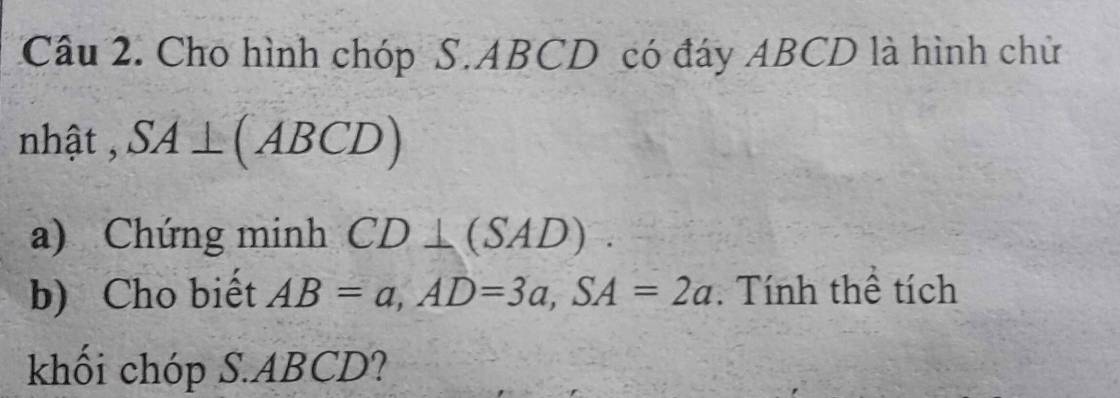 thanks nhiều
thanks nhiều

