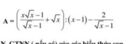
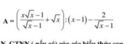
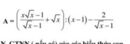
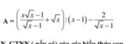
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\sqrt{4x-20}-3\sqrt{\frac{x-5}{9}}=\sqrt{1-x}\)
\(2\sqrt{x-5}-3\frac{\sqrt{x-5}}{3}=\sqrt{1-x}\)
\(2\sqrt{x-5}-\sqrt{x-5}=\sqrt{1-x}\)
\(\sqrt{x-5}=\sqrt{1-x}\)
\(ĐKXĐ:x\ge5;x\le1\)
vậy pt vô nghiệm
\(b,ĐKXĐ:x\ge2\)
\(b,\sqrt{50x-25}+\sqrt{8x-4}-3\sqrt{x}=\sqrt{72x}\)
\(5\sqrt{2x-1}+2\sqrt{2x-1}-3\sqrt{x}=6\sqrt{2x}\)
\(7\sqrt{2x+1}=6\sqrt{2x}+3\sqrt{x}\)
\(49\left(2x+1\right)=72x+9x+36\sqrt{2}x\)
\(98x+49=81x+36\sqrt{2}x\)
\(17x+49=36\sqrt{2}x\)
\(x\left(17+36\sqrt{2}\right)=-49\)
\(x=\frac{-49}{17+36\sqrt{2}}\left(KTM\right)\)
vậy pt vô nghiệm
\(c,ĐKXĐ:x\ge3\)
\(c,\sqrt{x^2-9}-\sqrt{4x-12}=0\)
\(\sqrt{x-3}\sqrt{x+3}-2\sqrt{x-3}=0\)
\(\sqrt{x-3}\left(\sqrt{x+3}-2\right)=0\)
\(\orbr{\begin{cases}\sqrt{x-3}=0\\\sqrt{x+3}-2=0\end{cases}}\orbr{\begin{cases}x=3\left(TM\right)\\x=1\left(KTM\right)\end{cases}}\)
\(d,ĐKXĐ:x\ge-1\)
\(\sqrt{9x+9}-2\sqrt{\frac{x+1}{4}}=4\)
\(3\sqrt{x+1}-2\frac{\sqrt{x+1}}{2}=4\)
\(2\sqrt{x+1}=4\)
\(x+1=4\)
\(x=3\left(TM\right)\)

\(K=x+2\sqrt{x-1}=x-1+2\sqrt{x-1}+1=\left(\sqrt{x-1}+1\right)^2\ge\left(0+1\right)^2=1\)
Dấu ''='' xảy ra khi \(\sqrt{x-1}=0\Leftrightarrow x=1\)
Vậy GTNN K bằng 1 tại x = 1

Áp dụng BĐT Cauchy Schwarz dạng Engel
\(A\ge\frac{\left(1+1+1\right)^2}{a^2+ab+b^2+bc+ca+c^2}\)
Theo BĐT : \(a^2+b^2+c^2\ge ab+ac+bc\)
\(2a^2+2b^2+2c^2\ge2ab+2ac+2bc\)
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)* đúng *
\(=\frac{\left(1+1+1\right)^2}{2\left(ab+ac+bc\right)}=\frac{9}{2.3}=\frac{3}{2}\)
Dấu ''='' xảy ra khi a = b = c = 1

ta có \(xy\le\frac{x^2+y^2}{2}\Rightarrow\frac{x^2}{x^2+xy+y^2}\ge\frac{2}{3}.\frac{x^2}{x^2+y^2}\)
Vậy \(A\ge\frac{2}{3}\left(\frac{x^2}{x^2+y^2}+\frac{y^2}{y^2+z^2}+\frac{z^2}{z^2+x^2}\right)=\frac{2}{3}\left(\frac{x^2+y^2+z^2}{x^2+y^2}-1+\frac{x^2+y^2+z^2}{y^2+z^2}-1+\frac{x^2+y^2+z^2}{x^2+z^2}-1\right)\)
hay \(A\ge\frac{2\left(x^2+y^2+z^2\right)}{3}\left(\frac{1}{x^2+y^2}+\frac{1}{y^2+z^2}+\frac{1}{z^2+x^2}\right)-2\)
\(\Rightarrow A\ge\frac{2}{3}\left(x^2+y^2+z^2\right).\frac{9}{2\left(x^2+y^2+z^2\right)}-2=3-2=1\)
Vậy ta có đpcm

ta có :
\(B=\left(\frac{1}{\sqrt{x}+1}-\frac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\frac{x-\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\left(\frac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\frac{1}{\sqrt{x}+1}=\frac{\sqrt{x}-1}{\sqrt{x}}\)

ta có
\(S\ge\frac{1}{\frac{1+1998}{2}}+\frac{1}{\frac{2+1997}{2}}+..+\frac{1}{\frac{k+1998-k+1}{2}}+..+\frac{1}{\frac{1999}{2}}\)
hay \(S\ge\frac{2}{1999}+\frac{2}{1999}+..+\frac{2}{1999}=2.\frac{1998}{1999}\)
do dấu = không xảy ra nên \(S>2.\frac{1998}{1999}\)

\(a,\sqrt{\left(3-\sqrt{5}\right)^2}+2\sqrt{5}=3-\sqrt{5}+2\sqrt{5}\)
\(=3+\sqrt{5}\)
\(b,\sqrt{9a^2}-\sqrt{\left(a-3\right)^2}\)
\(\sqrt{\left(3a\right)^2}-\left|a-3\right|\)
\(\left|3a\right|-a+3\)
\(2a+3\)
bài 5
\(a,\sqrt{\left(5-x\right)^2}=3\)
\(\left|5-x\right|=3\)
\(\orbr{\begin{cases}5-x=3\\5-x=-3\end{cases}\orbr{\begin{cases}x=2\left(TM\right)\\x=8\left(TM\right)\end{cases}}}\)
\(b,\sqrt{3x}-\sqrt{48x}+\sqrt{75x}=8\)
\(\sqrt{3x}\left(1-4+5\right)=8\)
\(\sqrt{3x}.0=8\left(KTM\right)\)
vậy pt vô nghiệm
giải hệ phương trình sau:
\(\hept{\begin{cases}x+y-\sqrt{xy}=3\\\sqrt{x+1}+\sqrt{y+1}=4\end{cases}}\)

\(\sqrt{x+1}+\sqrt{y+1}=4\Leftrightarrow x+y+2+2\sqrt{xy+x+y+1}=16\)
mà \(x+y=3+\sqrt{xy}\)nên ta có
\(5+\sqrt{xy}+2\sqrt{xy+\sqrt{xy}+4}=16\Leftrightarrow2\sqrt{xy+\sqrt{xy}+4}=11-\sqrt{xy}\)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{xy}\le11\\4\left(xy+\sqrt{xy}+4\right)=121-22\sqrt{xy}+xy\end{cases}\Leftrightarrow\hept{\begin{cases}\sqrt{xy}\le11\\3xy+26\sqrt{xy}-105=0\end{cases}}}\)
\(\Leftrightarrow\sqrt{xy}=3\Leftrightarrow\hept{\begin{cases}x+y=6\\xy=9\end{cases}}\Leftrightarrow x=y=3\)
\(A=\left(\frac{x\sqrt{x}-1}{\sqrt{x}-1}+\sqrt{x}\right):\left(x-1\right)-\frac{2}{\sqrt{x}-1}\)ĐK : \(x\ge0;x\ne1\)
\(=\left(\frac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}-1}+\sqrt{x}\right):\left(x-1\right)-\frac{2}{\sqrt{x}-1}\)
\(=\left(x+2\sqrt{x}+1\right):\left(x-1\right)-\frac{2}{\sqrt{x}-1}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}-1}-\frac{2}{\sqrt{x}-1}=1\)