Chohàmsố ym1x2mdvới m1.
a)Tìm m để dcóhệsốgócbằng 2.
b) Tìm m để d cắt trục hoành tại điểm có hoành độ bằng 3. c)Tìm m để dcắttrụctungtạiđiểmcótungđộbằng 2. d)Tìmm đểdsongsongvớiđườngthẳngd1:y3x4.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Giả sử theo kế hoạch tổ sản xuất trong $n$ ngày.
Số sản phẩm theo kế hoạch: $50n$ (sản phẩm)
Số sản phẩm thực tế: $57(n-1)$ (sản phẩm)
Theo bài ra ta có:
$57(n-1)=50n+13$
$\Leftrightarrow 7n=70$
$\Leftrightarrow n=10$
Theo kế hoạch tổ phải sản xuất số sản phẩm là:
$50n=50.10=500$ (sản phẩm)
Gọi số sp tổ phải sản xuất theo kế hoạch là: x(sản phẩm) ĐK:x>13
\(\Rightarrow\)Thời gian dự định làm là: \(\dfrac{x}{50}\)(ngày)
Thời gian thực tế là: \(\dfrac{x+13}{57}\)(ngày)
Theo bài ra ta có pt:
\(\dfrac{x}{50}\)-\(\dfrac{x+13}{57}\)=1
\(\Leftrightarrow\)2850(\(\dfrac{x}{50}\)-\(\dfrac{x+13}{57}\))=2850
\(\Leftrightarrow\)\(57x-50x-650=2850\)
\(\Leftrightarrow\)\(7x=3500\)
\(\Leftrightarrow\)\(x=500\)
Vậy ....

- \(\dfrac{2}{5}\)\(x^2\)y.2\(xy^3\).\(\dfrac{1}{4}\)yz
= (-\(\dfrac{2}{5}\).2.\(\dfrac{1}{4}\)).(\(x^2\).\(x\)).(y.y3.y).z
= - \(\dfrac{1}{5}\)\(x^3\).y5.z
\(-\dfrac{2}{5}x^2y\cdot2xy^3\cdot\dfrac{1}{4}yz\)
\(=\left(-\dfrac{2}{5}\cdot2\cdot\dfrac{1}{4}\right)\cdot\left(x^2\cdot x\right)\cdot\left(y\cdot y^3\cdot y\right)\cdot z\)
\(=-\dfrac{1}{5}x^3y^5z\)

Lời giải:
$\frac{a+b}{c}=\frac{b+c}{a}=\frac{c+a}{b}$
$\Rightarrow \frac{a+b}{c}+1=\frac{b+c}{a}+1=\frac{c+a}{b}+1$
$\Rightarrow \frac{a+b+c}{c}=\frac{b+c+a}{a}=\frac{a+b+c}{b}$
Do $a+b+c\neq 0$ nên $c=a=b$
Khi đó:
$A=\frac{a}{b+c}+\frac{a+b}{c}+\frac{b}{c+a}=\frac{a}{a+a}+\frac{a+a}{a}+\frac{a}{a+a}=\frac{1}{2}+2+\frac{1}{2}=3$

Gọi chiều rộng khu vườn là x(m)
(Điều kiện: x>0)
Chiều dài khu vườn là x+5(m)
Chiều dài sau khi giảm 5m là x+5-5=x(m)
Chiều rộng sau khi tăng thêm 3m là x+3(m)
Diện tích giảm 10m2 nên ta có:
x(x+5)-x(x+3)=10
=>2x=10
=>x=5(nhận)
Vậy: Chiều rộng ban đầu là 5m
Chiều dài ban đầu là 5+5=10m
Gọi chiều rộng khu vườn là x(m)
(Điều kiện: x>0)
Chiều dài khu vườn là x+5(m)
Chiều dài sau khi giảm 5m là x+5-5=x(m)
Chiều rộng sau khi tăng thêm 3m là x+3(m)
Diện tích giảm 10m2 nên ta có:
x(x+5)-x(x+3)=10
=>2x=10
=>x=5(nhận)
Vậy: Chiều rộng ban đầu là 5m
Chiều dài ban đầu là 5+5=10m
Đáp số: 10 m
xin tkkkkkkkk!!!!

Gọi số ghế của mỗi dãy ban đầu là x(ghế)
(Điều kiện: \(x\in Z^+\))
Số dãy ghế ban đầu là \(\dfrac{120}{x}\left(dãy\right)\)
Số ghế ở mỗi dãy lúc sau là x+5(ghế)
Số dãy ghế lúc sau là \(\dfrac{120+72}{x+5}=\dfrac{192}{x+5}\left(dãy\right)\)
Trường phải kê thêm 3 dãy ghế nên ta có:
\(\dfrac{192}{x+5}-\dfrac{120}{x}=3\)
=>\(\dfrac{64}{x+5}-\dfrac{40}{x}=1\)
=>\(\dfrac{64x-40x-200}{x\left(x+5\right)}=1\)
=>\(x\left(x+5\right)=24x-200\)
=>\(x^2+5x-24x+200=0\)
=>\(x^2-19x+200=0\)
=>\(x\in\varnothing\)
Vậy: Không có số liệu nào thỏa mãn yêu cầu đề bài
Giải:
Gọi số ghế lúc đầu của mỗi dãy là: \(x\) (ghế); \(x\) \(\in\) N*
Số dãy ghế ban đầu là: 120 : \(x\) = \(\dfrac{120}{x}\)
Tổng số ghế lúc sau là: 120 + 72 = 192 (ghế)
Số dãy ghế lúc sau là: \(\dfrac{192}{x+5}\)
Theo bài ra ta có: \(\dfrac{192}{x+5}-\dfrac{120}{x}\) = 3
\(\dfrac{64}{x+5}-\dfrac{40}{x}=1\)
64\(x\) - 40\(x\) - 200 = .\(x\).(\(x\) + 5)
24\(x\) - 200 = \(x^2\) + 5\(x\)
\(x^2\) + 5\(x\) - 24\(x\) + 200 = 0
\(x^2\) + (5\(x-24x\)) + 200 = 0
\(x^2\) - 19\(x\) + 200 = 0
\(x^2\) - 2.\(\dfrac{19}{2}\)\(x\) + \(\dfrac{361}{4}\) + \(\dfrac{439}{4}\) = 0
(\(x-\dfrac{19}{2}\))2 + \(\dfrac{439}{4}\) = 0
(\(x-\dfrac{19}{2}\))2 ≥ 0 \(\forall\) \(x\)
⇒ (\(x-\dfrac{19}{2}\))2 + \(\dfrac{439}{2}\) ≥ \(\dfrac{439}{2}\) > 0 ∀ \(x\)
Vậy \(x\in\) \(\varnothing\)
Kết luận không có số ghế ban đầu của mỗi dãy nào thỏa mãn đề bài.

\(x^2+x-2\)
\(=x^2+x+\dfrac{1}{4}-\dfrac{9}{4}\)
\(=\left(x+\dfrac{1}{2}\right)^2-\dfrac{9}{4}>=-\dfrac{9}{4}\forall x\)
Dấu '=' xảy ra khi \(x+\dfrac{1}{2}=0\)
=>\(x=-\dfrac{1}{2}\)

a: Sửa đề: ΔAHB~ΔBCD
Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//CD)
Do đó; ΔAHB~ΔBCD
b: ΔBCD vuông tại C
=>\(BC^2+CD^2=BD^2\)
=>\(BD=\sqrt{12^2+9^2}=15\left(cm\right)\)
ΔAHB~ΔBCD
=>\(\dfrac{AH}{BC}=\dfrac{AB}{BD}\)
=>\(\dfrac{AH}{9}=\dfrac{12}{15}=\dfrac{4}{5}\)
=>\(AH=4\cdot\dfrac{9}{5}=7,2\left(cm\right)\)
c: ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB=\sqrt{12^2-7,2^2}=9,6\left(cm\right)\)
ΔAHB vuông tại H
=>\(S_{HAB}=\dfrac{1}{2}\cdot HA\cdot HB=\dfrac{1}{2}\cdot7,2\cdot9,6=4,8\cdot7,2=34,56\left(cm^2\right)\)

`#3107.101107`
Hình chóp là tam giác đều hay tứ giác đều nhỉ? Mình làm mẫu 1 cái nhé
Diện tích của mặt đáy hình chóp tứ giác (tam giác) đều:
\(\text{S}_{\text{xq}}=a^2=10^2=100\left(\text{cm}^2\right)\)
(\(\text{S}_{\text{xq}}=\dfrac{1}{2}\cdot a\cdot h=\dfrac{1}{2}\cdot5\cdot10=25\left(\text{cm}^2\right)\))
Thể tích của hình chóp tứ giác (tam giác) đều:
\(\text{V}_{\text{hình chóp}}=\dfrac{1}{3}\cdot s\cdot h=\dfrac{1}{3}\cdot100\cdot5\approx166,7\left(\text{cm}^3\right)\)
(\(\text{V}_{\text{hình chóp}}=\dfrac{1}{3}\cdot s\cdot h=\dfrac{1}{3}\cdot25\cdot10\approx83,3\left(\text{cm}^3\right).\))

Một phân thức đại số (hay nói gọn là phân thức) là một biểu thức có dạng \(\dfrac{A}{B}\), trong đó \(A,B\) là những đa thức và \(B\ne0\)
\(A\) được gọi là tử thức (hay tử) , \(B\) được gọi là mẫu thức (hay mẫu)
\(\Rightarrow\dfrac{2+3}{x}\) là phân thức đại số.
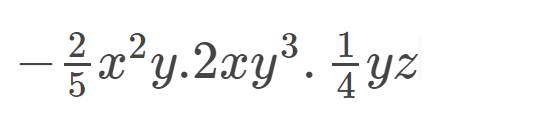
Đề hiển thị lỗi tùm lum hết trơn. Bạn xem lại nhé.