 gấpppp giúppp e vsss
gấpppp giúppp e vsss
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AO là đường trung trực của BC
b: Xét (O) có
ΔCBD nội tiếp
CD là đường kính
Do đó: ΔCBD vuông tại B
=>CB\(\perp\)BD
mà AO\(\perp\)BC
nên AO//BD

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}=\dfrac{3}{4}\)
nên \(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-37^0=53^0\)
b: Xét ΔBDC vuông tại B có BA là đường cao
nên \(BA^2=AD\cdot AC\)
=>\(AD=\dfrac{3^2}{4}=\dfrac{9}{4}=2,25\left(cm\right)\)
ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD=\sqrt{2,25^2+3^2}=3,75\left(cm\right)\)
Xét ΔBAD vuông tại A có AF là đường cao
nên \(BF\cdot BD=BA^2\left(1\right)\)
Xét ΔBAC vuông tại A có AE là đường cao
nên \(BE\cdot BC=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BF\cdot BD=BE\cdot BC\)
Xét tứ giác AEBF có \(\widehat{AEB}=\widehat{AFB}=\widehat{EBF}=90^0\)
nên AEBF là hình chữ nhật
ΔABC vuông tại A có AE là đường cao
nên \(\left\{{}\begin{matrix}AE\cdot BC=AB\cdot AC\\BE\cdot BC=BA^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AE=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\\BE=\dfrac{3^2}{5}=1,8\left(cm\right)\end{matrix}\right.\)
AEBF là hình chữ nhật
=>\(S_{AEBF}=AE\cdot BE=2,4\cdot1,8=4,32\left(cm^2\right)\)

`sqrt{6x - 2} = 4`
`ĐKXĐ: 6x - 2 >=0 <=> x >=1/3`
`Pt <=> 6x - 2 = 16`
`<=> 6x = 18`
`<=> x = 3 ` (Thỏa mãn)
Vậy ...
ĐKXĐ: \(x\ge\dfrac{1}{3}\)
\(\sqrt{6x-2}=4\)
\(\Leftrightarrow6x-2=16\)
\(\Leftrightarrow6x=18\)
\(\Leftrightarrow x=3\)

\(\Delta'=\left(m-2\right)^2-\left(m^2-2m+2\right)=-2m+2>0\Rightarrow m< 1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\\x_1x_2=m^2-2m+2\end{matrix}\right.\)
\(\left|\left(x_1+x_2\right)+x_1x_2\right|=3\)
\(\Leftrightarrow\left|2\left(m-2\right)+m^2-2m+2\right|=3\)
\(\Leftrightarrow\left|m^2-2\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2-2=3\\m^2-2=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2=5\\m^2=-1\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\sqrt{5}>1\left(loại\right)\\m=-\sqrt{5}\end{matrix}\right.\)
Vậy \(m=-\sqrt{5}\)

Gọi thời gian làm 1 mình xong việc của người thứ nhất là x giờ, của người thứ hai là y giờ (với x;y>0)
Do người thứ nhất làm 1 mình cần nhiều hơn người thứ hai là 12 giờ nên:
\(x-y=12\) (1)
Trong 1 giờ người thứ nhất làm được \(\dfrac{1}{x}\) phần công việc
Trong 1 giờ người thứ hai làm được \(\dfrac{1}{y}\) phần công việc
Do 2 người làm chung trong 8 giờ xong việc nên:
\(8\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\Rightarrow8x+8y=xy\) (2)
Từ (1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}x-y=12\\8x+8y=xy\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y+12\\8\left(y+12\right)+8y=y\left(y+12\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y+12\\y^2-4y-96=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=12\Rightarrow x=24\\y=-8< 0\left(loại\right)\end{matrix}\right.\)

Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x(giờ) và y(giờ)
(Điều kiện: x>6; y>0)
Người thứ hai hoàn thành công việc nhanh hơn người thứ nhất là 6 giờ nên x-y=6(1)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người làm được: \(\dfrac{1}{4}\)(công việc)
Do đó, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x-y=6\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+6\\\dfrac{1}{y+6}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{y+y+6}{y^2+6y}=\dfrac{1}{4}\\x=y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y^2+6y=4\left(2y+6\right)=8y+24\\x=y+6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y^2+6y-8y-24=0\\x=y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y^2-2y-24=0\\x=y+6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(y-6\right)\left(y+4\right)=0\\x=y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}y=6\left(nhận\right)\\y=-4\left(loại\right)\end{matrix}\right.\\x=y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=6\\x=6+6=12\end{matrix}\right.\left(nhận\right)\)
Vậy: thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là 12(giờ) và 6(giờ)

Vì: \(a>b\) nên nhân a,b với \(4\), ta có:
\(4a>4b\)
Biết: \(7>5\)
\(\rightarrow4a+7>7b+5\left(đpcm\right)\)


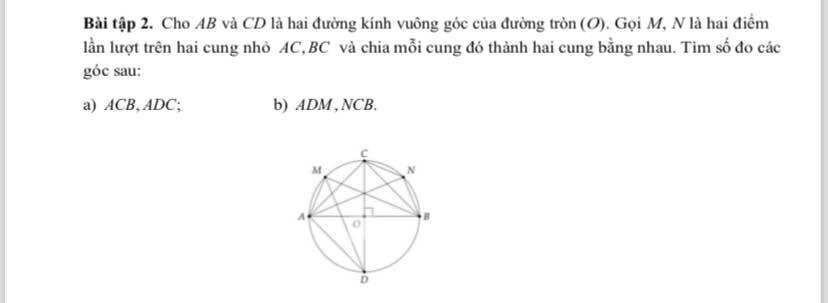
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>\(\widehat{ACB}=90^0\)
Xét (O) có \(\widehat{ADC}\) là góc nội tiếp chắn cung AC
nên \(\widehat{ADC}=\dfrac{\widehat{AOC}}{2}=\dfrac{90^0}{2}=45^0\)
b: M là điểm chia cung AC thành hai cung nhỏ bằng nhau
=>\(sđ\stackrel\frown{MA}=\dfrac{sđ\stackrel\frown{AC}}{2}=\dfrac{90^0}{2}=45^0\)
Xét (O) có \(\widehat{ADM}\) là góc nội tiếp chắn cung AM
nên \(\widehat{ADM}=\dfrac{1}{2}\cdot sđ\stackrel\frown{MA}=\dfrac{1}{2}\cdot45^0=22,5^0\)
N chia cung BC thành hai cung nhỏ bằng nhau
=>\(sđ\stackrel\frown{BN}=\dfrac{sđ\stackrel\frown{BC}}{2}=45^0\)
Xét (O) có
\(\widehat{NCB}\) là góc nội tiếp chắn cung NB
=>\(\widehat{NCB}=\dfrac{sđ\stackrel\frown{NB}}{2}=\dfrac{45^0}{2}=22,5^0\)