bài 1 : cho A = {n| \(\sqrt{n+1}\) là số tự nhiên, 2 < \(\sqrt{n+1}< 6\)}
khoanh vào khẳng định đúng
- khẳng định 1 : có 3 phần tử của A là bội của 5
- khẳng định 2 : có 3 phần tử của A là bội của 3
- khẳng định 3 : có 2 phần tử của A là bội của 3
- khẳng định 4 : có 2 phần tử của A là bội của 5
bài 2 : kí hiệu \(\left[x\right]\) là số nguyên lớn nhất không vượt quá \(x\)
cho \(x\) là số thực thỏa mãn \(\left[x\right]\div2=3\div6\), khoanh vào khẳng định đúng
- khẳng định 1 : (x - 1) × (x - 3) ≥ 0
- khẳng định 2 : (x - 1) × (x - 3) > 0
- khẳng định 3 : (x - 1) × (x - 3) ≤ 0
- khẳng định 4 : (x - 1) × (x - 3) < 0
bài 3 : cho tam giác ABC có \(\widehat{A}=62^o,\widehat{B}=52^o,AD\) là tia phân giác góc A, D thuộc BC. Tính số đo của góc ADC
bài 4 : cho 2 số \(x,y\) thỏa mãn \(x\div15=y\div6\) và \(xy=10\), khoanh vào khẳng định đúng
- khẳng định 1 : y2 < 30 < x2
- khẳng định 2 : x2 < y2 < 30
- khẳng định 3 : y2 < x2 < 30
- khẳng định 4 : x2 < 30 < y2
bài 5 : cho tam giác ABC, số đo góc A là 44o. Kẻ Bx, Cy lần lượt là tia đối của tia BA, CA. Tia phân giác của các góc xBC và BCy cắt nhau tại H. Tính số đo của góc BHC
bài 6 : cho tam giác ABC có \(\widehat{A}=60^o,\widehat{B}=40^o,D\) là điểm nằm trên cạnh BC sao cho \(\widehat{DAC}=2\times\widehat{BAD}\). Tia phân giác góc B cắt AD tại M. Tính số đo góc AMB
bài 7 : căn bậc ba số thực \(a\) là số thực \(x\) sao cho x3 = a. Kí hiệu \(x=\sqrt[3]{a}\). Gia trị của \(x\) thỏa mãn \(\sqrt[3]{27x+27}+\sqrt[3]{8x+8}=5\) là :
bài 8 : cho \(x,y\) là các số thực khác 0 thỏa mãn \(x\div2=y\div7.\) Khoanh vào đẳng thức đúng nhất
- đẳng thức 1 : \(\left(x-y\right)\div\left(x+y\right)=5\div\left(-9\right)\)
- đẳng thức 2 : \(\left(x-y\right)\div\left(x+y\right)=5\div9\)
- đẳng thức 3 : \(\left(x-y\right)\div\left(x+y\right)=\left(-9\right)\div5\)
- đẳng thức 4 : \(\left(x-y\right)\div\left(x+y\right)=9\div5\)



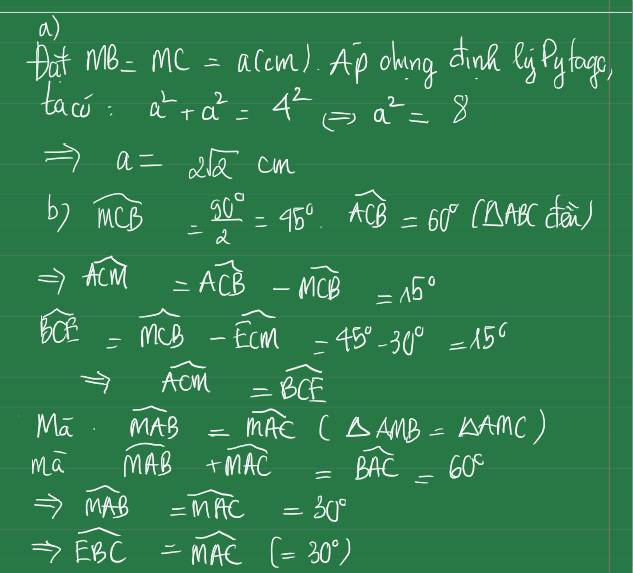
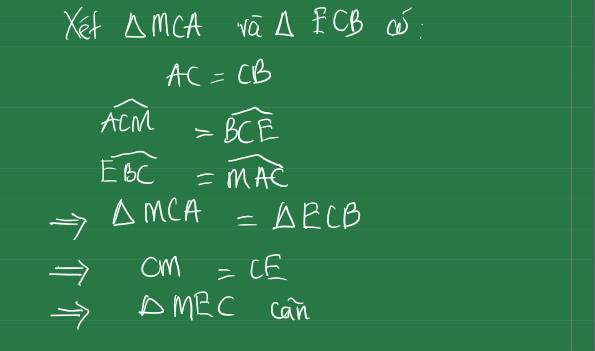
Đặt a/3=b/5=k
=>a=3.k
=>a2=9.k2
=>b=5.k
=>b2=25.k2
Ta có: C= 5a2+3b2/10a2-3b2
=> c= 5.9.k2+3.25.k2/10.9.k2-3.25.k2
=> C= k2.(5.9+3.25) / k2.(9.10-3.25)
=> C= 120/15
=> C=8
Nếu đúng tick giúp mik nha