giải thích cho mình thế nào là 2 góc phụ nhau ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Dễ thấy $x+y+z\neq 0$
Áp dụng TCDTSBN:
$\frac{1}{x+y+z}=\frac{y+x+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{y+x+1+x+z+2+x+y-3}{x+y+z}=\frac{2(x+y+z)}{x+y+z}=2$
$\Rightarrow x+y+z=\frac{1}{2}$
Có:
$\frac{x+z+2}{y}=2\Rightarrow x+z+2=2y$
$\Rightarrrow x+y+z+2=3y$
$\Rightarrow 3y=\frac{1}{2}+2=\frac{5}{2}$
$\Rightarrow y=\frac{5}{6}$
$\frac{x+y-3}{z}=2$
$\Rightarrow x+y-3=2z$
$\Rightarrow x+y+z-3=3z$
$\Rightarrow \frac{1}{2}-3=3z\Rightarrow z=\frac{-5}{6}$
$x=\frac{1}{2}-y-z=\frac{1}{2}-\frac{5}{6}-\frac{-5}{6}=\frac{1}{2}$
Thay vào giá trị $\frac{x+y+1}{x}=\frac{\frac{1}{2}+\frac{5}{6}+1}{\frac{1}{2}}=\frac{14}{3}\neq 2$ (không thỏa mãn)
Vậy không tồn tại $x,y,z$ thỏa đề.

Vì không có ai chạy cùng tốc độ nên có bao nhiêu thứ hạng chạy thì có bấy nhiêu người tham gia.
Số chạy học sinh chậm hơn Math là : 50 - 1 = 49 (học sinh )
Số học chạy nhanh hơn Math là : 50 - 1 = 49 (học sinh )
Số học sinh tham gia chạy là: 49 + 49 + 1 = 99 (người)
Kết luận:....

( 7 - \(\dfrac{1}{3}\) - 14) - ( \(\dfrac{4}{3}\) - \(\dfrac{10}{4}\)) - ( \(\dfrac{5}{4}\) - \(\dfrac{1}{3}\))
= 7 - \(\dfrac{1}{3}\) - 14 - \(\dfrac{4}{3}\) + \(\dfrac{10}{4}\) - \(\dfrac{5}{4}\) + \(\dfrac{1}{3}\)
= ( 7 - 14) - ( \(\dfrac{1}{3}\) - \(\dfrac{1}{3}\)) - \(\dfrac{4}{3}\)+ ( \(\dfrac{10}{4}\) - \(\dfrac{5}{4}\))
= -7 - 0 + \(\dfrac{4}{3}\) + \(\dfrac{5}{4}\)
= \(-\dfrac{84}{12}\) - \(\dfrac{16}{12}\) + \(\dfrac{15}{12}\)
= \(-\dfrac{85}{12}\)
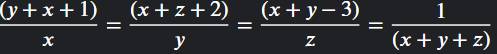
Hai góc phụ nhau là hai góc có tổng số đo bằng 90°,Ví dụ: góc 30° và góc 60° là hai góc phụ nhau.