so sánh √50+√65-√16 và √120 cái này khó quá nghĩ mãi không ra :(
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(2x-3\right)^2-\left(x-5\right)\left(4x^2-1\right)=7x+6\)
=>\(4x^2-12x+9-\left(4x^3-x-20x^2+5\right)=7x+6\)
=>\(4x^2-12x+9-4x^3+20x^2+x-5-7x-6=0\)
=>\(-4x^3+24x^2-18x-2=0\)
=>\(-4x^3+4x^2+20x^2-20x+2x-2=0\)
=>\(-4x^2\left(x-1\right)+20x\left(x-1\right)+2\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(-4x^2+20x+2\right)=0\)
=>\(\left[{}\begin{matrix}x-1=0\\-4x^2+20x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5\pm3\sqrt{3}}{2}\end{matrix}\right.\)

c) \(\dfrac{x-2}{x-1}+\dfrac{6}{x^2-x}\)
\(=\dfrac{x\left(x-2\right)}{x\left(x-1\right)}+\dfrac{6}{x\left(x-1\right)}\)
\(=\dfrac{x^2-2x+6}{x\left(x-1\right)}\)
\(=\dfrac{x^2-2x+6}{x^2-x}\)
d) \(\dfrac{x+1}{x^2-4}-\dfrac{1}{x^2+2x}\)
\(=\dfrac{x+1}{\left(x+2\right)\left(x-2\right)}-\dfrac{1}{x\left(x+2\right)}\)
\(=\dfrac{x\left(x+1\right)}{x\left(x+2\right)\left(x-2\right)}-\dfrac{x-2}{x\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+x-x+2}{x\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+2}{x\left(x^2-4\right)}\)
\(=\dfrac{x^2+2}{x^3-4x}\)

9\(x^2\) - 4 = (2\(x\) - 1).(2 - 3\(x\))
9\(x^2\) - 4 = 4\(x\) - 6\(x^2\) - 2 + 3\(x\)
9\(x^2\) - 4 - 4\(x\) + 6\(x^2\) + 2 - 3\(x\) = 0
(9\(x^2\) + 6\(x^2\)) - (4\(x\) + 3\(x\)) - (4 - 2) = 0
15\(x^2\) - 7\(x\) - 2 = 0
15\(x^2\) - 10\(x\) + 3\(x\) - 2 = 0
5\(x\)(3\(x\) - 2) + (3\(x\) - 2) = 0
(3\(x\) - 2)(5\(x\) + 1) = 0
\(\left[{}\begin{matrix}3x-2=0\\5x+1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy\(x\) \(\in\) {- \(\dfrac{1}{5}\); \(\dfrac{2}{3}\)}
\(9x^2-4=\left(2x-1\right)\left(2-3x\right)\\ \Leftrightarrow\left(3x-2\right)\left(3x+2\right)=\left(2x-1\right)\left(2-3x\right)\\ \Leftrightarrow\left(3x-2\right)\left(3x+2\right)-\left(2x-1\right)\left(2-3x\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(3x+2\right)+\left(2x-1\right)\left(3x-2\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(3x+2+2x-1\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(5x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}3x-2=0\\5x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{1}{5}\end{matrix}\right.\)

B = \(\dfrac{x^2+x-5x-5}{x^2-10x+25}\) (đk: \(x\ne5\))
B = \(\dfrac{x\left(x+1\right)-5\left(x+1\right)}{\left(x-5\right)^2}\)
B = \(\dfrac{\left(x+1\right).\left(x-5\right)}{\left(x-5\right)^2}\)
B = \(\dfrac{x+1}{x-5}\)

a:
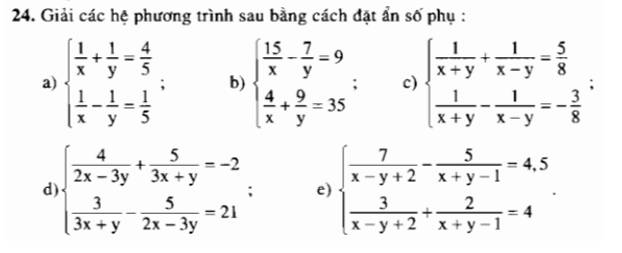
ĐKXĐ: \(x\ne0;y\ne0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\)
Hệ phương trình sẽ trở thành \(\left\{{}\begin{matrix}a+b=\dfrac{4}{5}\\a-b=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=1\\a-b=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=a-\dfrac{1}{5}=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{2}\\\dfrac{1}{y}=\dfrac{3}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{10}{3}\end{matrix}\right.\left(nhận\right)\)
b: ĐKXĐ: \(x\ne0;y\ne0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}15a-7b=9\\4a+9b=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}60a-28b=36\\60a+135b=140\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-163b=-104\\4a+9b=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{104}{163}\\a=\dfrac{4769}{652}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{4769}{652}\\\dfrac{1}{y}=\dfrac{104}{163}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{652}{4769}\\y=\dfrac{163}{104}\end{matrix}\right.\)(nhận)
c: ĐKXĐ: \(x\ne\pm y\)
Đặt \(\dfrac{1}{x+y}=a;\dfrac{1}{x-y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}a+b=\dfrac{5}{8}\\a-b=-\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=\dfrac{5}{8}-\dfrac{3}{8}=\dfrac{2}{8}=\dfrac{1}{4}\\a+b=\dfrac{5}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{1}{4}\\b=\dfrac{5}{8}-\dfrac{1}{4}=\dfrac{3}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x+y}=\dfrac{1}{4}\\\dfrac{1}{x-y}=\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=4\\x-y=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=4+\dfrac{8}{3}=\dfrac{20}{3}\\x+y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{10}{3}\\y=4-x=4-\dfrac{10}{3}=\dfrac{2}{3}\end{matrix}\right.\left(nhận\right)\)
d: ĐKXĐ: \(y\ne-3x;y\ne\dfrac{2}{3}x\)
Đặt \(\dfrac{1}{2x-3y}=a;\dfrac{1}{3x+y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}4a+5b=-2\\-5a+3b=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}20a+25b=-10\\-20a+12b=84\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}37b=84-10=74\\4a+5b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2\\a=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{2x-3y}=-3\\\dfrac{1}{3x+y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\3x+y=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\9x+3y=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=-\dfrac{1}{3}+\dfrac{3}{2}=\dfrac{7}{6}\\y=\dfrac{1}{2}-3x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{7}{66}\\y=\dfrac{1}{2}-3\cdot\dfrac{7}{66}=\dfrac{1}{2}-\dfrac{7}{22}=\dfrac{4}{22}=\dfrac{2}{11}\end{matrix}\right.\)
e: ĐKXĐ:\(x\ne y-2;x\ne-y+1\)
Đặt x-y+2=a; x+y-1=b
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}\dfrac{7}{a}-\dfrac{5}{b}=4,5\\\dfrac{3}{a}+\dfrac{2}{b}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{14}{a}-\dfrac{10}{b}=9\\\dfrac{15}{a}+\dfrac{10}{b}=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{29}{a}=29\\\dfrac{3}{a}+\dfrac{2}{b}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=1\\\dfrac{2}{b}=4-\dfrac{3}{a}=4-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y+2=1\\x+y-1=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-1\\x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)(nhận)

Nếu chia 15 dư 6 thì chắc chắn sẽ chia hết cho 3
Nếu chia 9 dư 1 thì chắc chắn sẽ không bao giờ chia hết cho 3
Do đó, hai điều này đối nghịch nhau
Từ đó suy ra, không có số tự nhiên nào chia 15 dư 6 và chia 9 dư 1
Giả sử tồn tại một số a chia cho 15 dư 6 và chia 9 dư 1 khi đó ta có:
\(\left\{{}\begin{matrix}a=15k+6\left(k\in N\right)\\15k+6-1⋮9\end{matrix}\right.\) ⇒ 15k + 6 - 1 ⋮ 3 ⇒ 15k + 5 ⋮ 3 ⇒ 3.(5k + 1) + 2 ⋮ 3
⇒ 2 ⋮ 3 (vô lí) Điều giả sử là sai.
Vậy không có số tự nhiên nào mà chia cho 15 dư 6 và chia 9 dư 1

a: Xét ΔABC có BM là phân giác
nên \(\dfrac{AM}{MC}=\dfrac{BA}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
=>\(\dfrac{AM}{3}=\dfrac{MC}{5}\)
mà AM+MC=AC=6cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{3}=\dfrac{MC}{5}=\dfrac{AM+MC}{3+5}=\dfrac{6}{8}=\dfrac{3}{4}\)
=>\(AM=3\cdot\dfrac{3}{4}=\dfrac{9}{4}\left(cm\right)\)
b: Xét ΔEBC có GQ//BC
nên \(\dfrac{EG}{EB}=\dfrac{EQ}{EC}\)
Xét ΔMBC có QI//BC
nên \(\dfrac{CI}{CM}=\dfrac{BQ}{BM}\)
Ta có: \(\widehat{ABM}=\widehat{MBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\widehat{ECB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACE}=\widehat{MBC}=\widehat{ECB}\)
Xét ΔQBC có \(\widehat{QBC}=\widehat{QCB}\)
nên ΔQBC cân tại Q
=>QB=QC
Xét ΔAMB và ΔAEC có
\(\widehat{ABM}=\widehat{ACE}\)
AB=AC
\(\widehat{BAM}\) chung
Do đó: ΔAMB=ΔAEC
=>MB=EC
mà MB=MQ+QB
và EC=EQ+QC
và QB=QC
nên MQ=EQ
\(\dfrac{EG}{EB}+\dfrac{CI}{CM}=\dfrac{EQ}{EC}+\dfrac{BQ}{BM}=1-\dfrac{CQ}{CE}+\dfrac{BQ}{BM}\)
\(=1-\dfrac{BQ}{BM}+\dfrac{BQ}{BM}=1\)

\((z-3)^2-(x-2y)^2\\=[(z-3)-(x-2y)][(z-3)+(x-2y)]\\=(z-3-x+2y)(z-3+x-2y)\)
\(\left(z-3\right)^2-\left(x-2y\right)^2\)
\(=\left[\left(z-3\right)-\left(x-2y\right)\right]\left[\left(z-3\right)+\left(x-2y\right)\right]\)
\(=\left(z-3-x+2y\right)\left(z-3+x-2y\right)\)
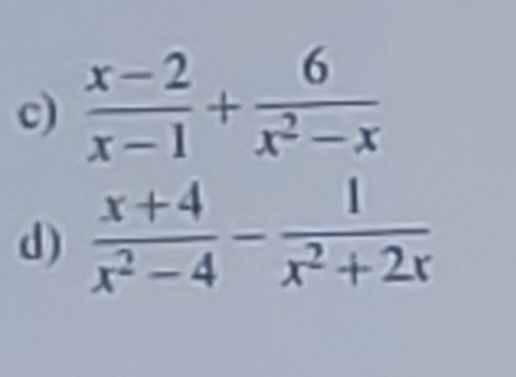
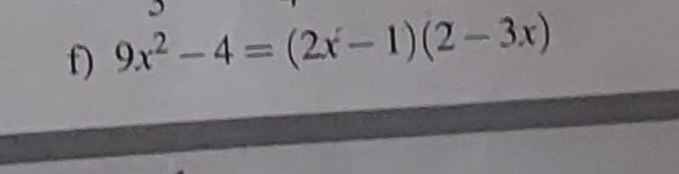
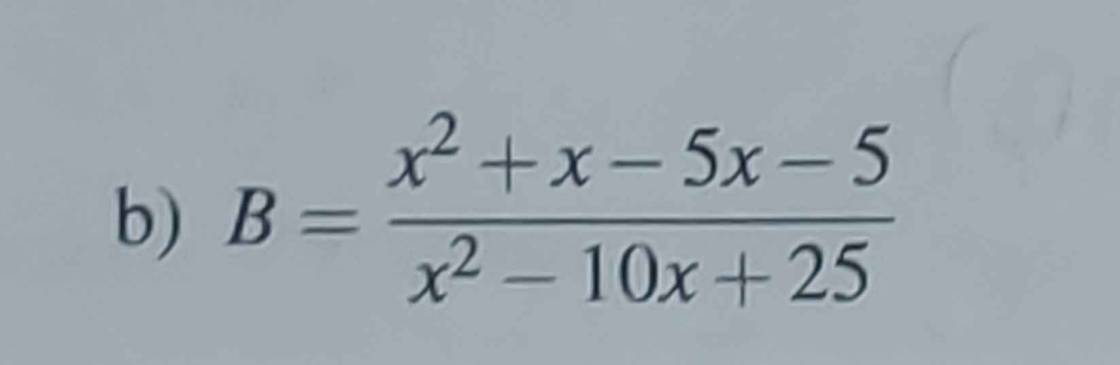

`#3107.101107`
Ta có: `\sqrt{50} + \sqrt{65} - \sqrt{16} > \sqrt{49} + \sqrt{64} - \sqrt{16} = 7 + 8 + 4 = 19`
Mà `\sqrt{120} < \sqrt{361} (= 19)`
`\Rightarrow \sqrt{50} + \sqrt{65} - \sqrt{16} > \sqrt{120}`
Bảo mình chép mạng thì lên mạng mà tìm xem có đáp án dở ra ngay trước mặt không? Mà biết thì cũng kệ bạn chứ ai hỏi. Người tiếp xúc qua 2 3 cái màn hình mà làm như kiểu sống dưới gầm dường người khác vậy bạn, bạn nghĩ bạn đủ tư cách để buộc tội mình á? Xin lỗi nha, tới khi nào mình thấy bạn có danh phận ảnh hưởng, có bằng chứng rõ ràng thì lại mở miệng. Kể cả người khác sống trong nhà mình họ còn chưa chắc chắn, bạn lấy điều gì mà tự tin với mấy câu nói vu vơ vậy thế :D? Mà việc mình làm tự bản thân mình cũng biết, chưa cần đến lượt bạn phải nói. Sau bớt bình luận vô duyên giúp, ảnh hưởng noti người khác lắm. Cũng chả ai cần đâu. Đúng vô duyên luôn.