Cho tam giác ABC, lấy các điểm D,E theo thứ tự thuộc tia đối của các tia BA, CA sao cho BD = CE = BC. Gọi O là giao điểm của BE và CD. Qua O vẽ đường thẳng song song với tia phân giác của góc A, đường thẳng này cắt AC ở K.
Chứng minh AB = CK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DT
Đinh Thị Huyền
Giáo viên
15 tháng 6
Đúng(4)
15 tháng 6
a: Xét tứ giác ABMD có
AD//BM
AB//MD
Do đó: ABMD là hình bình hành
=>AD=BM; AB=MD
Xét tứ giác AEMC có
AE//MC
AC//ME
Do đó: AEMC là hình bình hành
=>AE=MC; ME=AC
Ta có: AE+AD=DE
BM+MC=BC
mà AD=BM và MC=AE
nên DE=BC
Xét ΔABC và ΔMDE có
AB=MD
BC\DE
AC=ME
Do đó: ΔABC=ΔMDE
b: Ta có: AEMC là hình bình hành
=>AM cắt EC tại trung điểm của mỗi đường(1)
Ta có: ABMD là hình bình hành
=>AM cắt BD tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AM,EC,BD đồng quy
14 tháng 6
\(x^3+6x^2+11x+6\)
\(=x^3+x^2+5x^2+5x+6x+6\)
\(=x^2\left(x+1\right)+5x\left(x+1\right)+6\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+5x+6\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\)
B
1
KV
14 tháng 6
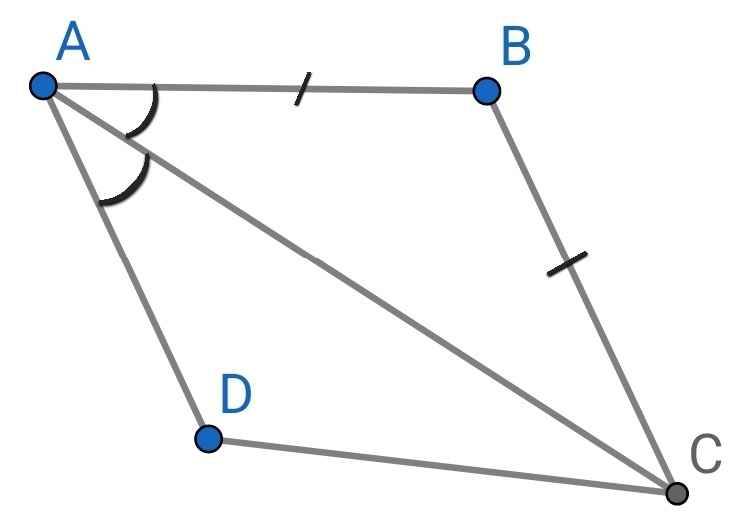
∆ABC có:
AB = BC (gt)
⇒ ∆ABC cân tại B
⇒ ∠BAC = ∠BCA (1)
Do AC là tia phân giác của ∠BAD (gt)
⇒ ∠DAC = ∠BAC (2)
Từ (1) và (2) ⇒ ∠BCA = ∠DAC
Mà ∠BCA và ∠DAC là hai góc so le trong
⇒ BC // AD
⇒ ABCD là hình thang
KV
14 tháng 6
a) Do x là số nguyên nên 2x + 1 là số nguyên lẻ
Để phân thức đã cho nhận giá trị nguyên thì 2 ⋮ (2x + 1)
⇒ 2x + 1 ∈ Ư(2) = {-1; 1}
⇒ 2x ∈ {-2; 0}
⇒ x ∈ {-1; 0}
Vậy có 2 giá trị nguyên của x thỏa mãn yêu cầu đề bài
b) Ta có:
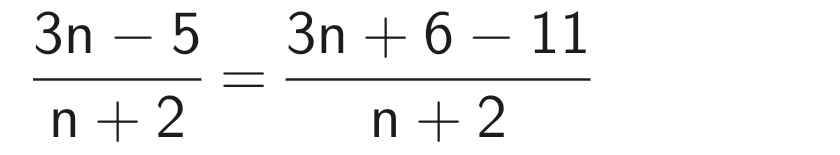
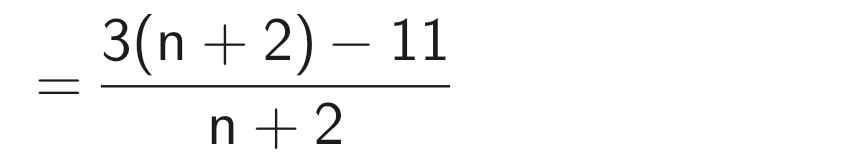
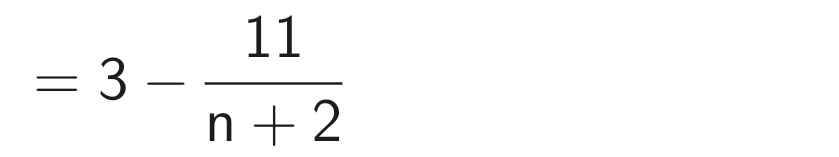
Để phân thức đã cho nhận giá trị nguyên thì 11 ⋮ (n + 2)
⇒ n + 2 ∈ Ư(11) = {-11; -1; 1; 11}
⇒ n ∈ {-13; -3; -1; 9}
Vậy có 4 giá trị nguyên của n thỏa mãn yêu cầu đề bài
KL
1
KV
14 tháng 6
|3x - 2| = 4x + 1
|3x - 2| = 3x - 2 khi x ≥ 2/3
|3x - 2| = 2 - 3x khi x < 2/3
*) Với x ≥ 2/3, ta có:
|3x - 2| = 4x + 1
3x - 2 = 4x + 1
3x - 4x = 1 + 2
-x = 3
x = -3 (loại)
*) Với x < 2/3, ta có:
|3x - 2| = 4x + 1
2 - 3x = 4x + 1
-3x - 4x = 1 - 2
-7x = -1
x = 1/7 (nhận)
Vậy phương trình đã cho có 1 nghiệm
TL
1
14 tháng 6
Ta có hệ phương trình: a^3 - 3ab^2 = 2,b^3 - 3a^2b = -11
Cộng hai phương trình với nhau ta được:
a^3 - 3ab^2 + b^3 - 3a^2b
= 2 - 11,(a^3 + b^3) - 3ab(a + b)
= -9,(a + b)(a^2 - ab + b^2) - 3ab(a + b)
= -9,(a + b)(a^2 - ab + b^2 - 3ab)
= -9,(a + b)(a^2 - 4ab + b^2) = -9
Ta cần tìm giá trị của a^2 + b^2. Ta có:,(a + b)^2 = a^2 + b^2 + 2ab
Vậy:,a^2 + b^2 = (a + b)^2 - 2ab
Ta có:,a^3 - 3ab^2 = 2,b^3 - 3a^2b = -11
Cộng hai phương trình ta được:
a^3 + b^3 - 3ab(a + b)
= -9,(a + b)(a^2 - ab + b^2) - 3ab(a + b)
= -9,(a + b)(a^2 - ab + b^2 - 3ab)
= -9,(a + b)(a^2 - 4ab + b^2) = -9
Thay a^2 - 4ab + b^2 = -9 vào phương trình (a + b)(a^2 - 4ab + b^2) = -9 ta được:
(a + b)(-9) = -9,a + b = 1
Thay a + b = 1 vào công thức a^2 + b^2 = (a + b)^2 - 2ab
Ta được:,a^2 + b^2 = 1^2 - 2ab,a^2 + b^2 = 1 - 2ab
Vậy để tính a^2 + b^2, chúng ta cần tìm giá trị của ab.
Thay a + b = 1 vào a^3 - 3ab^2 = 2 ta được:
a^3 - 3ab^2 =
2,a^3 - 3a(1 - a)^2
= 2,a^3 - 3a(1 - 2a + a^2)
= 2,a^3 - 3a + 6a^2 - 3a^3
= 2,-2a^3 + 6a^2 - 3a - 2
= 0,2a^3 - 6a^2 + 3a + 2
= 0,2(a^3 - 3a^2 + 3a - 1)
= 0,2(a - 1)^3 = 0
Vậy a = 1 hoặc a = b
Nếu a = 1, ta có:
1 - 3b^2 = 2,-3b^2 = 1,b^2 = -1, không có giá trị thực cho b.
Nếu a = b, ta có:,a^3 - 3a^3 = 2,-2a^3 = 2,a^3 = -1,a = -1
Vậy a = -1, b = -1
Thay a = -1, b = -1 vào a^2 + b^2 = 1 - 2ab ta được:
a^2 + b^2 = 1 - 2(-1)(-1) = 1 - 2 = -1
Vậy kết quả là a^2 + b^2 = -1.
14 tháng 6
\(A=2\left(x^6+y^6\right)-3\left(x^4+y^4\right)\)
\(=2\left[\left(x^2+y^2\right)^3-3x^2y^2\left(x^2+y^2\right)\right]-3\left[\left(x^2+y^2\right)^2-2x^2y^2\right]\)
\(=2\left[1-3x^2y^2\right]-3\left(1-2x^2y^2\right)\)
\(=2-6x^2y^2-3+6x^2y^2=-1\)
14 tháng 6
a: Số tiền trả 1 giờ làm theo quy định là:
2000000:40=50000(đồng)
b: Số tiền trả cho 1 giờ làm thêm là:
50000x(1+50%)=75000(đồng)
Tổng số tiền Bình được trả là:
2000000+75000*5=2375000(đồng)