giúp mik nhé, mik cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: \(\widehat{xOy}=\widehat{mOn}\)(hai góc đối đỉnh)
mà \(\widehat{xOy}=50^0\)
nên \(\widehat{mOn}=50^0\)
Ta có: \(\widehat{xOy}+\widehat{mOy}=180^0\)(hai góc kề bù)
=>\(\widehat{mOy}+50^0=180^0\)
=>\(\widehat{mOy}=130^0\)
Ta có: \(\widehat{xOn}=\widehat{mOy}\)(hai góc đối đỉnh)
mà \(\widehat{mOy}=130^0\)
nên \(\widehat{xOn}=130^0\)
b: Oa là phân giác của góc xOy
=>\(\widehat{yOa}=\dfrac{\widehat{xOy}}{2}=25^0\)
Ta có: Ob là phân giác của góc yOm
=>\(\widehat{yOb}=\dfrac{\widehat{yOm}}{2}=65^0\)
Ta có: \(\widehat{aOb}=\widehat{aOy}+\widehat{bOy}=25^0+65^0=90^0\)

a: Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
b: ΔBAE=ΔBDE
=>\(\widehat{BAE}=\widehat{BDE}\)
=>\(\widehat{BDE}=90^0\)
=>DE\(\perp\)BC tại D
XétΔBHF vuông tại H và ΔBHC vuông tại H có
BH chung
\(\widehat{HBF}=\widehat{HBC}\)
Do đó ΔBHF=ΔBHC
c: Xét ΔBFC có
BH,CA là các đường cao
BH cắt CA tại E
Do đó: E là trực tâm của ΔBFC
=>FE\(\perp\)BC
mà DE\(\perp\)BC
và FE,DE có điểm chung là E
nên F,E,D thẳng hàng

\(d.\dfrac{59-x}{41}+\dfrac{57-x}{43}=\dfrac{41-x}{59}+\dfrac{43-x}{57}\\ \left(\dfrac{59-x}{41}+1\right)+\left(\dfrac{57-x}{43}+1\right)=\left(\dfrac{41-x}{59}+1\right)+\left(\dfrac{43-x}{57}+1\right)\\ \dfrac{100-x}{41}+\dfrac{100-x}{43}=\dfrac{100-x}{59}+\dfrac{100-x}{57}\\ \left(100-x\right)\left(\dfrac{1}{41}+\dfrac{1}{43}-\dfrac{1}{59}-\dfrac{1}{57}\right)=0\\ 100-x=0\\ x=100\)

bài 4:
\(C=\left(1+\dfrac{1}{1\cdot3}\right)\left(1+\dfrac{1}{2\cdot4}\right)\cdot...\cdot\left(1+\dfrac{1}{98\cdot100}\right)\)
\(=\left(1+\dfrac{1}{2^2-1}\right)\left(1+\dfrac{1}{3^2-1}\right)\cdot...\cdot\left(1+\dfrac{1}{99^2-1}\right)\)
\(=\dfrac{2^2}{2^2-1}\cdot\dfrac{3^2}{3^2-1}\cdot...\cdot\dfrac{99^2}{99^2-1}\)
\(=\dfrac{2\cdot3\cdot...\cdot99}{1\cdot2\cdot3\cdot...\cdot98}\cdot\dfrac{2\cdot3\cdot...\cdot99}{3\cdot4\cdot...\cdot100}=\dfrac{99}{1}\cdot\dfrac{2}{100}=\dfrac{99}{50}\)
Bài 5:
\(B=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{205}}{\dfrac{204}{1}+\dfrac{203}{2}+...+\dfrac{1}{204}}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{205}}{\left(1+\dfrac{203}{2}\right)+\left(1+\dfrac{202}{3}\right)+...+\left(\dfrac{1}{204}+1\right)+1}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{205}}{\dfrac{205}{2}+\dfrac{205}{3}+...+\dfrac{205}{205}}=\dfrac{1}{205}\)

Bài 5
Ta có:
\(x^2-x-6=\left(x-3\right)\left(x+2\right)\) và đa thức chia bậc 2 nên dư là \(ax+b\)
Vậy \(f\left(x\right)=\left(x-3\right)\left(x+2\right)\left(x^2+4\right)+ax+b\)
Theo định lí Bezout, dư trong phép chia \(f\left(x\right)\) cho \(x-3\) là \(f\left(3\right)=21\) cho \(x+2\) là \(f\left(-2\right)=4\) nên ta có: \(\left\{{}\begin{matrix}3a+b=21\\-2a+b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=5\\b=6\end{matrix}\right.\)
Đa thức cần tìm là \(\left(x+2\right)\left(x-3\right)\left(x^2+4\right)+5x+6=x^4-x^3-2x^2+x-18\)
Bài 4:
\(2n^2+6n-7⋮n-2\)
=>\(2n^2-4n+10n-20+13⋮n-2\)
=>\(13⋮n-2\)
=>\(n-2\in\left\{1;-1;13;-13\right\}\)
=>\(n\in\left\{3;1;15;-11\right\}\)

\(a.\dfrac{\dfrac{3}{4}-\dfrac{3}{5}+\dfrac{3}{7}+\dfrac{3}{13}}{\dfrac{11}{4}-\dfrac{11}{5}+\dfrac{11}{7}+\dfrac{11}{13}}:\dfrac{\dfrac{3}{5}-\dfrac{3}{8}+\dfrac{3}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}\\ =\dfrac{3\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{11}\right)}{11\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{11}\right)}:\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}\\ =\dfrac{3}{11}:\dfrac{3}{7}\\ =\dfrac{3}{11}\cdot\dfrac{7}{3}\\ =\dfrac{7}{11}\\ b.\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{19\cdot21}\\ =\dfrac{1}{2}\cdot\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{19\cdot21}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{21}\right)\\ =\dfrac{1}{2}\cdot\dfrac{20}{21}=\dfrac{10}{21}\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=BC^2-AB^2=20^2-12^2=256=16^2\)
=>AC=16(cm)
b: Xét ΔHID vuông tại H và ΔHBA vuông tại H có
HI=HB
HD=HA
Do đó: ΔHID=ΔHBA
=>DI=BA
ΔHID=ΔHBA
=>\(\widehat{HDI}=\widehat{HAB}\)
=>DI//AB
c: Ta có: DI//AB
AB\(\perp\)AC
Do đó: DI\(\perp\)AC
Xét ΔCAD có
DI,CH là các đường cao
DI cắt CH tại I
Do đó: I là trực tâm của ΔCAD
=>AI\(\perp\)CD
d: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot20=12\cdot16=192\)
=>AH=192/20=9,6(cm)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB=\sqrt{12^2-9,6^2}=7,2\left(cm\right)\)
=>AH>HB
mà AD=2AH và BI=2BH
nên AD>BI


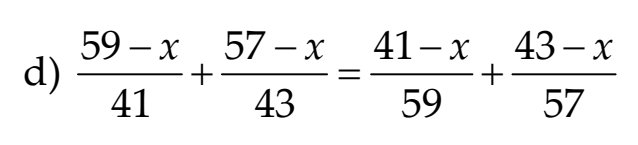
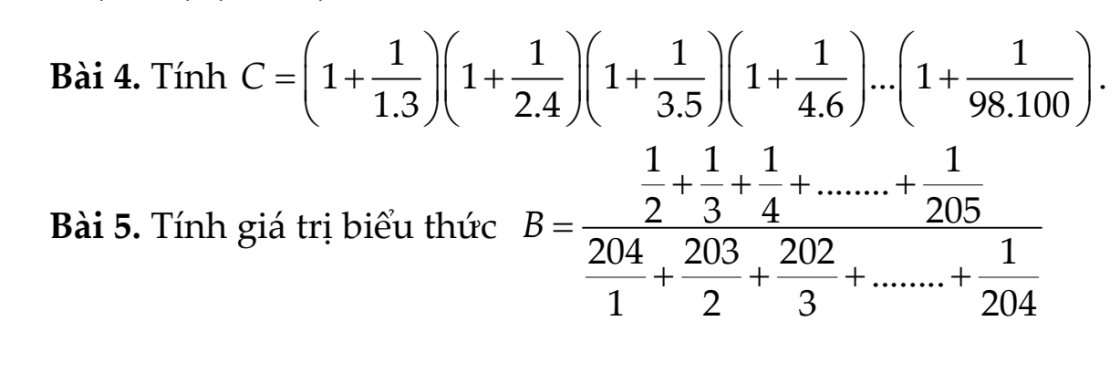



a: a\(\perp\)HK
b\(\perp\)HK
Do đó: a//b
b: Ta có: \(\widehat{BAH}+45^0=180^0\)
=>\(\widehat{BAH}=180^0-45^0=135^0\)
Ta có: a//b
=>\(\widehat{BAH}+\widehat{ABK}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{ABK}+135^0=180^0\)
=>\(\widehat{ABK}=45^0\)