Gọi số học sinh của lớp 7A,7B,7C lần lượt là a,b,c ( \(a,b,c\in\) N^* )

Theo đề bài ta có :

a,b,c tỉ lệ với 3,5,7 

= > \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\) và a + b + c = 105

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{105}{15}=7\)

\(\dfrac{a}{3}=7=>a=21\)

\(\dfrac{b}{5}=7=>b=35\)

\(\dfrac{c}{7}=7=>c=49\)

Vậy số học sinh của các lớp 7A,7B, 7C lần lượt là 21 , 35 , 49 

a, Xét tam giác \(\Delta ABH\) và \(\Delta ACH\) có :

\(HB=HC\left(gt\right)\)

\(\widehat{B}=\widehat{C}\left(gt\right)\)

\(AB=AC\left(gt\right)\)

= > \(\Delta ABH=\Delta ACH\left(c-g-c\right)\)

b, M là trung điểm của cạnh AC = > MA = 1/2 AC ( 1 )

 N là trung điểm của cạnh AB = > NA = 1/2 AB  ( 2 )

Từ ( 1 ) , ( 2 ) = > MA = NA   ( Do AB = AC )

Mà tam giác ABH = tam giác ACH ( câu a, )

= > \(\widehat{BAH}=\widehat{CAH}\) ( 2 góc tương ứng )

Xét \(\Delta ANH\) và \(\Delta AMH\) có :

\(AN=AM\left(cmt\right)\)

\(\widehat{BAH}=\widehat{CAH}\left(cmt\right)\)

AH chung 

= > \(\Delta ANH=\Delta AMH\left(c-g-c\right)\)

= > HN = HM ( 2 cạnh tương ứng )

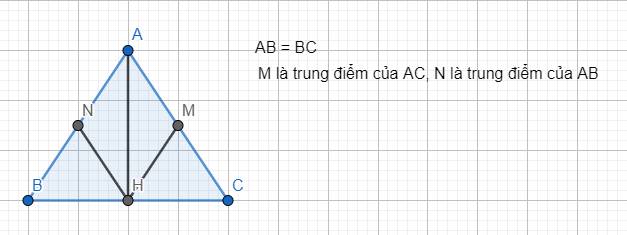
a) Xét hai tam giác ABH và ACH ta có:

- AB = AC (vì ABC là tam giác cân)

- HB = HC (vì H là trung điểm của BC)

- \(\widehat{B}=\widehat{C}\) (vì ABC là tam giác cân)

Vậy \(\Delta ABH=\Delta ACH\) (c.g.c)

b) Xét hai tam giác NBH và MCH ta có:

- NB = MC (vì AB = AC, M là trung điểm của AC và N là trung điểm của AB)

- HB = HC (đã chứng minh trên)

- \(\widehat{B}=\widehat{C}\) (đã chứng minh trên)

Suy ra \(\Delta NBH=\Delta MCH\) (c.g.c)

Khi đó HN = HM (vì hai cạnh tương ứng)

Từ tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{3x+2}{3}=\dfrac{2y-6}{9}=\dfrac{\left(3x+2\right)+\left(2y-6\right)}{3+9}=\dfrac{3x+2y-4}{12}=\dfrac{3x+2y-4}{6x}\)

Suy ra 6x = 12 <=> x = 12 : 6 = 2

Khi đó \(\dfrac{3x+2}{3}=\dfrac{3\cdot2+2}{3}=\dfrac{8}{3}\)

Suy ra \(\dfrac{2y-6}{9}=\dfrac{8}{3}\Leftrightarrow2y-6=\dfrac{8\cdot9}{3}=24\)

\(\Leftrightarrow2y=24+6=30\Leftrightarrow y=30:2=15\)

Vậy x = 2; y = 15

minh trang là nữ hay nam

F(\(x\)) = -2\(x\)⁴ + 3\(x^3\) - 4\(x\) + 2\(x^4\) - \(x^2\) - 3\(x^3\) - \(x\) + 1

F(\(x\)) = ( -2\(x^4\)+2\(x^4\)) + (3\(x^3\) - 3\(x^3\)) -(4\(x\) + \(x\)) + 1

F(\(x\)) = 0 + 0 - 5\(x\) + 1

F(\(x\)) = - 5\(x\) + 1

\(f\left(x\right)=-2x^4+3x^3-4x+2x^4-x^2-3x^3-x+1\)

\(f\left(x\right)=-2x^4+2x^4+3x^3-3x^3-4x-x-x^2+1\)

\(f\left(x\right)=-5x-x^2+1\)

Trên là 3 xuống thành 2 rồi :v 

Chỗ :  \(-x^2\) 

` P(x) = x^3-2x^2+x-2`

`Q(x) = 2x^3 - 4x^2+ 3x – 5​​​​6`

a) `P(x) -Q(x)`

`= x^3-2x^2+x-2 - 2x^3 +4x^2 -3x +56`

`=(x^3-2x^3) +(4x^2-2x^2) +(x-3x) +(-2+56)`

`= -x^2 +2x^2 -2x +54`

b) Thay `x=2` vào `P(x)` ta đc

`P(2) = 2^3 -2*2^2 +2-2`

`= 8-8+2-2 =0`

Vậy chứng tỏ `x=2` là nghiệm của đa thức `P(x)`

Thay `x=2` vào `Q(x)` ta đc

`Q(2) = 2*2^3 -4*2^2 +3*2-56`

`=16 -16+6-56`

`= -50`

Vậy chứng tỏ `x=2` là ko nghiệm của đa thức `Q(x)`

Đổi:6h=360 phút
Ta có : 15 người đào xog con muong trong 6h
            25 người đào xog con muong x h
Vì số người và thòi gian đào là 2 đại lượng tỉ  lệ nghịch
15.360=25.x
=>5400=25.x
=>x=5400:25
=>x=216 (phút)
Đổi 216 phút = 3,6h
vậy giảm số h là 6-3,6=2,4 (giò)

 

hoi chậm xl bạn nha

Câu `3`

`1,`

ADTC dãy tỉ số bằng nhau ta có :

`x/2 = y/3= (x-y)/(2-3)=9/(-1)=-9`

`=>x/2=-9=>x=-9.2=-18`

`=>y/3=-9=>y=-9.3=-27`

`2,`

ADTC dãy tỉ số bằng nhau ta có :

`x/3 = y/5 = (x+y)/(3+5)= 32/8=4`

`=>x/3=4=>x=4.3=12`

`=.y/5=4=>y=4.5=20`

`3,`

ADTC dãy tỉ số bằng nhau ta có :

`x/3 = y/5 = (x+y)/(3+5)=24/8=3`

`=>x/3=3=>x=3.3=9`

`=>y/5=3=>y=3.5=15`

a, M(\(x\) )+N(\(x\)) = 3\(x^4\) - 2\(x\)³ + 5\(x^2\) - \(4x\)+ 1 + ( -3\(x^4\) + 2\(x^3\)- 3\(x^2\)+ 7\(x\) + 5)

M(\(x\)) + N(\(x\)) = ( 3\(x^4\)- 3\(x^4\))+( -2\(x^3\) + 2\(x^3\))+(5\(x^2\) - 3\(x^2\))+( 7\(x-4x\)) +(1+5)

M(\(x\)) + N(\(x\)) = 0 + 0 + 2\(x^2\) + 3\(x\) + 6

M(\(x\)) + N(\(x\)) = 2\(x^2\) + 3\(x\) + 6

b, P(\(x\)) = M(\(x\)) + N(\(x\)) = 2\(x^2\) + 3\(x\) + 6

P(-2) = 2.(-2)² + 3.(-2) + 6 = 8 - 6 + 6 = 8