1) sin35⁰ = cos(90⁰ - 35⁰) = cos55⁰

Vậy sin35⁰ = cos55⁰

tan35⁰ = cot(90⁰ - 35⁰) = cot55⁰

Vậy tan35⁰ = cot55⁰

2) ∆ABC vuông tại A (gt)

⇒ AB = BC.cosB

= 20.cos36⁰

≈ 16,18 (cm)

Gọi vận tốc lúc về của người đó là x(km/h)

(Điều kiện: x>0)

Vận tốc lúc đi là x+10(km/h)

Thời gian người đó đi từ A đến B là \(\dfrac{60}{x+10}\left(giờ\right)\)

Thời gian người đó đi từ B về A là \(\dfrac{60}{x}\left(giờ\right)\)

Thời gian về nhiều hơn thời gian đi là 30p=0,5 giờ nên ta có:

\(\dfrac{60}{x}-\dfrac{60}{x+10}=0,5\)

=>\(\dfrac{60x+600-60x}{x\left(x+10\right)}=0,5\)

=>\(x\left(x+10\right)=\dfrac{600}{0,5}=1200\)

=>\(x^2+10x-1200=0\)

=>(x+40)(x-30)=0

=>\(\left[{}\begin{matrix}x+40=0\\x-30=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-40\left(loại\right)\\x=30\left(nhận\right)\end{matrix}\right.\)

Vậy: Vận tốc lúc về của người đó là 30km/h

a) ĐKXĐ: x ≠ -5

Phương trình đã cho trở thành:

(x + 6).2 + 3.(x + 5) = 2.2(x + 5)

2x + 12 + 3x + 15 = 4x + 20

5x - 4x = 20 - 12 - 15

x = -7 (nhận)

Vậy S = {-7}

b) x + 3y = -2

x = -2 - 3y (1)

5x + 8y = 11 (2)

Thế (1) vào (2), ta được:

5(-2 - 3y) + 8y = 11

-10 - 15y + 8y = 11

-7y = 11 + 10

-7y = 21

y = 21 : (-7)

y = -3

Thế y = -3 vào (1), ta được:

x = -2 - 3.(-3) = 7

Vậy S = {(7; -3)}

a) Nhiệt độ t (⁰C) tuần tới tại Tokyo là:

t > -5

b) Gọi x (tuổi) là tuổi của người điều khiển xe máy điện. Ta có bất đẳng thức:

x ≥ 16

c) Gọi z (đồng) là mức lương tối thiểu trong một giờ làm việc của người lao động. Ta có bất đẳng thức:

z ≥ 20000

d) y là số dương nên ta có bất đẳng thức:

y > 0

a, t>5

b,x≥16

c,mức lương tối thiểu≤20 000đ

d, y>0

`DE = DB . sinB = 10. sin70^o ~~ 9,4 (m) `

`=> AF ~~ 15 - 9,4~~ 5,6 (m) `

`ΔAFD` vuông tại `F `

`=> AD = sqrt{AF^2 + DF^2} = sqrt{AF^2 + EC^2} = sqrt{5,6^2 + 13^2} ~~14,15 (m)`

Vậy ....

Bài 1:

a: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)

nên BFEC là tứ giác nội tiếp đường tròn đường kính BC

=>B,F,E,C cùng thuộc một đường tròn

b: Xét (O) có

\(\widehat{CNM}\) là góc nội tiếp chắn cung CM

\(\widehat{CBM}\) là góc nội tiếp chắn cung CM

Do đó: \(\widehat{CNM}=\widehat{CBM}\)

mà \(\widehat{CBM}=\widehat{HFE}\)(BFEC nội tiếp)

nên \(\widehat{HFE}=\widehat{HNM}\)

mà hai góc này là hai góc ở vị trí đồng vị

nên FE//MN

c: Gọi Ax là tiếp tuyến tại A của (O)

Xét (O) có

\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC

\(\widehat{ABC}\) là góc nội tiếp chắn cung AC

Do đó: \(\widehat{xAC}=\widehat{ABC}\)

mà \(\widehat{ABC}=\widehat{AEF}\left(=180^0-\widehat{FEC}\right)\)

nên \(\widehat{xAC}=\widehat{AEF}\)

mà hai góc này là hai góc ở vị trí so le trong

nên EF//Ax

mà Ax\(\perp\)OA

nên OA\(\perp\)EF

d: Xét (O) có

ΔABK nội tiếp

AK là đường kính

Do đó: ΔABK vuông tại B

=>BA\(\perp\)BK

mà CH\(\perp\)BA

nên CH//BK

Xét (O) có

ΔACK nội tiếp

AK là đường kính

Do đó: ΔACK vuông tại C

=>CA\(\perp\)CK

mà BH\(\perp\)AC

nên BH//CK

Xét tứ giác BHCK có

BH//CK

BK//CH

Do đó: BHCK là hình bình hành

=>BC cắt HK tại trung điểm của mỗi đường

mà I là trung điểm của BC

nên I là trung điểm của HK

=>H,I,K thẳng hàng

Xét ΔKAH có

I,O lần lượt là trung điểm của KH,KA

=>IO là đường trung bình của ΔKAH

=>AH=2IO

e: Xét (O) có

\(\widehat{MCA};\widehat{MBA}\) là góc nội tiếp chắn cung MA

Do đó: \(\widehat{MCA}=\widehat{MBA}\)

mà \(\widehat{MBA}=\widehat{ACN}\left(=90^0-\widehat{BAC}\right)\)

nên \(\widehat{MCA}=\widehat{NCA}\)

=>CA là phân giác của góc CMN

Xét ΔCHM có

CA là đường cao

CA là đường phân giác

Do đó: ΔCHM cân tại C

ΔCHM cân tại C

mà CA là đường cao

nên CA là đường trung trực của HM

=>H đối xứng M qua AC

Bài 2: 

a: Xét (O) có

\(\widehat{BAE}\) là góc nội tiếp chắn cung BE

\(\widehat{CAE}\) là góc nội tiếp chắn cung CE

\(\widehat{BAE}=\widehat{CAE}\)(AE là phân giác của góc BAC)

Do đó: \(sđ\stackrel\frown{BE}=sđ\stackrel\frown{CE}\)

=>EB=EC

=>ΔEBC cân tại E

b: EG=EC

=>E là trung điểm của GC

Xét ΔGBC có

BE là đường trung tuyến

\(BE=\dfrac{GC}{2}\)

Do đó: ΔGBC vuông tại B

=>GB\(\perp\)BC tại B

=>GB là tiếp tuyến của đường tròn đường kính BC

c: Xét (O) có

\(\widehat{BAE};\widehat{BCE}\) là các nội tiếp cùng chắn cung BE

Do đó: \(\widehat{BAE}=\widehat{BCE}\)

Xét ΔDAB và ΔDCE có

\(\widehat{DAB}=\widehat{DCE}\)

\(\widehat{ADB}=\widehat{CDE}\)(hai góc đối đỉnh)

Do đó: ΔDAB~ΔDCE

=>\(\dfrac{DA}{DC}=\dfrac{DB}{DE}\)

=>\(DA\cdot DE=DB\cdot DC\)

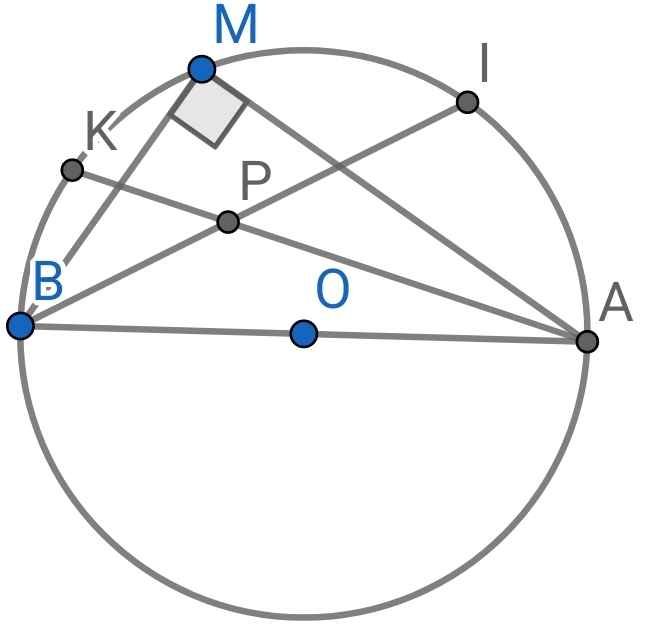
a) Do MA ⊥ MB (gt)

⇒ ∠MAB = 90⁰

⇒ M, A, B thuộc đường tròn đường kính AB

Mà M, A, B thuộc (O)

⇒ O là trung điểm của AB

⇒ A, O, B thẳng hàng

b) Do I là điểm chính giữa của cung nhỏ MA (gt)

⇒ sđ cung AI = sđ cung MI

⇒ ∠ABI = ∠MBI (hai góc nội tiếp chắn hai cung bằng nhau)

⇒ BI là tia phân giác của ∠ABM

Do K là điểm chính giữa của cung MB (gt)

⇒ sđ cung BK = sđ cung MK

⇒ ∠BAK = ∠MAK (hai góc nội tiếp chắn hai cung bằng nhau)

⇒ AK là tia phân giác của ∠BAM

Mà P là giao điểm của AK và BI (gt)

⇒ P là giao điểm của ba đường phân giác của ∆MAB

⇒ P là tâm đường tròn nội tiếp ∆MAB

a.

Do \(OM=OA=R\Rightarrow\Delta OAM\) cân tại O

\(\Rightarrow\widehat{OAM}=\widehat{OMA}\Rightarrow\widehat{AOM}=180^0-\left(\widehat{OAM}+\widehat{OMA}\right)=180^0-2\widehat{OMA}\)

Tương tự, \(\Delta OBM\) cân tại O

\(\Rightarrow\widehat{BOM}=180^0-2\widehat{OMB}\)

\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2\left(\widehat{OMA}+\widehat{OMB}\right)\)

\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2.\widehat{AMB}=360^0-2.90^0=180^0\)

\(\Rightarrow A,O,B\) thẳng hàng

b.

Do I là điểm chính giữa cung MA \(\Rightarrow sđ\stackrel\frown{AI}=sđ\stackrel\frown{MI}\Rightarrow\widehat{ABI}=\widehat{MBI}\)

\(\Rightarrow BI\) là tia phân giác góc \(\widehat{ABM}\) (1)

Do K là điểm chính giữa cung MB \(\Rightarrow sđ\stackrel\frown{MK}=sđ\stackrel\frown{BK}\Rightarrow\widehat{MAK}=\widehat{BAK}\)

\(\Rightarrow AK\) là tia phân giác góc \(\widehat{MAB}\) (2)

(1);(2) \(\Rightarrow P\) là giao điểm 2 đường phân giác trong của tam giác MAB

\(\Rightarrow P\) là tâm đường tròn nội tiếp tam giác MAB

    Giải Phương trình bậc nhất một ẩn, Olm hướng dẫn các em làm từng bước cụ thể như sau:

Bước 1: Thu gọn biểu thức nếu có thể theo quy tắc thực hiện phép tính.

Bước 2: Chuyển vế đổi dấu (chuyển tất cả các thành phần có chứa ẩn về một vế, vế kia là hằng số)

Bước 3: Tìm được ẩn theo theo quy tắc tìm thành phần chưa biết của phép tính.

Bước 4 kết luận.