 SOS cần gấp
SOS cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3n+5⋮n-3\)
=>\(3n-9+14⋮n-3\)
=>\(14⋮n-3\)
=>\(n-3\in\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
=>\(n\in\left\{4;2;5;1;10;-4;17;-11\right\}\)
mà n>=0
nên \(n\in\left\{4;2;5;1;10;17\right\}\)
(3n + 5) ⋮ (n - 3) đk n \(\in\) N
3(n - 3) + 14 ⋮ n - 3
14 ⋮ n - 3
n - 3 \(\in\) Ư(14) = {-14; -7; -2; -1; 1; 2; 7; 14}
n \(\in\) {-11; -4; 1; 2; 4; 5; 10; 17}
Vì n \(\in\) N nên n \(\in\) { 1; 2; 4; 5; 10; 17}

1: \(\left(2x+1\right)^2-2\left(2x+1\right)\left(3-x\right)+\left(x-3\right)^2\)
\(=\left(2x+1\right)^2+2\left(2x+1\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+1+x-3\right)^2=\left(3x-2\right)^2=9x^2-12x+4\)
2: \(\left(x-1\right)^3-\left(x+1\right)\left(x^2-x+1\right)-\left(1-3x\right)\left(1+3x\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+1\right)-\left(1-9x^2\right)\)
\(=x^3-3x^2+3x-1-x^3-1-1+9x^2\)
\(=6x^2+3x-3\)
3: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x-1\right)\left(x+1\right)+3x\)
\(=x^3+8-x\left(x^2-1\right)+3x\)
\(=x^3+8-x^3+x+3x=4x+8\)
4: \(\left(3x-2\right)^2-3\left(x-4\right)\left(x+4\right)+\left(x-3\right)^2-\left(x+1\right)\left(x^2-x+1\right)\)
\(=9x^2-12x+4-3\left(x^2-16\right)+x^2-6x+9-\left(x^3+1\right)\)
\(=10x^2-18x+13-3x^2+48-x^3-1\)
\(=-x^3+7x^2-18x+12\)
5: \(\left(x+1\right)^2-\left(x-1\right)^2-3\left(x-3\right)\left(x+3\right)\)
\(=x^2+2x+1-x^2+2x-1-3\left(x^2-9\right)\)
\(=4x-3x^2+27\)
6: \(\left(x-1\right)^3-x\left(x-2\right)^2+x-1\)
\(=x^3-3x^2+3x-1-x\left(x^2-4x+4\right)+x-1\)
\(=x^3-3x^2+4x-2-x^3+4x^2-4x\)
\(=x^2-2\)
7: \(\left(x+2\right)^3-x^2\left(x+6\right)-8\)
\(=x^3+6x^2+12x+8-x^3-6x^2-8\)
=12x
8: \(\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=\left(x^3+3x^2y+3xy^2+y^3\right)-\left(x^3-3x^2y+3xy^2-y^3\right)-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)
9: \(\left(x-1\right)^3-\left(x+1\right)^3+6\left(x-1\right)\left(x+1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6\left(x^2-1\right)\)
\(=-6x^2-2+6x^2-6=-8\)
10: \(4x\left(3x-5\right)-2\left(4x+1\right)-x-7\)
\(=12x^2-20x-8x-2-x-7\)
\(=12x^2-29x-9\)
11: \(\left(3x+1\right)^2-2\left(3x+1\right)\left(5x+5\right)+\left(5x+5\right)^2\)
\(=\left(5x+5-3x-1\right)^2\)
\(=\left(2x+4\right)^2=4x^2+16x+16\)
12: \(\left(2x+3\right)^2+\left(2x+3\right)\left(2x-6\right)+\left(x-3\right)^2\)
\(=\left(2x+3\right)^2+2\cdot\left(2x+3\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+3+x-3\right)^2=\left(3x\right)^2=9x^2\)
13: \(\left(x^2-2x+4\right)\left(x+2\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
\(=x^3+8-x^3-3x^2-3x-1+3\left(x^2-1\right)\)
\(=-3x^2-3x+7+3x^2-3=-3x+4\)
14: \(\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+4\left(x+1\right)^2\)
\(=\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+\left(2x+2\right)^2\)
\(=\left(x-2+2x+2\right)^2=\left(3x\right)^2=9x^2\)

Lời giải:
Áp dụng BĐT Cô-si:
$\frac{x^2+y^2}{4}+\frac{1}{x^2+y^2}\geq 2\sqrt{\frac{x^2+y^2}{4}.\frac{1}{x^2+y^2}}=1$
Áp dụng BĐT Bunhiacopxky:
$\frac{3(x^2+y^2)}{4}=\frac{3(1+1)(x^2+y^2)}{8}\geq \frac{3(x+y)^2}{8}=\frac{3.2^2}{8}=\frac{3}{2}$
$\Rightarrow B\geq 1+\frac{3}{2}=\frac{5}{2}$
Vậy $B_{\min}=\frac{5}{2}$
Giá trị này đạt tại $x=y=1$

\(3\left(\dfrac{1}{5}-x\right)=-\dfrac{9}{5}\)
⇔\(\left(\dfrac{1}{5}-x\right)=-\dfrac{9}{5}:3\)
⇔\(\left(\dfrac{1}{5}-x\right)=-\dfrac{9}{5}.\dfrac{1}{3}\)
⇔\(\left(\dfrac{1}{5}-x\right)=-\dfrac{3}{5}\)
⇔\(x=\dfrac{1}{5}-\left(-\dfrac{3}{5}\right)\)
⇔\(x=\dfrac{1}{5}+\dfrac{3}{5}\)
⇔\(x=\dfrac{4}{5}\)
Vậy \(x=\dfrac{4}{5}\)


12,6 × (y - 2) - y × 5,6 = 16,8
12,6 × y - 25,2 - y × 5,6 = 16,8
y × (12,6 - 5,6) = 16,8 + 25,2
y × 7 = 42
y = 42 : 7
y = 6

Số chữ số dùng để đánh số các số chẵn có 1 chữ số: 4 (chữ số)
Từ 10 đến 98 có số các số chẵn là:
(98 - 10) : 2 + 1 = 45 (số)
Số các chữ số dùng để đánh số các số chẵn từ 10 đến 98 là:
45 . 2 = 90 (chữ số)
Từ 100 đến 284 có số các số chẵn là:
(284 - 100) : 2 + 1 = 93 (số)
Số chữ số dùng để đánh số các số chẵn từ 100 đến 284 là:
93 . 3 = 279 (chữ số)
Số chữ số đã dùng để đánh số nhà chẵn:
279 + 90 + 4 = 373 (chữ số)
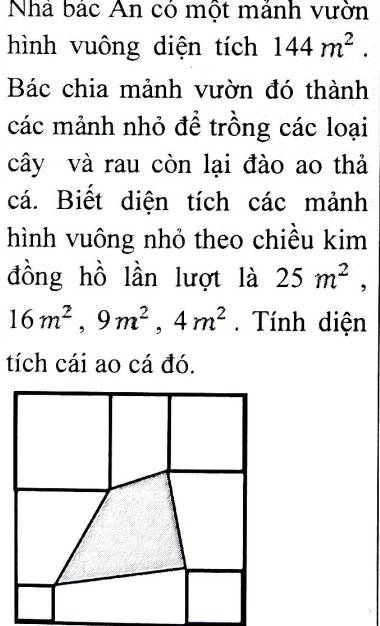
Ta đánh số các hình như hình minh họa khi đó ta có:
Vì 144 = 12 x 12
Vậy cạnh hình vuông mảnh đất là 12 m
25 = 5 x 5; 16 = 4 x 4 ; 9 = 3 x 3; 4 = 2 x 2
Vậy cạnh hình vuông của các mảnh đất nhỏ theo thứ tự chiều kim đồng hồ lần lượt là:
5m; 4m; 3m; 2m
Chiều cao của hình thang thứ nhất:
12 - 5 - 4 = 3 (m)
Chiều cao của hình thang thứ hai là:
12 - 4 - 3 = 5(m)
Chiều cao của hình thang thứ tư là:
12 - 3 - 2 = 7 (m)
Diện tích hình thang thứ nhất là:
(5 + 4) x 3 : 2 = 13,5 (m2)
Diện tích hình thang thứ hai là:
(4 + 3) x 5 : 2 = 17,5 (m2)
Diện tích hình thang thứ ba là:
(3 + 2) x 7: 2 = 17,5 (m2)
Diện tích hình thang thứ tư là:
(2 + 5) x 5 : 2 = 17,5 (m2)
Diện tích ao cá là:
144 - 13,5 - 17,5 - 17,5 - 17,5 = 78 (m2)
Đáp số: 78 m2
ko ai bt ah