a)

`2x+4=x-1`

`<=>2x-x=-4-1`

`<=>x=-5`

Vậy phương trình có tập nghiệm là : \(S=\left\{-5\right\}\)

b)

`2x(x-3)-5(x-3)=0`

`<=>(x-3)(2x-5)=0`

`=>x-3=0` hoặc `2x-5=0`

`<=>x=3` hoặc `x=5/2`

Vậy tập nghiệm phương trình là : \(S=\left\{3;\dfrac{5}{2}\right\}\)

c)

\(\dfrac{2x}{x+1}=\dfrac{x^2-x+8}{\left(x+1\right)\left(x-4\right)}\left(x\ne\left\{-1;4\right\}\right)\\ < =>\dfrac{2x\left(x-4\right)}{\left(x+1\right)\left(x-4\right)}=\dfrac{x^2-x+8}{\left(x+1\right)\left(x-4\right)}\\ =>2x\left(x-4\right)=x^2-x+8\\ < =>2x^2-8x=x^2-x+8\\ < =>2x^2-x^2-8x+x-8=0\\ < =>x^2-7x-8=0\\ < =>\left(x-8\right)\left(x+1\right)=0\\ =>\left[{}\begin{matrix}x=8\left(N\right)\\x=-1\left(L\right)\end{matrix}\right.\)

Vậy tập nghiệm phương trình là : \(S=\left\{8\right\}\)

`x^2-4x+y^2-6y+15=2`

`<=>x^2-4x+4+y^2-6y+9=0`

`<=>(x-2)^2+(y-3)^2=0`

 `=>x-2=0` và `y-3=0`

`<=>x=2` và `y=3`

Ta có: 

$\begin{array}{rl}& x^2-4x+y^2-6y+15=2\\ \iff & x^2-4x+4+y^2-6y+9=0\\ \iff & (x-2{)}^2+(y-3{)}^2=0\\ \iff & \{\begin{array}{l}{\left(x-2\right)}^2=0\\ {\left(y-3\right)}^2=0\end{array}\iff \{\begin{array}{l}x=2\\ y=3\end{array}\end{array}$

(vì $(x-2{)}^2\ge 0$ với mọi $x\in \mathbb{R}$, $(y-3{)}^2\ge 0$ với mọi $y\in \mathbb{R}$).

Vậy $x=2$, $y=3$. 

a) Vì tam giác ABC vuông tại A

Áp dụng định lý Pytago :

AB² + AC² = BC²

<=> 6² + 8² = BC²

<=> BC = 10

BD tia phân giác góc B nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}=\dfrac{3}{5}\)(1)

mà AD + DC = AC = 8 (2) 

Từ (1)(2) ta tìm được AD = 3 ; DC = 5

=> P = AD.DC = 3.5 = 15 

b) Mà \(BD\cap AH=\left\{I\right\}\)

\(\Rightarrow\dfrac{AI}{IH}=\dfrac{AB}{BH}\)(3)

Xét tam giác ABH và tam giác ABC có

\(\widehat{ABC}\) chung ; \(\widehat{AHB}=\widehat{BAC}=90^{\text{o}}\) 

nên \(\Delta CBA\sim\Delta ABH\)

\(\Rightarrow\dfrac{BH}{AB}=\dfrac{AB}{BC}\)

\(\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\)( kết hợp (1);(3))

c) Tương tự dễ thấy

\(\Delta BIH\sim\Delta BDA\) (g-g)

=> \(\widehat{BDA}=\widehat{BIH}\)

lại có \(\widehat{BIH}=\widehat{AID}\) (đối đỉnh)

nên \(\widehat{BDA}=\widehat{AID}\) => Tam giác AID cân tại A

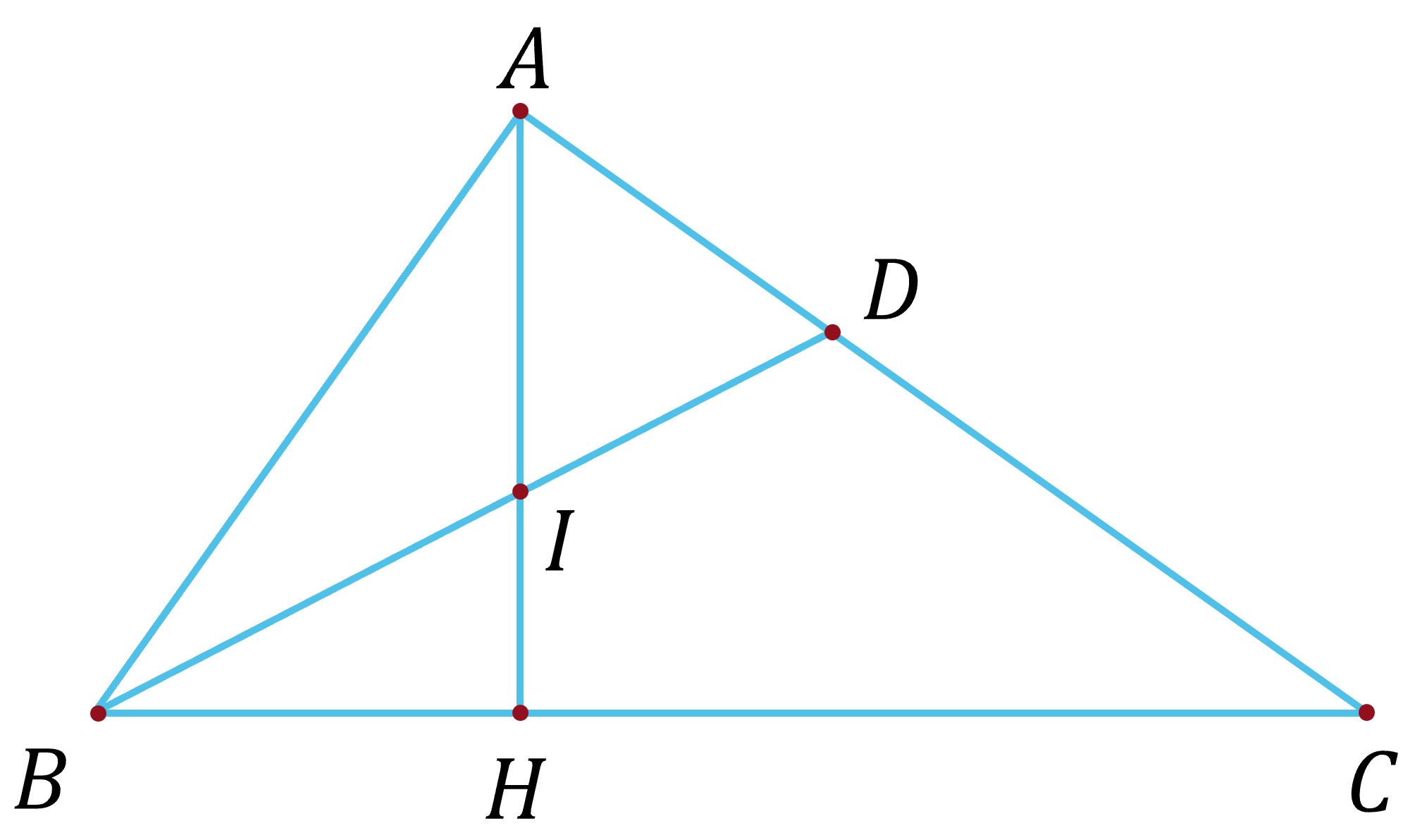
a) Xét tam giác $ABC$ vuông tại $A$: 

$B{C}^2=A{B}^2+A{C}^2$ (định lí Pythagoras)

$\iff B{C}^2=6^2+8^2=100\iff BC=10(cm)$. 

Xét tam giác $ABC$ phân giác $BD$ có: 

$\genfrac{}{}{0ex}{}{AB}{BC}=\genfrac{}{}{0ex}{}{AD}{DC}\iff \genfrac{}{}{0ex}{}{AB}{BC+AB}=\genfrac{}{}{0ex}{}{AD}{DC+AD}$ 

$\genfrac{}{}{0ex}{}{AD}{AC}=\genfrac{}{}{0ex}{}{AB}{BC+AB}\iff AD=3(cm)$

suy ra $DC=5(cm)$.

b) Xét tam giác $ABH$ phân giác $BI$ có: $\genfrac{}{}{0ex}{}{IH}{IA}=\genfrac{}{}{0ex}{}{HB}{AB}$.

Xét $△HBA$ và $△ABC$ có: 

$\widehat{HBA}=\widehat{ABC}$ (góc chung)

$\widehat{BHA}=\widehat{BAC}(=90^{\circ })$

suy ra $△HBA\sim △ABC$ (g.g).

Suy ra $\genfrac{}{}{0ex}{}{HB}{AB}=\genfrac{}{}{0ex}{}{BA}{BC}$ 

$\Rightarrow \genfrac{}{}{0ex}{}{BA}{BC}=\genfrac{}{}{0ex}{}{IH}{IA}$. 

Mà ta lại có $\genfrac{}{}{0ex}{}{AB}{BC}=\genfrac{}{}{0ex}{}{AD}{DC}$ nên $\genfrac{}{}{0ex}{}{IH}{IA}=\genfrac{}{}{0ex}{}{AD}{DC}$. 

c) Ta có $△ABD\sim △HBI$ (g.g) 

suy ra $\genfrac{}{}{0ex}{}{AB}{HB}=\genfrac{}{}{0ex}{}{BD}{BI}\Rightarrow AB.BI=BD.HB$.

$\widehat{BDA}=\widehat{BIH}$ (hai góc tương ứng) 

mà $\widehat{BIH}=\widehat{AID}$ (hai góc đối đỉnh)

suy ra $\widehat{BDA}=\widehat{AID}$ 

do đó tam giác $AID$ cân tại $A$.

Cái này anh thấy có vẻ chưa đúng đề lắm em ạ

Vì 440 không chia hết cho 3 nên sao bằng được

`1/9(x-3)^2-1/25(x+5)^2=0`

`<=>(1/3x-1)^2-(1/5x+1)^2=0`

`<=>(1/3x-1-1/5x-1)(1/3x-1+1/5x+1)=0`

`<=>(2/15x-2). 8/15x=0`

`<=>2/15x-2=0` hoặc `8/15x=0`

`<=>x=15`         hoặc `x=0`

Vậy `S=`{`15;0`}

Gọi số đó là \(\overline{ab}\)

Vì đó là số lẻ chia hết cho `5` nên `b=5`

  \(=>\overline{a5}\)

Vì hiện của số đó và chữ số hàng chục của nó bằng `86` nên ta có:

  \(overline{a5}-a=86\)

\(<=>10a+5-a=86\)

`<=>a=9`

Vậy số cần tìm là `95`

Sửa lỗi chỗ `overlinea5` thành \(\overline{a5}\)

a)

\(\dfrac{x-3}{5}+\dfrac{1-2x}{3}=6\\ < =>3x-9+5-10x=90\)

\(< =>3x-10x=90+9-5\\ < =>-7x=94\\ < =>x=-\dfrac{94}{7}\)

b)

\(\left(2x-3\right)\left(x^2+1\right)=0\\ < =>\left[{}\begin{matrix}2x-3=0\\x^2+1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{3}{2}\\x^2=-1\left(voli\right)\end{matrix}\right.\\ < =>x=\dfrac{3}{2}\)

c)

\(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\left(x\ne-1;x\ne2\right)\)

suy ra: \(2\left(x-2\right)-x-1=3x-11\)

\(< =>2x-4-x-1-3x+11=0\)

\(< =>2x-x-3x=4+1-11\\ < =>-2x=-6\\ < =>x=3\left(tm\right)\)

a) \(\dfrac{x-3}{5}+\dfrac{1-2x}{3}=6\)

\(\Leftrightarrow3\left(x-3\right)+5\left(1-2x\right)=90\)

\(\Leftrightarrow-4-7x=90\)

\(\Leftrightarrow x=-\dfrac{94}{7}\)

b) \(\left(2x-3\right)\left(x^2+1\right)=0\)

\(\Leftrightarrow2x-3=0\) (Vì \(x^2+1>0\))

\(\Leftrightarrow x=\dfrac{3}{2}\)

c) \(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\left(Đk:x\ne-1;x\ne2\right)\)

\(\Leftrightarrow2\left(x-2\right)-\left(x+1\right)=3x-11\)

\(\Leftrightarrow x-5=3x-11\)

\(\Leftrightarrow x=3\)

a) ĐKXĐ : \(\left\{{}\begin{matrix}3x-2\ne0\\3x+2\ne0\\4-9x^2\ne0\end{matrix}\right.\Leftrightarrow x\ne\pm\dfrac{2}{3}\)

\(C=\dfrac{1}{3x-2}-\dfrac{4}{3x+2}-\dfrac{3x-6}{4-9x^2}\)

\(=\dfrac{3x+2}{\left(3x-2\right)\left(3x+2\right)}-\dfrac{4.\left(3x-2\right)}{\left(3x-2\right)\left(3x+2\right)}+\dfrac{3x-6}{9x^2-4}\)

\(=\dfrac{3x+2-4.\left(3x-2\right)+3x-6}{\left(3x-2\right).\left(3x+2\right)}=\dfrac{-6x+4}{\left(3x-2\right).\left(3x+2\right)}\)

\(=\dfrac{-2}{3x+2}\)

b) Với \(x\inℤ\) 

Ta có  : \(C\inℤ\Leftrightarrow-2⋮3x+2\)

\(\Leftrightarrow3x+2\inƯ\left(-2\right)\)

\(\Leftrightarrow3x+2\in\left\{1;2;-1;-2\right\}\)

Lập bảng 

Vậy \(x\in\left\{0;-1\right\}\)

Ta có  : 

Lập bảng 

3x + 2	1	2	-2	-1
x		0(tm)		-1(tm)

Vậy