Bài 8 (trang 120 SGK Hình học 11): Cho tứ diện ABCD cạnh a. Tính khoảng cách giữa hai cạnh đối diện của tứ diện đều đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






Cách 1:
d:2x−y+1=0d:2x−y+1=0
Chọn 2 điểm bất kỳ thuộc đường thẳng dd là:
A(0;1)A(0;1) và B(1;3)B(1;3)
Q(O;−90o)A(0;1)=A′(1;0)Q(O;−90o)A(0;1)=A′(1;0)
Q(O;−90o)B(1;3)=B′(3;−1)Q(O;−90o)B(1;3)=B′(3;−1)
Ảnh d′d′ của đường thẳng dd qua phép Q(O;−90o)Q(O;−90o)
là đường thẳng đi qua 2 điểm A′(1;0)A′(1;0) và B′(3;−1)B′(3;−1)
Phương trình đường thẳng d′d′ là:
x−13−1=y−0−1−0x−13−1=y−0−1−0
⇔−(x−1)=2y⇔−(x−1)=2y
⇔x+2y−1=0⇔x+2y−1=0
Cách 2:
Ảnh d′d′ của đường thẳng d:2x−y+1=0d:2x−y+1=0 qua phép Q(O;−90o)Q(O;−90o) là đường thẳng vuông góc với đường thẳng dd
nên phương trình d′d′ có dạng: x+2y+z=0x+2y+z=0
trên đường thẳng dd chọn 1 điểm bất kỳ là A(0;1)A(0;1) như vậy
Q(O;−90o)A(0;1)=A′(1;0)Q(O;−90o)A(0;1)=A′(1;0) thuộc đường thẳng d′d′ nên tọa độ của A′A′ thỏa mãn phương trình đường thẳng d′d′, ta có:
1+2.0+z=0⇔z=−11+2.0+z=0⇔z=−1
Vậy phương trình đường thẳng d′:x+2y−1=0d′:x+2y−1=0


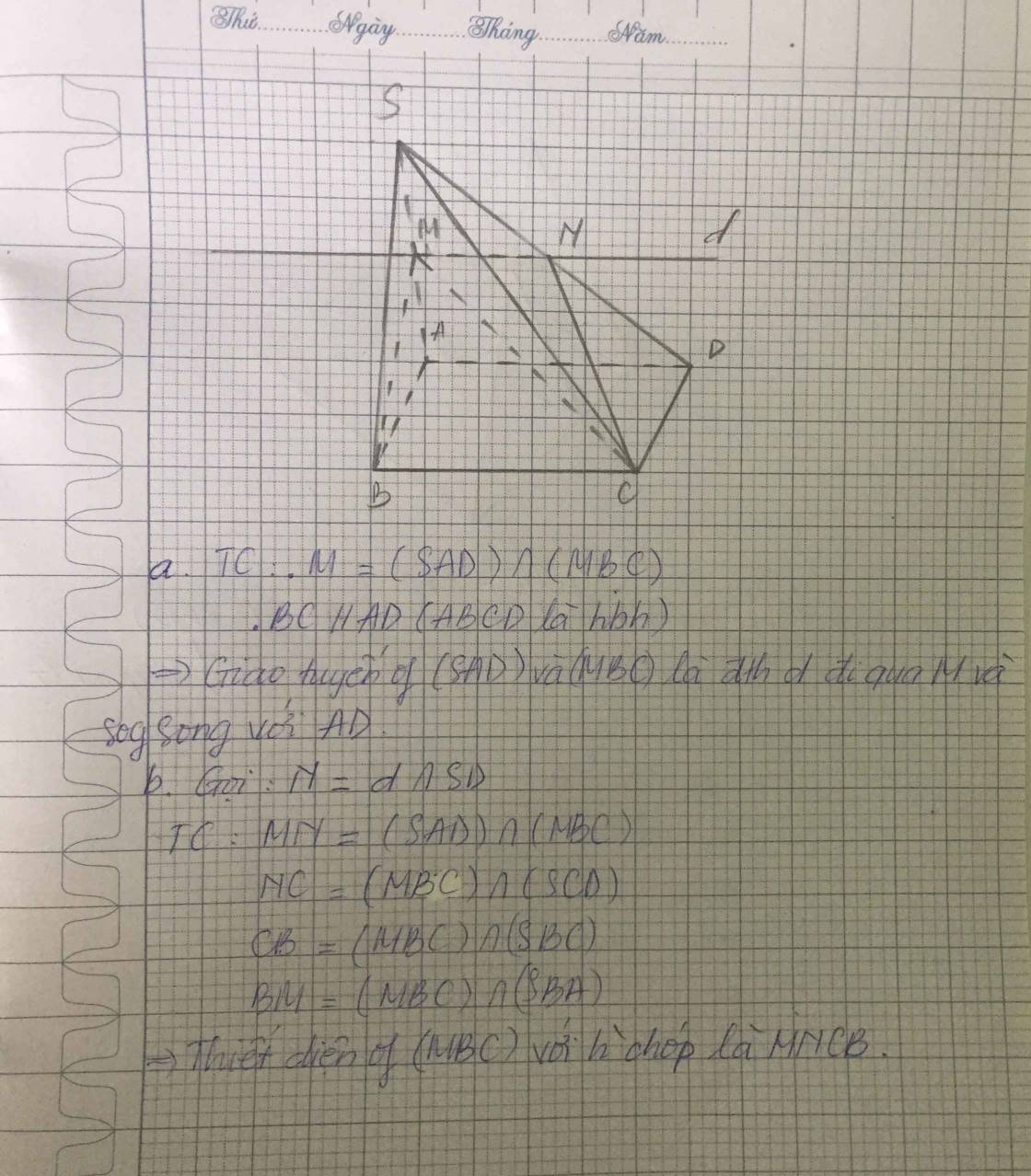
Hai tam giác CBA và DBA là hai tam giác đều cạnh a
=> ∆ CBA = ∆ DBA ( c.c.c)
=> CM = DM ( 2 đường trung tuyến tương ứng)
=> Tam giác CMD cân tại M.
Lại có: MN là đường trung tuyến nên đồng thời là đường cao: MN ⊥ CD
* Chứng minh tương tự, ta có: MN ⊥ AB
Do đó, MN là đoạn vuông góc chung của AB và CD.
* Tam giác BCD là tam giác đều cạnh a nên
\(BN=\sqrt{BC^2-CN^2}=\frac{a\sqrt{3}}{2}\)
Bài này học rồi mà bà