Cho \(B=2\left(4x^5+4x^4-5x^3+2x-2\right)^{2021}+2022\) Tính giá trị của B tại \(x=\dfrac{-1-\sqrt{5}}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{16+6\sqrt{7}}=\sqrt{9+2.3.\sqrt{7}+7}=\sqrt{\left(3+\sqrt{7}\right)^2}=\left|3+\sqrt{7}\right|=3+\sqrt{7}\)
\(\sqrt{16+6\sqrt{7}}=\sqrt{9+2.3\sqrt{7}+7}=\sqrt{3^2+2.3\sqrt{7}+\left(\sqrt{7}\right)^2}\)\(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)




Nguyên nhân thắng lợi:
- Sự lãnh đạo sáng suốt của Đảng, và Chủ tịch Hồ Chí Minh, với đường lối chính trị, quân sự độc lập, tự chủ đúng đắn, sáng tạo, phương pháp đấu tranh linh hoạt.
- Hậu phương miền Bắc không ngừng lớn mạnh, đáp ứng kịp thời các yêu cầu của cuộc chiến đấu ở hai miền.
- Có sự phối hợp chiến đấu, đoàn kết giúp đỡ nhau của ba dân tộc ở Đông Dương; sự đồng tình ủng hộ, giúp đỡ to lớn của các nước xã hội chủ nghĩa khác; nhân dân Mĩ và nhân dân thế giới phản đối cuộc đấu tranh xâm lược Việt Nam của Mĩ.
Nguyên nhân quan trọng nhất là sự phối hợp chiến đấu, đoàn kết giúp đỡ nhau và có những người lãnh đạo sáng suốt . Vì đoàn kết nhau chúng ta sẽ có nguồn sức mạnh to lớn và cần các người lãnh đạo sáng suốt, sáng tạo sẽ giúp chúng ta thắng lợi to lớn
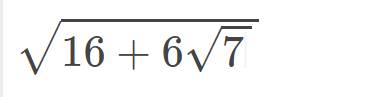 mọi người giúp mình câu này với ạ
mọi người giúp mình câu này với ạ