
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(x^2+y^2+z^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}=6 \)
\(\Leftrightarrow x^2+y^2+z^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}-6=0\\ \Leftrightarrow\left(x^2+\dfrac{1}{x^2}-2\right)+\left(y^2+\dfrac{1}{y^2}-2\right)+\left(z^2+\dfrac{1}{z^2}-2\right)=0\\ \Leftrightarrow\left(x^2-2\cdot x^2\cdot\dfrac{1}{x^2}+\dfrac{1}{x^2}\right)+\left(y^2-2\cdot y^2\cdot\dfrac{1}{y^2}+\dfrac{1}{y^2}\right)+\left(z^2-2\cdot z^2\cdot\dfrac{1}{z^2}+\dfrac{1}{z^2}\right)=0\\ \Leftrightarrow\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2+\left(z-\dfrac{1}{z}\right)^2=0\)
Mà: \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{x}\right)^2\ge0\forall x\\\left(y-\dfrac{1}{y}\right)^2\ge0\forall y\\\left(z-\dfrac{1}{z}\right)^2\ge0\forall z\end{matrix}\right.=>\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2+\left(z-\dfrac{1}{z}\right)^2\ge0\forall x,y,z\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}x=\dfrac{1}{x}\\y=\dfrac{1}{y}\\z=\dfrac{1}{z}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=1\\y^2=1\\z^2=1\end{matrix}\right.\)
\(P=x^{2024}+y^{2024}+z^{2024}\\=\left(x^2\right)^{1012}+\left(y^2\right)^{1012}+\left(z^2\right)^{1012}\\ =1^{1012}+1^{1012}+1^{1012}=3\)

Trên nửa mặt phẳng có bờ chứa tia Ox, có 2 tia oz và oy mà góc xOz < góc xOy ( 30độ < 110 độ) nên tia Oz nằm giữa 2 tia Ox và Oy
Ta có : xOz + zOy = xOy
30 + zOy = 110
zoy = 110 - 30 = 80
ot là tia phân giác của zOy nen zot = toy = 80 : 2 = 40
xot = zot + xoz = 40 + 30 = 70
vậy
yOz = 80 độ
zOt = 40 độ
xOt = 70 độ

a: \(8^{24}=\left(2^3\right)^{24}=2^{72};16^{20}=\left(2^4\right)^{20}=2^{80}\)
mà 72<80
nên \(8^{24}< 16^{20}\)
b: \(\left(-\dfrac{1}{25}\right)^{37}=-\left(\dfrac{1}{5}\right)^{74}=-\dfrac{1}{5^{74}};\left(-\dfrac{1}{125}\right)^{23}=-\dfrac{1}{\left(5^3\right)^{23}}=-\dfrac{1}{5^{69}}\)
\(5^{74}>5^{69}\)
=>\(\dfrac{1}{5^{74}}< \dfrac{1}{5^{69}}\)
=>\(-\dfrac{1}{5^{74}}>-\dfrac{1}{5^{69}}\)
=>\(\left(-\dfrac{1}{25}\right)^{37}>\left(-\dfrac{1}{125}\right)^{23}\)
c: \(A=\dfrac{3}{7^3}+\dfrac{5}{7^4}=\dfrac{3\cdot7+5}{7^4}=\dfrac{26}{7^4}\)
\(B=\dfrac{5}{7^3}+\dfrac{3}{7^4}=\dfrac{5\cdot7+3}{7^4}=\dfrac{38}{7^4}\)
mà 26<38
nên A<B
d: \(10A=\dfrac{10^8+10}{10^8+1}=1+\dfrac{9}{10^8+1}\)
\(10B=\dfrac{10^9+10}{10^9+1}=1+\dfrac{9}{10^9+1}\)
Ta có: \(10^8+1< 10^9+1\)
=>\(\dfrac{9}{10^8+1}>\dfrac{9}{10^9+1}\)
=>\(\dfrac{9}{10^8+1}+1>\dfrac{9}{10^9+1}+1\)
=>10A>10B
=>A>B

a: \(\left(\dfrac{1}{16}\right)^x=\left(\dfrac{1}{2}\right)^{10}\)
=>\(\left(\dfrac{1}{2}\right)^{4x}=\left(\dfrac{1}{2}\right)^{10}\)
=>4x=10
=>x=2,5
b: \(\left(-\dfrac{8}{13}\right)^x=\dfrac{64}{169}\)
=>\(\left(-\dfrac{8}{13}\right)^x=\left(-\dfrac{8}{13}\right)^2\)
=>x=2
c: \(\left(\dfrac{1}{64}\right)^x=\left(-\dfrac{1}{8}\right)^{14}\)
=>\(\left(\dfrac{1}{64}\right)^x=\left(\dfrac{1}{64}\right)^7\)
=>x=7
d: \(\dfrac{27-x}{23}+\dfrac{28-x}{24}=\dfrac{29-x}{25}+\dfrac{30-x}{26}\)
=>\(\left(\dfrac{27-x}{23}-1\right)+\left(\dfrac{28-x}{24}-1\right)=\left(\dfrac{29-x}{25}-1\right)+\left(\dfrac{30-x}{26}-1\right)\)
=>\(\dfrac{4-x}{23}+\dfrac{4-x}{24}=\dfrac{4-x}{25}+\dfrac{4-x}{26}\)
=>\(\left(4-x\right)\left(\dfrac{1}{23}+\dfrac{1}{24}-\dfrac{1}{25}-\dfrac{1}{26}\right)=0\)
=>4-x=0
=>x=4

a: \(64^x:16^x=256\)
=>\(\left(\dfrac{64}{16}\right)^x=256\)
=>\(4^x=256=4^4\)
=>x=4
b: \(-\dfrac{2401}{7^x}=-7\)
=>\(\dfrac{2401}{7^x}=7\)
=>\(7^x=\dfrac{2401}{7}=343=7^3\)
=>x=3
c: \(\dfrac{625}{\left(-5\right)^x}=25\)
=>\(\left(-5\right)^x=\dfrac{625}{25}=25=\left(-5\right)^2\)
=>x=2
a) $64^x:16^x=256$
$\Rightarrow (4^3)^x:(4^2)^x=256$
$\Rightarrow (4^3:4^2)^x=256$
$\Rightarrow 4^x=4^4$
$\Rightarrow x=4$ (tmdk)
b) $\frac{-2401}{7^x}=-7$
$\Rightarrow 7^x=-2401:(-7)$
$\Rightarrow 7^x=343$
$\Rightarrow 7^x=7^3$
$\Rightarrow x=3$ (tmdk)
c) $\frac{625}{(-5)^x}=25$
$\Rightarrow (-5)^x=625:25$
$\Rightarrow (-5)^x=25$
$\Rightarrow (-5)^x=(-5)^2$
$\Rightarrow x=2$ (tmdk)

a: \(\left(\dfrac{2}{3}\right)^6\cdot\left(\dfrac{8}{27}\right)^2=\left(\dfrac{2}{3}\right)^6\cdot\left(\dfrac{2}{3}\right)^6=\left(\dfrac{2}{3}\right)^{12}\)
b: \(\left(\dfrac{3}{5}\right)^2\cdot\left(-\dfrac{9}{25}\right)^2=\left(\dfrac{3}{5}\right)^2\cdot\left(\dfrac{9}{25}\right)^2\)
\(=\left(\dfrac{3}{5}\right)^2\cdot\left(\dfrac{3}{5}\right)^4=\left(\dfrac{3}{5}\right)^6\)
c: \(\left(-\dfrac{5}{2}\right)^3:\left(-\dfrac{8}{125}\right)^3\)
\(=\left(-\dfrac{5}{2}:\dfrac{-8}{125}\right)^3=\left(\dfrac{5}{2}\cdot\dfrac{125}{8}\right)^3=\left(\dfrac{625}{16}\right)^3\)
\(=\left(\dfrac{5}{2}\right)^{12}\)

a: \(\left(\dfrac{2}{3}\right)^5=\dfrac{2^5}{3^5}=\dfrac{32}{243}\)
\(\left(-\dfrac{2}{3}\right)^5=\dfrac{\left(-2\right)^5}{3^5}=\dfrac{-32}{243}\)
\(\left(-1\dfrac{3}{4}\right)^2=\left(-\dfrac{7}{4}\right)^2=\left(\dfrac{7}{4}\right)^2=\dfrac{49}{16}\)
\(\left(-0,1\right)^4=\left(0,1\right)^4=\left(\dfrac{1}{10}\right)^4=\dfrac{1}{10^4}=\dfrac{1}{10000}\)
b: \(\dfrac{90^3}{15^3}=\left(\dfrac{90}{15}\right)^3=6^3=216\)
\(\dfrac{790^4}{79^4}=\left(\dfrac{790}{79}\right)^4=10^4=10000\)
\(\dfrac{3^2}{15^2}=\left(\dfrac{3}{15}\right)^2=\left(\dfrac{1}{5}\right)^2=\dfrac{1}{25}\)
\(\dfrac{\left(-\dfrac{1}{2}\right)^n}{\left(-\dfrac{1}{2}\right)^{n-1}}=\left(-\dfrac{1}{2}\right)^{n-n+1}=\left(-\dfrac{1}{2}\right)^1=-\dfrac{1}{2}\)

Câu 1:
a: \(-\dfrac{9}{51}\cdot\dfrac{17}{6}=\dfrac{-9}{6}\cdot\dfrac{17}{51}=\dfrac{-3}{2}\cdot\dfrac{1}{3}=-\dfrac{1}{2}\)
b: \(-\dfrac{25}{32}\cdot\left(-0,2\right)=\dfrac{25}{32}\cdot0,2=\dfrac{5}{32}\)
c: \(-15,2\cdot3,5=-53,2\)
d: \(-\dfrac{8}{15}\cdot1\dfrac{1}{4}=-\dfrac{8}{15}\cdot\dfrac{5}{4}=-\dfrac{8}{4}\cdot\dfrac{5}{15}=-\dfrac{2}{3}\)
e: \(1\dfrac{2}{5}\cdot\dfrac{-3}{14}=\dfrac{7}{5}\cdot\dfrac{-3}{14}=-\dfrac{21}{70}=-\dfrac{3}{10}\)
f: \(1\dfrac{1}{17}\cdot1\dfrac{1}{36}=\dfrac{18}{17}\cdot\dfrac{37}{36}=\dfrac{18}{36}\cdot\dfrac{37}{17}=\dfrac{37}{17}\cdot\dfrac{1}{2}=\dfrac{37}{34}\)
Câu 2:
a: \(-\dfrac{5}{2}:\dfrac{5}{8}=-\dfrac{5}{2}\cdot\dfrac{8}{5}=-\dfrac{8}{2}=-4\)
b: \(4\dfrac{1}{5}:\left(-2\dfrac{4}{5}\right)=\dfrac{-21}{5}:\dfrac{14}{5}=-\dfrac{21}{5}\cdot\dfrac{5}{14}=-\dfrac{21}{14}=-\dfrac{3}{2}\)
c: \(7:\left(-3,5\right)=-\dfrac{7}{3,5}=-2\)
d: \(-1\dfrac{4}{5}:\dfrac{-3}{4}=\dfrac{-9}{5}\cdot\dfrac{-4}{3}=\dfrac{-9}{3}\cdot\dfrac{-4}{5}=\dfrac{3\cdot4}{5}=\dfrac{12}{5}\)
e: \(4,2:\dfrac{-15}{12}=4,2:\dfrac{-5}{4}=4,2\cdot\dfrac{-4}{5}=-\dfrac{16.8}{5}=-3,36\)
f: \(6\dfrac{9}{11}:\left(-3\right)=-\dfrac{75}{11}\cdot\dfrac{1}{3}=-\dfrac{25}{11}\)

Bài 6:
\(a)P=\dfrac{2}{1\cdot5}+\dfrac{2}{5\cdot9}+...+\dfrac{2}{33\cdot37}+\dfrac{2}{37\cdot41}\\ =\dfrac{1}{2}\cdot\left(\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{33\cdot37}+\dfrac{4}{37\cdot41}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{33}-\dfrac{1}{37}+\dfrac{1}{37}-\dfrac{1}{41}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{41}\right)\\ =\dfrac{1}{2}\cdot\dfrac{40}{41}\\ =\dfrac{20}{41}\\ b)Q=\dfrac{6}{2\cdot9}+\dfrac{6}{9\cdot16}+...+\dfrac{6}{114\cdot121}\\ =\dfrac{6}{7}\cdot\left(\dfrac{7}{2\cdot9}+\dfrac{7}{9\cdot16}+...+\dfrac{7}{114\cdot121}\right)\\ =\dfrac{6}{7}\cdot\left(\dfrac{1}{2}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{114}-\dfrac{1}{121}\right)\\ =\dfrac{6}{7}\cdot\left(\dfrac{1}{2}-\dfrac{1}{121}\right)\\ =\dfrac{6}{7}\cdot\dfrac{119}{242}\\ =\dfrac{51}{121}\)
Bài 5:
a: Để A>0 thì \(\dfrac{2a-1}{-5}>0\)
=>2a-1<0
=>\(a< \dfrac{1}{2}\)
b: Để A<0 thì \(\dfrac{2a-1}{-5}< 0\)
=>2a-1>0
=>2a>1
=>\(a>\dfrac{1}{2}\)
c: Để A=0 thì \(\dfrac{2a-1}{-5}=0\)
=>2a-1=0
=>2a=1
=>\(a=\dfrac{1}{2}\)
Bài 6:
a: \(P=\dfrac{2}{1\cdot5}+\dfrac{2}{5\cdot9}+...+\dfrac{2}{37\cdot41}\)
\(=\dfrac{2}{4}\cdot\left(\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{37\cdot41}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{37}-\dfrac{1}{41}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{41}\right)=\dfrac{1}{2}\cdot\dfrac{40}{41}=\dfrac{20}{41}\)
b: \(Q=\dfrac{6}{2\cdot9}+\dfrac{6}{9\cdot16}+...+\dfrac{6}{114\cdot121}\)
\(=\dfrac{6}{7}\left(\dfrac{7}{2\cdot9}+\dfrac{7}{9\cdot16}+...+\dfrac{7}{114\cdot121}\right)\)
\(=\dfrac{6}{7}\left(\dfrac{1}{2}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{114}-\dfrac{1}{121}\right)\)
\(=\dfrac{6}{7}\left(\dfrac{1}{2}-\dfrac{1}{121}\right)=\dfrac{6}{7}\cdot\dfrac{119}{242}=\dfrac{51}{121}\)

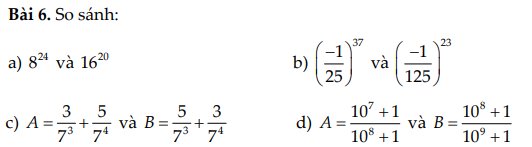
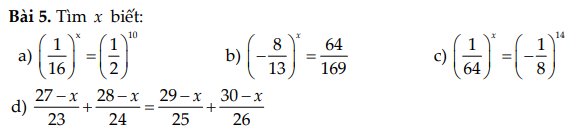
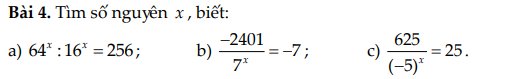
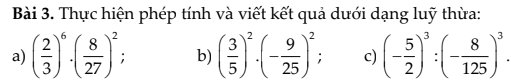
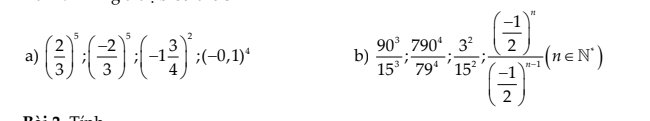


a) OA//IC => \(\widehat{CKB}=\widehat{AOK}=50^o\) (đồng vị)
OB//DE => \(\widehat{CID}=\widehat{CKB}=50^o\) (đồng vị)
b) Mà: \(\widehat{CIE}+\widehat{CID}=180^o\) (kề bù)
=> \(\widehat{CIE}=180^o-\widehat{CID}\)
=> \(\widehat{CIE}=180^o-50^o=130^o\)