Viết 3 số hữu tỉ có mẫu khác nhau lớn hơn -1 3 nhưng nhỏ hơn 4 5 ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = \(\dfrac{1}{\left|x+1\right|+\left|x-2022\right|}\)
Đặt B = \(\left|x+1\right|+\left|x-2022\right|\)
\(\left|x-2022\right|\) = \(\left|2022-x\right|\) ⇒ B = \(\left|x+1\right|+\left|2022-x\right|\)
B =\(\left|x+1\right|+\left|2022-x\right|\) ≥ \(\left|x+1+2022-x\right|\) = 2023
B(min) = 2023 ⇔ (\(x+1\))(2022-\(x\)) \(\ge\) 0
Lập bảng ta có:
| \(x\) | -1 2022 |
| \(x+1\) | - 0 + | + |
| \(2022-x\) | + | + 0 - |
| (\(x+1\))(\(2022-x\)) | - 0 + 0 - |
Theo bảng trên ta có: B(min) = 2023 ⇔ -1 ≤ \(x\) ≤ 2022
A = \(\dfrac{1}{\left|x+1\right|+\left|x-2022\right|}\)
Vì A dương nên A(max) ⇔ B(min) ⇔ B = 2023
A(max) = \(\dfrac{1}{2023}\) ⇔ -1 ≤ \(x\) ≤ 2022

X = {5; 7; 9; 11; 13;...;83}
Xét dãy số: 5; 7; 9;11; 13;...; 83
Dãy số trên là dãy số cách đều có khoảng cách là: 7 - 5 = 2
Phần tử thứ 11 của tập hợp X chính là số hạng thứ 11 của dãy số trên
Áp dụng công thức tính số thứ n của dãy số cách đều:
Stn = số đầu + khoảng cách \(\times\)(n-1)
Số thứ 11 của dãy số trên là: 5 + 2 \(\times\) ( 11 - 1) = 25
Kết luận:
Phần tử đứng thứ 11 tính từ trái qua phải của tập hợp X khi các phần tử của tập hợp X được sắp xếp theo thứ tự từ bé đến lớn là: 25

a) \(A=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2009.2010}\)
\(A=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2009}-\dfrac{1}{2010}\)
\(A=\dfrac{1}{1}-\dfrac{1}{2010}\)
\(A=\dfrac{2009}{2010}\)
b) \(B=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{2009.2011}\)
\(B=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2009}-\dfrac{1}{2011}\)
\(B=1-\dfrac{1}{2011}\)
\(B=\dfrac{2010}{2011}\)
b) B= \(\dfrac{2}{1.3}\)+ \(\dfrac{2}{3.5}\)+ ... + \(\dfrac{2}{2010.2012}\)
B= 1 - \(\dfrac{1}{3}\)+ \(\dfrac{1}{3}\) - \(\dfrac{1}{5}\)+...+ \(\dfrac{1}{2010}\) - \(\dfrac{1}{2012}\)
B= 1 - \(\dfrac{1}{2012}\)
B= \(\dfrac{2011}{2012}\)

Ta thấy ngay 1 quy luật là nếu số lẻ có dạng \(4k+1\) (số thứ tự của nó là lẻ) thì mang dấu dương còn nếu có dạng \(4k+3\) (số thứ tự của nó là chẵn) thì mang dấu âm. Trước hết ta tìm công thức tính giá trị tuyệt đối của số hạng thứ \(k\) của dãy, kí hiệu là \(u_k\), dễ thấy\(u_k=1+\left(k-1\right).2=2k-1\).
Bây giờ ta xét đến dấu của số hạng thứ \(k\). Như phân tích ở trên, nếu \(k\) lẻ thì \(u_k< 0\) còn nếu \(k\) lẻ thì \(u_k>0\). Do đó \(u_k=\left(-1\right)^{k+1}\left(2k-1\right)\)
Cái chỗ trị tuyệt đối mình kí hiệu là \(\left|u_k\right|\) đấy, mình quên.

Có a:b:c=2:4:5
\(\Rightarrow\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}\) \(=\dfrac{a+b-c}{2+4-5}=3\)
\(\dfrac{a}{2}=3\) \(\Rightarrow a=6\)
\(\dfrac{b}{4}=3\) \(\Rightarrow b=12\)
\(\dfrac{c}{5}=3\) \(\Rightarrow c=15\)
Ta có : \(\dfrac{a}{2}\) = \(\dfrac{b}{4}\) = \(\dfrac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau: ta có:
\(\dfrac{a}{2}\) = \(\dfrac{b}{4}\) = \(\dfrac{c}{5}\) = \(\dfrac{a+b-c}{2+4-5}\) = \(\dfrac{3}{1}\) = 3
\(a\) = 3 \(\times\) 2 = 6
\(b\) = 3 \(\times\) 4 = 12
\(c\) = 3 \(\times\) 5 = 15
Kết luận: \(a\) = 6; \(b\) = 12; \(c\) = 15

\(3^{n+2}+3^{n+1}-3^n=891\)
\(3^n\times3^2+3^n\times3-3^n=891\)
\(3^n\times\left(9+3-1\right)=891\)
\(3^n\times11=891\)
\(3^n=891\div11\)
\(3^n=81\)
\(3^n=3^4\)
\(n=4\)

Số chân chó là:
\(128\times4=512\left(chan\right)\)
Số chân mèo:
\(128\times4=512\left(chan\right)\)
Tổng chân chó và chân mèo:
\(512+512=1024\left(chan\right)\)
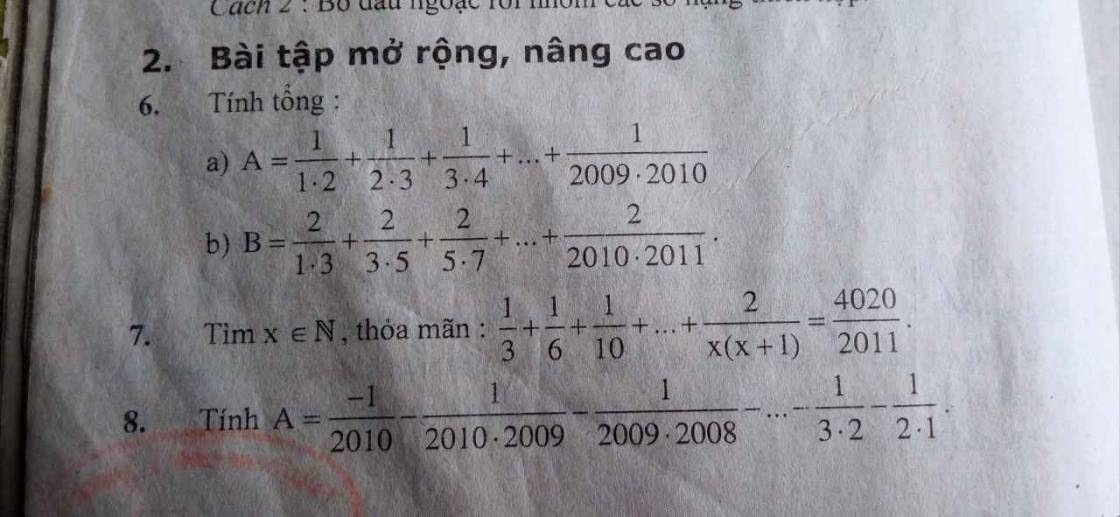
\(\dfrac{-1}{4};\dfrac{1}{2};\dfrac{6}{10}\)