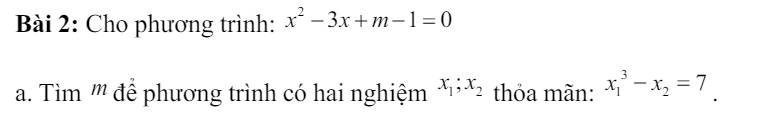Mít là loại trái cây rất giàu các chất dinh dưỡng quan trọng như vitamin A, vitamin C, canxi, kali,
sắt, thiamin, riboflavin, niacin, magneisum và nhiều chất dinh dưỡng khác. Vì vậy, mà chúng rất có lợi cho sức
khỏe con người. Mít tươi có 74% là nước. Trung bình 1 kg mít trái sẽ thu được 35% thịt múi mít. Mít tươi có 74% là nước, khi mang sấy khô thì tỉ lệ nước còn 20%. Công ty X thu mua 10 tấn mít trái với giá 15.000 đồng ký. Sau khi sấy khô thì công ty phải bán với giá bao nhiêu để có lãi 25% so với giá vốn. (kết quả làm tròn đến hàng nghìn).13:38/-strong/-heart:>:o:-((:-hĐã gửiXem trước khi gửiThả Files vào đây để xem lại trước khi gửi