Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tổ 1 làm được: \(180\times\dfrac{1}{3}=60\left(bông\right)\)
Tổ 2 làm được: \(180\times\dfrac{2}{3+2}=180\times\dfrac{2}{5}=72\left(bông\right)\)
Tổ 3 làm được:
180-60-72=48(bông)
gọi x là số bông tổ 1 làm; y là số bông tổ 2 làm; z là số bông tổ 3 làm
theo đề ta có: x + y + z = 180
số bông tổ 1 là: \(x=\dfrac{1}{3}\cdot80=60\)
số bông tổ 2 là: \(y=\dfrac{2}{3}\cdot\left(x+z\right)\)
\(y=\dfrac{2}{3}\cdot\left(60+z\right)=40+\dfrac{2}{3}z\)
\(60+\left(40+\dfrac{2}{3}\right)+z=180\\ 100+\dfrac{5}{3}z=180\\ \dfrac{5}{3}z=80\\ z=48\\ -------\\ y=40+\dfrac{2}{3}\cdot48=40+32=72\)
vậy số bông tổ 1 đạt là: 60
số bông tổ 2 là: 72
số bông tổ 3 là 48

Giả sử bạn có 1 đề xi mét khối nước. Khi nước đóng băng, thể tích tăng lên khoảng 9%. Do đó, thể tích tảng băng sẽ là:
Thể tıˊch tảng ba˘ng=Thể tıˊch nước ban đaˆˋu+Thể tıˊch ta˘ng theˆm\text{Thể tích tảng băng} = \text{Thể tích nước ban đầu} + \text{Thể tích tăng thêm}
Thể tích tăng thêm là 9% của 1 đề xi mét khối nước:
Thể tıˊch ta˘ng theˆm=1 dm3×0.09=0.09 dm3\text{Thể tích tăng thêm} = 1 \, \text{dm}^3 \times 0.09 = 0.09 \, \text{dm}^3
Do đó, thể tích tảng băng là:
Thể tıˊch tảng ba˘ng=1 dm3+0.09 dm3=1.09 dm3\text{Thể tích tảng băng} = 1 \, \text{dm}^3 + 0.09 \, \text{dm}^3 = 1.09 \, \text{dm}^3
Phần B: Tính phần trăm thể tích giảm khi tảng băng tan thành nước.
Khi tảng băng tan thành nước, thể tích giảm từ 1.09 đề xi mét khối về 1 đề xi mét khối. Ta tính phần trăm thể tích giảm như sau:
Phaˆˋn tra˘m giảm=Thể tıˊch giảmThể tıˊch ban đaˆˋu của tảng ba˘ng×100%\text{Phần trăm giảm} = \frac{\text{Thể tích giảm}}{\text{Thể tích ban đầu của tảng băng}} \times 100\%
Thể tích giảm là:
Thể tıˊch giảm=1.09 dm3−1 dm3=0.09 dm3\text{Thể tích giảm} = 1.09 \, \text{dm}^3 - 1 \, \text{dm}^3 = 0.09 \, \text{dm}^3
Do đó, phần trăm thể tích giảm là:
Phaˆˋn tra˘m giảm=0.09 dm31.09 dm3×100%≈8.26%\text{Phần trăm giảm} = \frac{0.09 \, \text{dm}^3}{1.09 \, \text{dm}^3} \times 100\% \approx 8.26\%
Vậy, khi tảng băng tan thành nước, thể tích của nó giảm đi khoảng 8.26%.
Kết luận:
- A: Thể tích tảng băng là 1.09 đề xi mét khối.
- B: Khi tảng băng tan thành nước, thể tích của nó giảm đi khoảng 8.26%.

1: Sửa đề: \(f\left(x\right)=3x\left(1-3x+2x^3\right)-2x^2\left(-4+3x^2-x\right)\)
\(=3x-9x^2+6x^4+8x^2-6x^4+2x^3\)
\(=2x^3-x^2+3x\)
\(g\left(x\right)=-4\left(x^4+x^2+1\right)+x^3\left(4x+2\right)+4\)
\(=-4x^4-4x^2-4+4x^3+2x^3+4\)
\(=2x^3-4x^2\)
Bậc là 3
Hệ số cao nhất là 2
Hệ số tự do là 0
2: f(x)=g(x)+h(x)
=>h(x)=f(x)-g(x)
\(=2x^3-x^2+3x-2x^3+4x^2=3x^2+3x\)
3: Đặt h(x)=0
=>3x(x+1)=0
=>x(x+1)=0
=>\(\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
1. `G(x)=-4(x^4+x^2+1)+x^3(4x+2)+4`
`=-4x^4-4x^2-4+4x^4+2x^3+4`
`=(4x^4-4x^4)+2x^3-4x^2+(4-4)`
`=2x^3-4x^2`
Bậc 3
Hệ số cao nhất: 2
Hệ số tự đó: 0
2. `F(x) = G(x) + H(x)`
`=>H(x)=F(x) - G(x)`
`=>H(x)=[3x(1-3x+2x^3)-2x^2(-4+3x^2-x)]-(2x^3-4x^2)
`=>H(x)=3x-9x^2+6x^4+8x^2-6x^4+2x^3-2x^3+4x^2`
`=>H(x)=3x^2+3x`
3. `H(x)=3x^2+3x=0`
`=>3x(x+1)=0`
TH1: `x=0`
TH2: `x+1=0=>x=-1`

BÀI 1:
a) \(\dfrac{9}{70}>\dfrac{5}{42}\) b) \(-\dfrac{4}{27}>-\dfrac{10}{63}\)
c) \(\dfrac{999}{556}>\dfrac{1000}{557}\) d) \(-\dfrac{2}{15}< \dfrac{10}{11}\)
BÀI 2:
\(-1\dfrac{2}{3}< -\dfrac{3}{5}< -\dfrac{5}{9}< 0,5< \dfrac{10}{9}\)
BÀI 3:
a) -3 ϵ Q b) 10 ϵ N
c) -3/7 ϵ Q d) -2 ϵ Q

`(-3^x*3^6)/(-27*9^x) = -3`
`(-3^(x+6))/(-3^3*(3^2)^x)=-3`
`(-3^(x+6))/(-3^3*3^(2x))=-3`
`(-3^(x+6))/(-3^(2x+3))=-3`
`3^(x+6-2x-3)=-3`
`3^(3-x)=-3`
`(3^(3-x))/3=-1`
`3^(3-x-1)=-1`
`3^(2-x)=-1`
Vì `3^(2-x) > 0` mà `-1<0`
Nên không có x thoả mãn

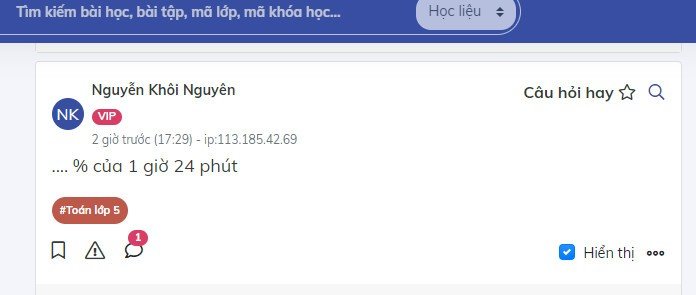
\(x^2-x-2001\cdot2002\)
\(=x^2-2002x+2001x-2001\cdot2002\)
\(=x\left(x-2002\right)+2001\left(x-2002\right)=\left(x-2002\right)\left(x+2001\right)\)