1/1×3+1/3×5+1/5×7+......+1/2021×2023
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{-2}{5}\cdot\dfrac{4}{7}+\dfrac{-3}{5}\cdot\dfrac{2}{7}+\dfrac{-3}{5}\)
\(=\dfrac{-2}{5}\cdot\dfrac{4}{7}+\dfrac{-3}{5}\left(\dfrac{2}{7}+1\right)\)
\(=\dfrac{-2}{5}\cdot\dfrac{4}{7}+\dfrac{-3}{5}\cdot\dfrac{9}{7}\)
\(=\dfrac{-8-27}{35}=\dfrac{-35}{35}=-1\)

\(\dfrac{20}{1\cdot6}+\dfrac{20}{6\cdot11}+...+\dfrac{20}{101\cdot106}\)
\(=4\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{101\cdot106}\right)\)
\(=4\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{101}-\dfrac{1}{106}\right)\)
\(=4\left(1-\dfrac{1}{106}\right)=4\cdot\dfrac{105}{106}=\dfrac{105\cdot2}{53}=\dfrac{210}{53}\)

a: \(\dfrac{4}{13}+\dfrac{-12}{39}=\dfrac{4}{13}-\dfrac{4}{13}=0\)
b: \(\dfrac{27}{23}-\dfrac{-5}{21}-\dfrac{4}{23}+\dfrac{16}{21}+\dfrac{1}{2}\)
\(=\left(\dfrac{27}{23}-\dfrac{4}{23}\right)+\left(\dfrac{5}{21}+\dfrac{16}{21}\right)+\dfrac{1}{2}\)
\(=1+1+\dfrac{1}{2}=\dfrac{5}{2}\)
c: \(\dfrac{-8}{9}+\dfrac{1}{9}\cdot\dfrac{2}{9}+\dfrac{1}{9}\cdot\dfrac{7}{9}\)
\(=\dfrac{-8}{9}+\dfrac{1}{9}\left(\dfrac{2}{9}+\dfrac{7}{9}\right)\)
\(=\dfrac{-8}{9}+\dfrac{1}{9}=\dfrac{-7}{9}\)
d: \(\dfrac{2}{\left(-3\right)^2}+\dfrac{5}{-12}-\dfrac{-3}{4}\)
\(=\dfrac{2}{9}-\dfrac{5}{12}+\dfrac{3}{4}\)
\(=\dfrac{8}{36}-\dfrac{15}{36}+\dfrac{27}{36}=\dfrac{19}{36}\)

- Với \(p=3\Rightarrow8p-1=8.3-1=23\) là số nguyên tố và \(8p+1=25\) là hợp số
- Với \(p\ne3\Rightarrow p\) không chia hết cho 3
\(\Rightarrow p=3k+1\) hoặc \(p=3k+2\)
Với \(p=3k+1\Rightarrow8p+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)\) chia hết cho 3 \(\Rightarrow\) là hợp số
Với \(p=3k+2\Rightarrow8p-1=8\left(3k+2\right)-1=24k+15=3\left(8k+5\right)\) chia hết cho 3 \(\Rightarrow\) là hợp số
Vậy số còn lại luôn là hợp số

\(\dfrac{-2}{7}\cdot\dfrac{7}{4}+\dfrac{-2}{7}\cdot\dfrac{-3}{4}-2\dfrac{1}{7}\)
\(=\dfrac{-2}{7}\left(\dfrac{7}{4}-\dfrac{3}{4}\right)-\dfrac{15}{7}\)
\(=\dfrac{-2}{7}-\dfrac{15}{7}=\dfrac{-17}{7}\)

Lời giải:
Gọi chiều dài và chiều rộng ban đầu là $a$ và $b$ (m)
Theo bài ra ta có:
$(a+36)b.0,84=ab.1,05$
$\Rightarrow b[(a+36).0,84-1,05a]=0$
$\Rightarrow (a+36).0,84-1,05a=0$
$\Rightarrow 30,24=0,21a$
$\Rightarrow a=144$ (m)
Vậy chiều dài mới là: $a+36=144+36=180$ (m)

Bài 2:
a: \(\dfrac{7}{8}+x=\dfrac{3}{5}\)
=>\(x=\dfrac{3}{5}-\dfrac{7}{8}=\dfrac{24-35}{40}=\dfrac{-11}{40}\)
b: \(\dfrac{17}{2}:x=5\)
=>\(x=\dfrac{17}{2}:5\)
=>\(x=\dfrac{17}{2\cdot5}=\dfrac{17}{10}\)
c: \(x-\dfrac{3}{8}=2+\dfrac{1}{4}\)
=>\(x-\dfrac{3}{8}=\dfrac{9}{4}\)
=>\(x=\dfrac{9}{4}+\dfrac{3}{8}=\dfrac{18}{8}+\dfrac{3}{8}=\dfrac{21}{8}\)
d: \(\dfrac{1}{2}+\dfrac{3}{5}\left(x-2\right)=\dfrac{1}{5}\)
=>\(\dfrac{3}{5}\left(x-2\right)=\dfrac{1}{5}-\dfrac{1}{2}=\dfrac{-3}{10}\)
=>\(x-2=-\dfrac{1}{2}\)
=>\(x=2-\dfrac{1}{2}=\dfrac{3}{2}\)
Bài 1:
a: \(\dfrac{-3}{4}+\dfrac{1}{5}=\dfrac{-15}{20}+\dfrac{4}{20}=\dfrac{-15+4}{20}=\dfrac{-11}{20}\)
b: \(\dfrac{-2}{5}-\dfrac{1}{3}=\dfrac{-6}{15}-\dfrac{5}{15}=\dfrac{-6-5}{15}=\dfrac{-11}{15}\)
c: \(\dfrac{3}{7}\cdot\dfrac{2}{5}-\dfrac{2}{5}=\dfrac{2}{5}\left(\dfrac{3}{7}-1\right)=\dfrac{2}{5}\cdot\dfrac{-4}{7}=\dfrac{-8}{35}\)
d: \(\dfrac{1}{4}+\dfrac{3}{4}\left(\dfrac{2}{3}-\dfrac{1}{2}\right)\)
\(=\dfrac{1}{4}+\dfrac{3}{4}\cdot\dfrac{4-3}{6}\)
\(=\dfrac{1}{4}+\dfrac{3}{4}\cdot\dfrac{1}{6}=\dfrac{1}{4}+\dfrac{1}{8}=\dfrac{3}{8}\)
e: \(\dfrac{7}{2}\cdot\dfrac{8}{13}+\dfrac{8}{13}\cdot\dfrac{-5}{12}+\dfrac{8}{13}\)
\(=\dfrac{8}{13}\left(\dfrac{7}{2}-\dfrac{5}{2}+1\right)\)
\(=\dfrac{8}{13}\cdot2=\dfrac{16}{13}\)
f: \(1+\dfrac{1}{8}+\dfrac{1}{24}+\dfrac{1}{48}+\dfrac{1}{80}+\dfrac{1}{120}\)
\(=1+\dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+\dfrac{1}{6\cdot8}+\dfrac{1}{8\cdot10}+\dfrac{1}{10\cdot12}\)
\(=1+\dfrac{1}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{10\cdot12}\right)\)
\(=1+\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{10}-\dfrac{1}{12}\right)\)
\(=1+\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{12}\right)\)
\(=1+\dfrac{1}{2}\cdot\dfrac{5}{12}=1+\dfrac{5}{24}=\dfrac{29}{24}\)

-1/4 + 2/5 . x = 4/15
2/5 . x = 4/15 + 1/4
2/5 . x = 31/60
x = 31/60 : 2/5
x = 31/24
-1/4+2/5.x=4/15
2/5.x=4/15-1/4
2/5.x=1/60
X=1/60:2/5
X=1/60.5/2
X= 1/24
-1/4+2/5.x=4/15

\(\dfrac{8}{9}.-\dfrac{7}{13}-\dfrac{8}{9}.\dfrac{6}{13}+2\dfrac{8}{9}\\ =\dfrac{8}{9}.\left(-\dfrac{7}{13}-\dfrac{6}{13}\right)+\dfrac{26}{9}\\ =\dfrac{8}{9}.-1+\dfrac{26}{9}\\ =-\dfrac{8}{9}+\dfrac{26}{9}\\ =2.\)
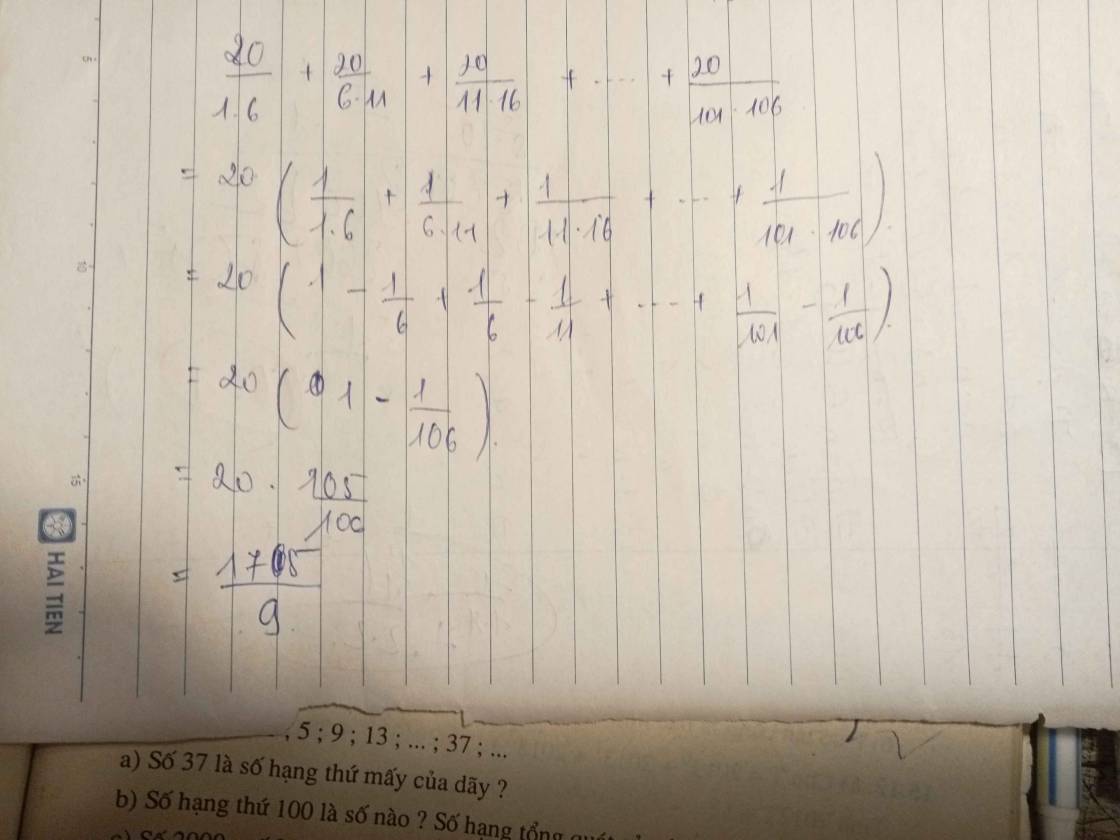
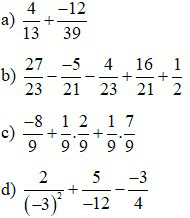
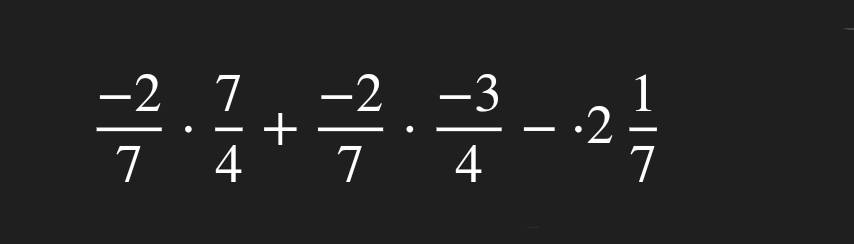
\(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{2021\cdot2023}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2021\cdot2023}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{2023}\right)=\dfrac{1}{2}\cdot\dfrac{2022}{2023}=\dfrac{1011}{2023}\)
=1/1.3+1/3.5+1/5.7+......+1/2021.2023
=1/1-1/3+1/3-1/5+....+1/2021-1/2023
=1/1-1/2023
=1-1/2023
=2023/2023-1/2023
=2022/2023
Đáp án là : 2022/2023
(không bít có đúng không nữa :_3)