Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x-1}{69}+\dfrac{x-2}{68}=\dfrac{x-5}{65}+\dfrac{x-6}{64}\)
\(\Leftrightarrow\left(\dfrac{x-1}{69}-1\right)+\left(\dfrac{x-2}{68}-1\right)-\left(\dfrac{x-5}{65}-1\right)-\left(\dfrac{x-6}{64}-1\right)=0\)
\(\Leftrightarrow\dfrac{x-70}{69}+\dfrac{x-70}{68}-\dfrac{x-70}{65}-\dfrac{x-70}{64}=0\)
\(\Leftrightarrow\left(x-70\right)\left(\dfrac{1}{69}+\dfrac{1}{68}-\dfrac{1}{65}-\dfrac{1}{64}\right)=0\)
\(\Leftrightarrow x-70=0\) (do \(\dfrac{1}{69}+\dfrac{1}{68}-\dfrac{1}{65}-\dfrac{1}{64}\ne0\))
\(\Rightarrow x=70\)

\(P=\left(-\dfrac{1}{7}\right)^0+\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2017}\)
\(\left(-\dfrac{1}{7}\right).P=\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2017}+\left(-\dfrac{1}{7}\right)^{2018}\)
\(P-\left(-\dfrac{1}{7}\right)P=\left(-\dfrac{1}{7}\right)^0-\left(-\dfrac{1}{7}\right)^{2018}\)
\(\dfrac{8}{7}P=1-\dfrac{1}{7^{2018}}\)
\(\dfrac{8}{7}P=\dfrac{7^{2018}-1}{7^{2018}}\)
\(P=\dfrac{7^{2018}-1}{8.7^{2017}}\)

\(a,\left(\dfrac{2}{3}\right)^{x+2}=\dfrac{8}{27}\\ =>\left(\dfrac{2}{3}\right)^{x+2}=\left(\dfrac{2}{3}\right)^3\\ =>x+2=3\\ =>x=3-2\\ =>x=1\\ b,\left(\dfrac{1}{2}\right)^{x+1}=\dfrac{1}{8}\\ =>\left(\dfrac{1}{2}\right)^{x+1}=\left(\dfrac{1}{2}\right)^3\\ =>x+1=3\\ =>x=3-1\\ =>x=2\)

Ta có: \(\left\{{}\begin{matrix}\left|x+1\right|\ge0\\\left(y-2\right)^{2028}\ge0\end{matrix}\right.\)
=> \(\left|x+1\right|+\left(y-2\right)^{2028}\ge0\)
Dấu = xảy ra khi:
\(\left\{{}\begin{matrix}x+1=0\\y-2=0\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
Khi đó:
`A =` \(x^{2024}+\left(5-y\right)^3\)
`=` \(\left(-1\right)^{2024}\) `+ (5-2)^3 `
`= 1 + 3^3 `
`=1 + 27`
`= 28`
Vậy `A = 28`

\(\dfrac{15}{23}-\dfrac{21}{23}-\left(-\dfrac{8}{23}\right)-\left(-\dfrac{21}{33}\right)\)
\(=\left(\dfrac{15}{23}+\dfrac{8}{23}-\dfrac{21}{23}\right)+\dfrac{21}{33}\)
\(=\dfrac{2}{23}+\dfrac{21}{33}=\dfrac{2\cdot33+21\cdot23}{23\cdot33}=\dfrac{549}{759}\)
Sửa đề:
\(\dfrac{15}{23}-\dfrac{21}{23}-\left(-\dfrac{8}{23}\right)-\left(-\dfrac{21}{23}\right)\\ =\dfrac{15}{23}-\dfrac{21}{23}+\dfrac{8}{23}+\dfrac{21}{23}\\ =\left(\dfrac{15}{23}+\dfrac{8}{23}\right)+\left(-\dfrac{21}{23}+\dfrac{21}{23}\right)\\ =1+0\\ =1\)


a: 2x-3=x+1/2
=>\(2x-x=3+\dfrac{1}{2}\)
=>\(x=\dfrac{7}{2}\)
b: \(4x-\left(2x+1\right)=3-\dfrac{1}{3}+x\)
=>\(4x-2x-1=x+\dfrac{8}{3}\)
=>\(2x-1=x+\dfrac{8}{3}\)
=>\(2x-x=\dfrac{8}{3}+1\)
=>\(x=\dfrac{11}{3}\)

\(\dfrac{1}{2}\)\(x^2\) = \(\dfrac{1}{4}x^2\) + \(\dfrac{1}{4}\)\(x^2\)

\(\left(2x-1\right)\left(3x+1\right)+\left(3x+4\right)\left(3x-2\right)=5\)
=>\(6x^2+2x-3x-1+9x^2-6x+12x-8=5\)
=>\(15x^2+5x-9-5=0\)
=>\(15x^2+5x-14=0\)
\(\Delta=5^2-4\cdot15\cdot\left(-14\right)=25+60\cdot14=25+840=865>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{-5-\sqrt{865}}{2\cdot15}=\dfrac{-5-\sqrt{865}}{30}\\x=\dfrac{-5+\sqrt{865}}{30}\end{matrix}\right.\)

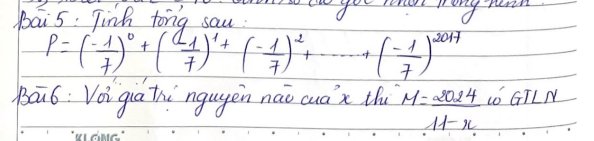
 mn lm giup e vs a
mn lm giup e vs a
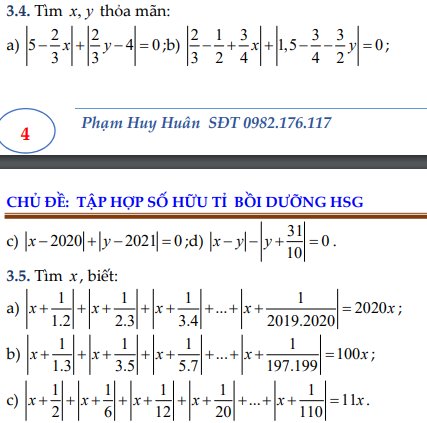
3.4
a) Ta có:
`|5-2/3x|>=0` với mọi x
`|2/3y-4|>=0` với mọi y
`=>|5-2/3x|+|2/3y-4|>=0` với mọi x
Mà: `|5-2/3x|+|2/3y-4|=0`
Dấu "=" xảy ra: `5-2/3x=0` và `2/3y-4=0`
`<=>2/3x=5` và `2/3y=4`
`<=>x=5:2/3=15/2` và `y=4:2/3=6`
b)
`|2/3-1/2+3/4x|+|1,5-3/4-3/2y|=0`
`=>|1/6+3/4x|+|3/4-3/2y|=0`
Ta có:
`|1/6+3/4x|>=0` với mọi x
`|3/4-3/2y|>=0` với mọi y
`=>|1/6+3/4x|+|3/4-3/2y|>=0` với mọi x
Mà: `|1/6+3/4x|+|3/4-3/2y|=0`
Dấu "=" xảy ra: `1/6+3/4x=0` và `3/4-3/2y=0`
`<=>3/4x=-1/6` và `3/2y=3/4`
`<=>x=-1/6:3/4=-2/9` và `y=3/4:3/2=1/2`