ĐKXĐ: x<>2

\(\dfrac{x-2}{50}=\dfrac{2}{x-2}\)

=>\(\left(x-2\right)^2=2\cdot50=100\)

=>\(\left[{}\begin{matrix}x-2=10\\x-2=-10\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=12\left(nhận\right)\\x=-8\left(nhận\right)\end{matrix}\right.\)

Olm chào em. Đây là dạng toán nâng cao chuyên đề tính nhanh tổng các phân số quy luật. Cấu trúc thi chuyên, thi hsg. Hôm nay, Olm.vn sẽ hướng dẫn các em làm dạng này như sau:

                      Giải

A = \(\dfrac{2}{2.4.6}\) + \(\dfrac{2}{4.6.8}\) + ... + \(\dfrac{2}{38.40.42}\)

A = \(\dfrac{2}{2}\).(\(\dfrac{2}{2.4.6}+\dfrac{2}{4.6.8}+...+\dfrac{2}{38.40.42}\))

A = \(\dfrac{1}{2}\).(\(\dfrac{2.2}{2.4.6}+\dfrac{2.2}{4.6.8}+\dfrac{2.2}{38.40.42}\))

A = \(\dfrac{1}{2}\).(\(\dfrac{4}{2.4.6}+\dfrac{4}{4.6.8}+...+\dfrac{4}{38.40.42}\))

A = \(\dfrac{1}{2}\).(\(\dfrac{1}{2.4}\) - \(\dfrac{1}{4.6}\) + \(\dfrac{1}{4.6}\) -  \(\dfrac{1}{6.8}\)+ ... + \(\dfrac{1}{38.40}\) - \(\dfrac{1}{40.42}\))

A = \(\dfrac{1}{2}\).(\(\dfrac{1}{2.4}\) - \(\dfrac{1}{40.42}\))

A = \(\dfrac{1}{2}\).(\(\dfrac{1}{8}\) - \(\dfrac{1}{1680}\))

A = \(\dfrac{1}{2}\).\(\dfrac{209}{1680}\)

A = \(\dfrac{209}{3360}\)

1: \(\dfrac{2}{3}x-\dfrac{1}{2}x=\dfrac{1}{4}\)

=>\(x\left(\dfrac{2}{3}-\dfrac{1}{2}\right)=\dfrac{1}{4}\)

=>\(x\cdot\dfrac{1}{6}=\dfrac{1}{4}\)

=>\(x=\dfrac{1}{4}:\dfrac{1}{6}=\dfrac{6}{4}=\dfrac{3}{2}\)

2: \(\dfrac{3}{x-5}=\dfrac{-4}{x+2}\)

=>-4(x-5)=3(x+2)

=>-4x+20=3x+6

=>-7x=-14

=>x=2(nhận)

làm đc là người có IQ vô cức nhé

nhớ thích nhé 

110/264 và 21/264

rùi đó

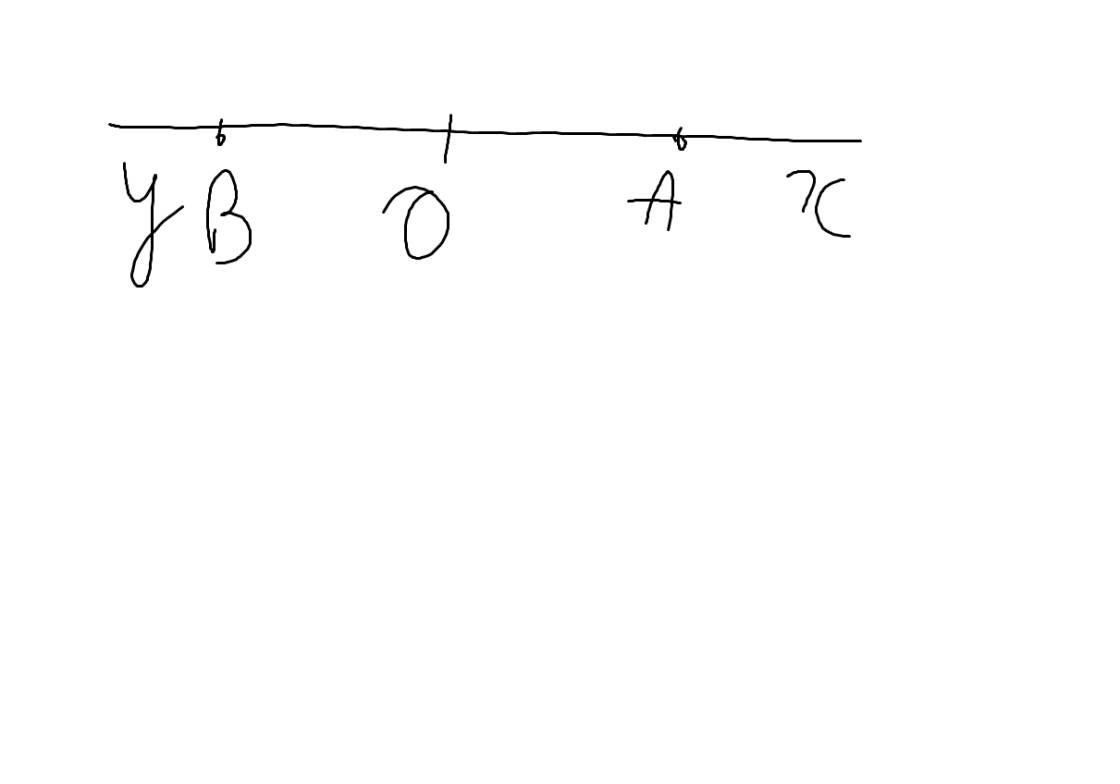
a: Các cặp tia đối nhau gốc O là:
OA và OB

Ox và Oy

Ox và OB

Oy và OA

b: Vì OA và OB là hai tia đối nhau

nên O nằm giữa A và B

=>AB=OA+OB=2+3=5(cm)

khi đó có số cân nặng là : 2,5:92x90=2,445 

(kg)

\(\dfrac{x}{15}+\dfrac{7}{20}=\dfrac{73}{60}\)

=>\(\dfrac{x}{15}=\dfrac{73}{60}-\dfrac{7}{20}=\dfrac{73-21}{60}=\dfrac{52}{60}\)

=>\(\dfrac{x}{15}=\dfrac{13}{15}\)

=>x=13

Giúp câu hỏi này nhanh nhanh nhé ^^

\(\dfrac{7}{8}-x=-\dfrac{3}{5}\)

=>\(x=\dfrac{7}{8}+\dfrac{3}{5}\)

=>\(x=\dfrac{35+24}{40}=\dfrac{59}{40}\)

ĐKXĐ: n<>-2

Để \(\dfrac{2n+7}{n+2}\in Z\) thì \(2n+7⋮n+2\)

=>\(2n+4+3⋮n+2\)

=>\(3⋮n+2\)

=>\(n+2\in\left\{1;-1;3;-3\right\}\)

=>\(n\in\left\{-1;-3;1;-5\right\}\)