Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với \(n=0\) thì đpcm thành \(0⋮30\), luôn đúng.
Với \(n=1\) thì đpcm thành \(x^5-x⋮30\). Ta thấy:
\(VT=x^5-x=x\left(x^4-1\right)=x\left(x^2-1\right)\left(x^2+1\right)=x\left(x-1\right)\left(x+1\right)\left(x^2+1\right)\)
Ta thấy \(x\left(x-1\right)\left(x+1\right)\) là tích của 3 số liên tiếp nên nó chia hết cho 6 \(\Rightarrow VT⋮6\) (1)
Nếu \(x⋮5\Rightarrow VT⋮5\)
Nếu \(x\equiv\pm1\left[5\right]\) thì \(x-1\) hoặc \(x+1\) chia hết cho 5 \(\Rightarrow VT⋮5\)
Nếu \(x\equiv\pm2\left[5\right]\) thì \(x^2+1⋮5\Rightarrow VT⋮5\)
Vậy với mọi \(x\) thì \(VT⋮5\) (2)
Do \(ƯCLN\left(5,6\right)=1\) nên từ (1) và (2) \(\Rightarrow x^5-x⋮30\)
Vậy với \(n=1\) thì khẳng định đúng.
Giả sử khẳng định đúng đến \(n=k\ge0\). Ta cần chứng minh khẳng định đúng với \(n=k+1\)
Với \(n=k+1\), ta có:
\(x^{4n+1}-x\) \(=x^{4\left(k+1\right)+1}-x\)
\(=x^{4k+5}-x\)
\(=x^4.x^{4k+1}-x^5+x^5-x\)
\(=x^4\left(x^{4k+1}-x\right)+\left(x^5-x\right)\)
Mà theo giả thiết quy nạp, \(x^{4k+1}-x⋮30\) và theo cmt thì \(x^5-x⋮30\)
\(\Rightarrow x^{4n+1}-x=x^4\left(x^{4k+1}-x\right)+\left(x^5-x\right)⋮30\). Như vậy, khẳng định đúng với \(n=k+1\).
Theo nguyên lí quy nạp, ta có đpcm.

b) Để ý rằng phương trình của trục Ox là \(y=0\). Do đó pt hoành độ giao điểm của Ox và d là \(\left(m^2+1\right)x_A-2m=0\Leftrightarrow x_A=\dfrac{2m}{m^2+1}\)
Mà \(OA=\left|x_A\right|=\left|\dfrac{2m}{m^2+1}\right|=\dfrac{2\left|m\right|}{m^2+1}\) , \(OA=\dfrac{4}{5}\)
\(\Rightarrow\dfrac{2\left|m\right|}{m^2+1}=\dfrac{4}{5}\)
\(\Leftrightarrow2m^2-5\left|m\right|+2=0\)
Xét \(m\ge0\), khi đó \(2m^2-5m+2=0\Leftrightarrow\left[{}\begin{matrix}m=2\\m=\dfrac{1}{2}\end{matrix}\right.\) (nhận)
Xét \(m< 0\), khi đó \(2m^2+5m+2=0\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{1}{2}\\m=-2\end{matrix}\right.\) (nhận)
Vậy \(m\in\left\{\pm2;\pm\dfrac{1}{2}\right\}\) thỏa mãn ycbt.
c) Theo câu b), ta có \(OA=\dfrac{2\left|m\right|}{m^2+1}\). d cắt Oy tại \(B\left(0,-2m\right)\)
\(\Rightarrow OB=\left|-2m\right|=2\left|m\right|\)
Có \(OA=2OB\Leftrightarrow\dfrac{2\left|m\right|}{m^2+1}=4\left|m\right|\)
\(\Leftrightarrow\left|m\right|\left(2-\dfrac{1}{m^2+1}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\2m^2+1=0\left(vôlý\right)\end{matrix}\right.\)
Vậy \(m=0\) thỏa mãn ycbt.
d) Gọi \(h\) là khoảng cách từ O đến d thì khi đó:
\(\dfrac{1}{h^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)
\(=\dfrac{1}{\left(\dfrac{2\left|m\right|}{m^2+1}\right)^2}+\dfrac{1}{\left(2\left|m\right|\right)^2}\)
\(=\dfrac{m^4+2m^2+1}{4m^2}+\dfrac{1}{4m^2}\)
\(=\dfrac{m^4+2m^2+2}{4m^2}\)
\(\Rightarrow h^2=\dfrac{4m^2}{m^4+2m^2+2}\)
Đặt \(t=m^2\left(t>0\right)\) thì ta có \(h^2=\dfrac{4t}{t^2+2t+2}=P\)
\(\Leftrightarrow Pt^2+2\left(P-2\right)t+2P=0\) (*)
Có \(\Delta'=\left(P-2\right)^2-2P^2=P^2-4P+4-2P^2=-P^2-4P+4\)
\(\Delta'\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Ta thấy \(P=\dfrac{2P}{P}=2>0\) nên để pt đã cho có 1 nghiệm dương thì \(S>0\Leftrightarrow-2\left(P-2\right)>0\Leftrightarrow P< 2\)
Kết hợp 2 điều kiện, ta được \(-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(maxP=-2+2\sqrt{2}\). Dấu "=" xảy ra khi \(t=\dfrac{-2\left(-2+2\sqrt{2}-2\right)}{2\left(-2+2\sqrt{2}\right)}=\sqrt{2}\)
\(\Leftrightarrow m^2=\sqrt{2}\Leftrightarrow m=\pm\sqrt[4]{2}\)
Vậy \(m=\pm\sqrt[4]{2}\) thỏa mãn ycbt.

ĐKXĐ: \(x\notin\left\{0;-20\right\}\)
\(\dfrac{100}{x}-\dfrac{100}{x+20}=\dfrac{5}{12}\)
=>\(\dfrac{20}{x}-\dfrac{20}{x+20}=\dfrac{1}{12}\)
=>\(\dfrac{20\left(x+20\right)-20x}{x\left(x+20\right)}=\dfrac{1}{12}\)
=>\(\dfrac{400}{x\left(x+20\right)}=\dfrac{1}{12}\)
=>\(x\left(x+20\right)=400\cdot12=4800\)
=>\(x^2+20x-4800=0\)
=>(x+80)(x-60)=0
=>\(\left[{}\begin{matrix}x+80=0\\x-60=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-80\left(nhận\right)\\x=60\left(nhận\right)\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne1\end{matrix}\right.\)
\(\dfrac{2}{\sqrt{x}-1}+\dfrac{2\left(\sqrt{x}+1\right)}{x+\sqrt{x}+1}+\dfrac{x-10\sqrt{x}+3}{\sqrt{x^3}-1}\)
\(=\dfrac{2\left(x+\sqrt{x}+1\right)+2\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{x-10\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{2x+2\sqrt{x}+2+2\left(x-1\right)+x-10\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{3x-8\sqrt{x}+5+2x-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{5x-8\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(5\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{5\sqrt{x}-3}{x+\sqrt{x}+1}\)
\(\dfrac{2}{\sqrt{x}-1}+\dfrac{2\left(\sqrt{x}+1\right)}{x+\sqrt{x}+1}+\dfrac{x-10\sqrt{x}+3}{\sqrt{x^3}-1}\left(x\ne1,x>=0\right)\\ =\dfrac{2}{\sqrt{x}-1}+\dfrac{2\left(\sqrt{x}+1\right)}{x+\sqrt{x}+1}+\dfrac{x-10\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{2\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{x-10\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{2x+2\sqrt{x}+2+2\left(x-1\right)+x-10\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{5x-8\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{5x-5\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{\left(\sqrt{x}-1\right)\left(5\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{5\sqrt{x}-3}{x+\sqrt{x}+1}\)

Tùy nha bạn
Lên lớp 10 cái đó được tính vào phần toán đại đấy

a: \(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\9x+3y=27\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+3y-x-3y=27-11\\x+3y=11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x=16\\3y=11-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{11-x}{3}=\dfrac{11-2}{3}=\dfrac{9}{3}=3\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+10y-3x=-1\\2x+4-3x+15y=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y=-1\\-x+15y=-16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\-2x+30y=-32\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y-2x+30y=-1+\left(-32\right)\\x-15y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}40y=-33\\x=15y+16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=15\cdot\dfrac{-33}{40}+16=\dfrac{29}{8}\end{matrix}\right.\)
a)
\(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x+9y=33\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}8y=24\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\3x+3=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3\\x=\dfrac{6}{3}=2\end{matrix}\right.\)
b)
\(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x+10y=3x-1\\2x+4=3x-15y-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\2x-30y=32\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}40y=-33\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x+\dfrac{99}{8}=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=16-\dfrac{99}{8}=\dfrac{29}{8}\end{matrix}\right.\)

\(\dfrac{x+100}{4}+\dfrac{x+99}{5}=\dfrac{x+98}{6}+\dfrac{x+97}{7}\)
=>\(\left(\dfrac{x+100}{4}+1\right)+\left(\dfrac{x+99}{5}+1\right)=\left(\dfrac{x+98}{6}+1\right)+\left(\dfrac{x+97}{7}+1\right)\)
=>\(\dfrac{x+104}{4}+\dfrac{x+104}{5}=\dfrac{x+104}{6}+\dfrac{x+104}{7}\)
=>\(\left(x+104\right)\left(\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}-\dfrac{1}{7}\right)=0\)
=>x+104=0
=>x=-104
\(\dfrac{x+100}{4}+\dfrac{x+99}{5}=\dfrac{x+98}{6}+\dfrac{x+97}{7}\\ \dfrac{x+100}{4}+\dfrac{x+99}{5}-\dfrac{x+98}{6}-\dfrac{x+97}{7}=0\\ \left(\dfrac{x+100}{4}+1\right)+\left(\dfrac{x+99}{5}+1\right)-\left(\dfrac{x+98}{6}+1\right)-\left(\dfrac{x+97}{7}+1\right)=0\\ \dfrac{x+104}{4}+\dfrac{x+104}{5}-\dfrac{x+104}{6}-\dfrac{x+104}{7}=0\\ \left(x+104\right)\cdot\left(\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}-\dfrac{1}{7}\right)=0\)
Vì \(\left(\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}-\dfrac{1}{7}\right)\ne0\) nên:
\(x+104=0\\ x=-104\)
Vậy \(x=-104\)

Thay x=-2 và y=3 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2a\cdot\left(-2\right)+3b\cdot3=5\\-3a\cdot\left(-2\right)+2b\cdot3=30\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-4a+9b=5\\6a+6b=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-12a+27b=15\\12a+12b=60\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-12a+27b+12a+12b=15+60\\a+b=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}39b=75\\a=5-b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{75}{39}=\dfrac{25}{13}\\a=5-\dfrac{25}{13}=\dfrac{40}{13}\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x+2y=1+3\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\7y=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2=4\\y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=4-2=2\\y=1\end{matrix}\right.\)
Vậy: ...
\(\left\{{}\begin{matrix}x+2y=1+3\\2x-3y=1\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x+4y-\left(2x-3y\right)=8-1\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}2x+4y=8\\2x+4y-2x+3y=7\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}2x+4y=8\\\left(2x-2x\right)+\left(4y+3y\right)=7\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}2x+4y=8\\0+7y=7\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}2x+4y=8\\y=1\end{matrix}\right.\)
Thay y = 1 vào biểu thức 2\(x\) + 4y = 8 ta có: 2\(x\) + 4.1 = 8
⇒ 2\(x\) + 4 = 8 ⇒ 2\(x\) = 4 ⇒ \(x\) = 4: 2 ⇒ \(x\) = 2
Vậy \(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
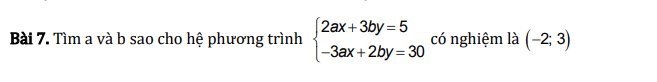
Ta có:
\(a^3+b^3+c^3=3abc\\\Leftrightarrow a^3+b^3+c^3-3abc=0\\\Leftrightarrow (a+b)^3+c^3-3ab(a+b)-3abc=0\\\Leftrightarrow (a+b+c)^3-3(a+b)c(a+b+c)-3ab(a+b+c)=0\\\Leftrightarrow (a+b+c)[(a+b+c)^2-3(a+b)c-3ab]=0\\\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca-3ca-3bc-3ab=0(\text{vì }a+b+c\ne 0)\\\Leftrightarrow a^2+b^2+c^2-ab-bc-ca=0\\\Leftrightarrow 2a^2+2b^2+2c^2-2ab-2bc-2ca=0\\\Leftrightarrow (a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ca+a^2)=0\\\Leftrightarrow(a-b)^2+(b-c)^2+(c-a)^2=0\)
Ta thấy: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\forall a,b\\\left(b-c\right)^2\ge0\forall b,c\\\left(c-a\right)^2\ge0\forall c,a\end{matrix}\right.\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\forall a,b,c\)
Mà: \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Do đó: \(\left\{{}\begin{matrix}a-b=0\\b-c=0\\c-a=0\end{matrix}\right.\Rightarrow a=b=c\)
Khi đó:
\(\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\left(\dfrac{1}{b}+\dfrac{1}{c}\right)\left(\dfrac{1}{c}+\dfrac{1}{a}\right)=\dfrac{2}{a}\cdot\dfrac{2}{b}\cdot\dfrac{2}{c}=\dfrac{8}{abc}\) (đpcm)
#$\mathtt{Toru}$