muốn tính chu vi và diện tích hình thang ta làm thế nào ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng tuổi của mẹ Hà và Hà là:
2 x 25 = 50 (tuổi)
Mà mẹ Hà gấp 4 lần tuổi Hà nên ta coi tuổi mẹ Hà là 4 phần còn tuổi Hà là 1 phần
Tổng số phần bằng nhau là:
1 + 4 = 5 (phần)
Tuổi mẹ Hà là:
50 : 5 x 4 = 40 (tuổi)
Tuổi Hà là:
50 - 40 = 10 (tuổi)
ĐS: ...
Tổng số tuổi của 2 người là: 25x2=50(tuổi)
Tuổi mẹ là \(50\times\dfrac{4}{4+1}=40\left(tuổi\right)\)
Tuổi Hà là 50-40=10(tuổi)


a: Ta có: \(AK=KB=\dfrac{AB}{2}\)
\(DI=IC=\dfrac{DC}{2}\)
mà AB=CD
nên AK=KB=DI=IC
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AI//CK và AI=CK
b: Xét ΔDNC có
I là trung điểm của DC
IM//NC
Do đó: M là trung điểm của DN
=>DM=MN
Xét ΔBAM có
K là trung điểm của BA
KN//AM
Do đó: N là trung điểm của BM
=>BN=NM
=>BN=NM=DM
c: Xét tứ giác BKDI có
BK//DI
BK=DI
Do đó: BKDI là hình bình hành
=>DK//BI
=>EK//FI
ta có: AI//CK
=>IE//KF
Xét tứ giác EKFI có
EK//FI
EI//KF
Do đó: EKFI là hình bình hành

Ta có số đó góc D, E, F của tam giác DEF tỉ lệ nghịch với 2, 3, 6 nên ta có:
\(2\widehat{D}=3\widehat{E}=6\widehat{F}\\ \Rightarrow\dfrac{2\widehat{D}}{12}=\dfrac{3\widehat{E}}{12}=\dfrac{\widehat{6F}}{12}\\ \Rightarrow\dfrac{\widehat{D}}{6}=\dfrac{\widehat{E}}{4}=\dfrac{\widehat{F}}{2}\)
Mà: \(\widehat{D}+\widehat{E}+\widehat{F}=180^o\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{\widehat{D}}{6}=\dfrac{\widehat{E}}{4}=\dfrac{\widehat{F}}{2}=\dfrac{\widehat{D}+\widehat{E}+\widehat{F}}{6+4+2}=\dfrac{180^o}{12}=15^o\)
\(\Rightarrow\widehat{D}=6\cdot15^o=90^o;\widehat{E}=15^o\cdot4=60^o;\widehat{F}=2\cdot15^o=30^o\)
Gọi số đo 3 góc D,E,F của ΔDEF lần lượt là \(d;e;f\) (o)
Điều kiện: \(d;e;f>0\)
Ta có:
+) \(d+e+f=180\) (theo định lý)
+) \(d;e;f\) tỉ lệ nghịch với 2,3,6 nên:
\(2d=3e=6f\)
\(\Rightarrow\dfrac{2d}{6}=\dfrac{3e}{6}=\dfrac{6f}{6}\)
\(\Rightarrow\dfrac{d}{3}=\dfrac{e}{2}=\dfrac{f}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau kết hợp \(d+e+f=180\) được:
\(\dfrac{d}{3}=\dfrac{e}{2}=\dfrac{f}{1}=\dfrac{d+e+f}{3+2+1}=\dfrac{180}{6}=30\)
Do đó:
\(\left\{{}\begin{matrix}d=3\cdot30=90\\e=2\cdot30=60\\f=1\cdot30=30\end{matrix}\right.\) (thỏa mãn điều kiện)
Vậy số đo 3 góc D,E,F của ΔDEF lần lượt là 90o;60o;30o

Gọi vận tốc xe tải là: `x` (km/h)
ĐK: x>0
Khi đó vận tốc của xe khách là: `x+15`(km/h)
Lúc xe tải xuất phát thì khoảng cách giữa 2 xe lúc đó là: \(170-\dfrac{5}{3}\left(x+15\right)=170-\dfrac{5}{3}x-25=145-\dfrac{5}{3}x\left(km\right)\)
Lúc gặp nhau thì xe tải đã đi đc: \(\dfrac{2}{3}x\left(km\right)\)
Lúc gặp nhau thì xe khách đã đi thêm đc: \(\dfrac{2}{3}\left(x+15\right)\left(km\right)\)
Ta có pt:
\(\dfrac{2}{3}x+\dfrac{2}{3}\left(x+15\right)=145-\dfrac{5}{3}x\\ \Leftrightarrow\dfrac{2}{3}x+\dfrac{2}{3}x+10=145-\dfrac{5}{3}x\\ \Leftrightarrow\dfrac{4}{3}x+10=145-\dfrac{5}{3}x\\ \Leftrightarrow\dfrac{4}{3}x+\dfrac{5}{3}x=145-10\\ \Leftrightarrow3x=135\\ \Leftrightarrow x=\dfrac{135}{3}=45\left(tm\right)\)
Vận tốc xe khách là 45 + 15 = 60 (km/h)
Gọi vận tốc xe khách, xe tải lần lượt là a ;b ( a;b>0)
xe khách đi nhanh hơn xe tải 15 km/h => a = b + 15
xe khách đi được 5/3 giờ, xe tải bắt đầu xuất phát 2/3 giờ thì gặp nhau
\(\dfrac{7}{3}a+\dfrac{2}{3}b=170\)
\(\left\{{}\begin{matrix}a-b=15\\\dfrac{7}{3}a+\dfrac{2}{3}b=170\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=60\\b=45\end{matrix}\right.\)km/h

a) 4,5 x 5,3 + 4,7 x 4,5
= 4,5 x (5,3 + 4,7)
= 4,5 x 10
= 45
b) 73,5 x 35,64 - 73,5 x 64,37
= 73,5 x (35,64 - 64,37)
= 73,5 x -28,73
= -2111,655
c)
\(\dfrac{2007\times2006-8}{2005\times2007+1999}\\ =\dfrac{2007\times\left(2005+1\right)-8}{2007\times2005+1999}\\ =\dfrac{2007\times2005+2007-8}{2007\times2005+1999}\\ =\dfrac{2007\times2005+1999}{2007\times2005+1999}\\ =1\)
a) \(4,5\times5,3+4,7\times4,5\)
\(=4,5\times\left(5,3+4,7\right)\)
\(=4,5\times10\)
\(=45\)
b) Sửa đề: \(73,5\times35,63+73,5\times64,37\)
\(=73,5\times\left(35,63+64,37\right)\)
\(=73,5\times100\)
\(=7350\)
c) Sửa đề: \(\dfrac{2007\times2006-8}{2005\times2007+1999}\)
\(=\dfrac{2007\times2005+2007-8}{2007\times2005+1999}\)
\(=\dfrac{2007\times2005+1999}{2007\times2005+1999}\)
\(=1\)

Câu 25:
\(0< \alpha< \dfrac{\Omega}{2}\)
=>\(0< sin\alpha< 1;0< cos\alpha< 1\)
\(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\)
\(=\dfrac{1+sin\alpha+1-sin\alpha}{cos\alpha}=\dfrac{2}{cos\alpha}\)
Câu 28:
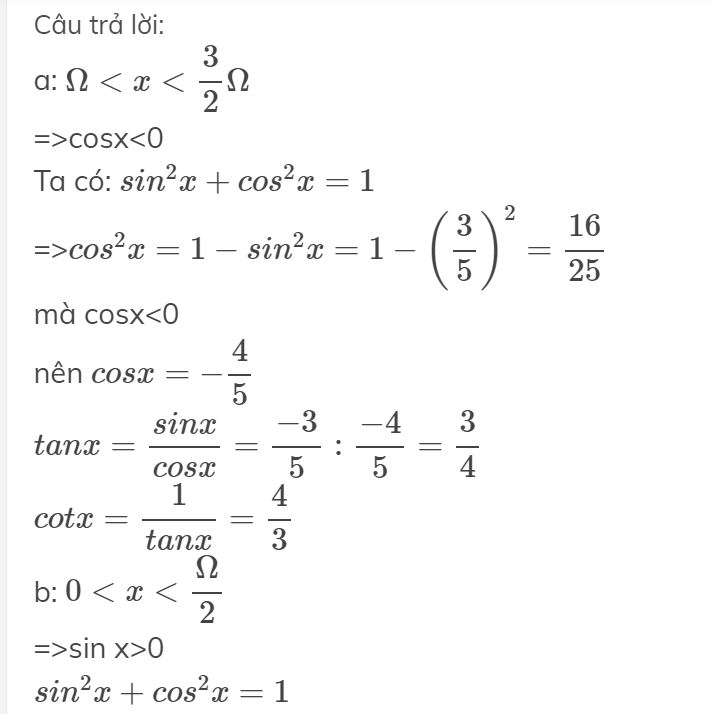


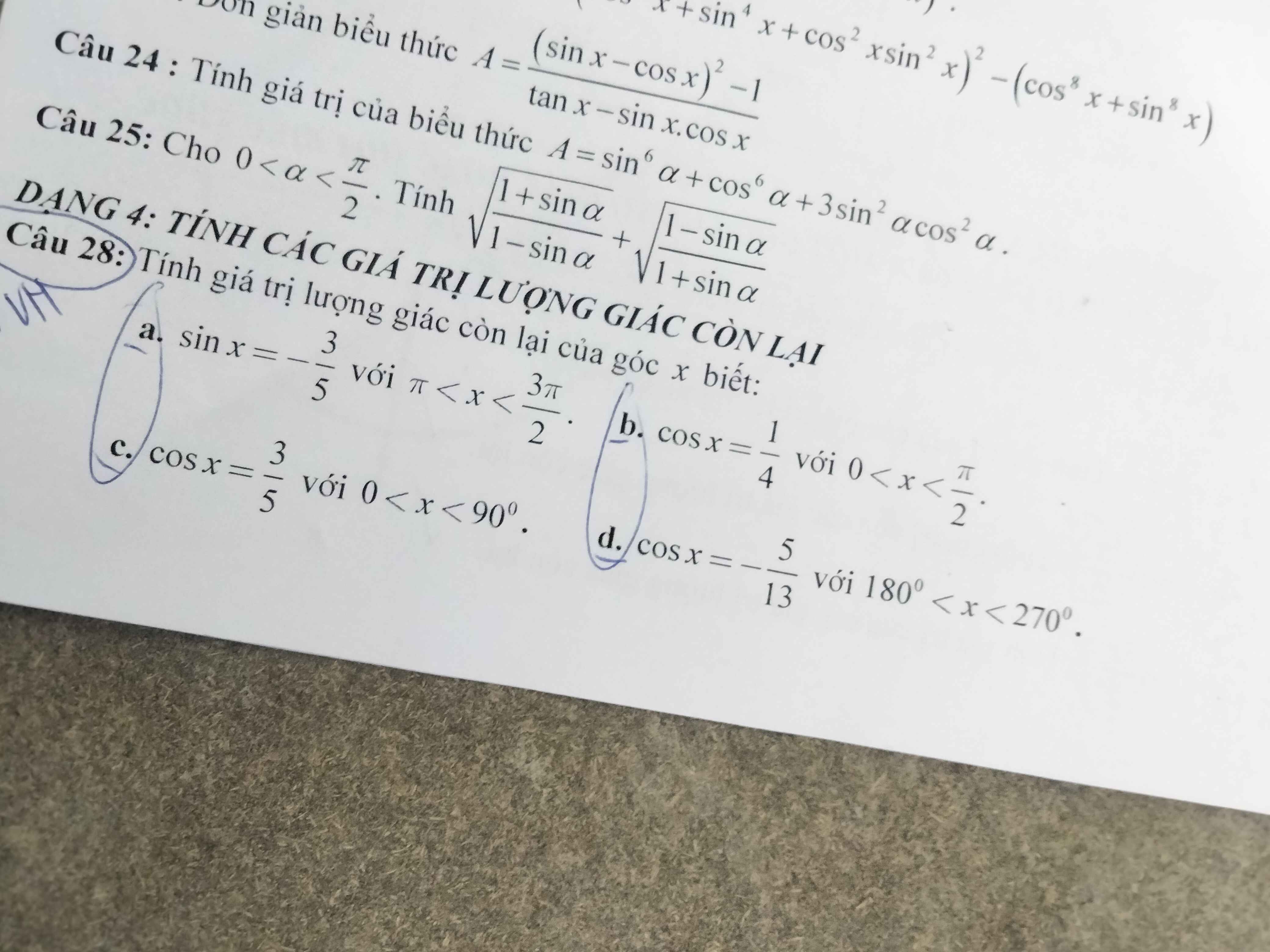
Chu vi:
Ta cộng độ dài của 4 cạnh của hình thang
Diện tích
\(S_{thang}=\dfrac{1}{2}\cdot\left(a+b\right)\cdot h\)
(bằng trung bình cộng 2 đáy nhân với chiều cao)
(đáy lớn + đáy bé) x chiều cao : 2