Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ví dụ giải sơ đồ ven nhé
Ví dụ 1. Đội tuyển thi đá cầu và đấu cờ vua của Trường Tiểu học Võ Thị Sáu có 22 em, trong đó có 15 em thi đá cầu và 12 em thi đấu cờ vua. Hỏi có bao nhiêu em trong đội tuyển thi đấu cả hai môn ?
Giải:
Dựa vào hình vẽ, ta thấy số em chỉ thi đá cầu là:
22 – 12 = 10 (em)
Số em trong đội tuyển thi đấu cả hai môn là:
15 – 10 = 5 (em)
Đáp số: 5 em

Đổi 1 tuần 2 ngày = 9 ngày; 1 tuần 3 ngày = 10 ngày
Tổng số ngày bạn Bình đến thăm ông bà nội và ông bà ngoại là:
\(9+10=19\) (ngày)
Đáp số: 19 ngày

Gọi số xe của đội thứ nhất, thứ hai, thứ ba lần lượt là x,y,z (xe)
Điều kiện: \(x,y,z\inℕ^∗\)
Ta có:
+) Vì đội thứ nhất nhiều hơn đội thứ ba là 10 xe nên:
\(x-z=10\)
+) Vì cùng một lượng hàng hóa thì số xe chở tỉ lệ nghịch với thời gian chở nên:
\(2x=2,5y=3z\Rightarrow\dfrac{2x}{30}=\dfrac{2,5y}{30}=\dfrac{3z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{12}=\dfrac{z}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau kết hợp \(x-z=10\) được:
\(\dfrac{x}{15}=\dfrac{y}{12}=\dfrac{z}{10}=\dfrac{x-z}{15-10}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}x=15\cdot2=30\\y=12\cdot2=24\\z=10\cdot2=20\end{matrix}\right.\) (thỏa mãn điều kiện)
Vậy...

a: \(-\left(2x-4\right)\left(x+2\right)+\left(x+2\right)^2+\left(x-2\right)^2-4x^2-1-4x=-3\)
=>\(-2\left(x^2-4\right)+x^2+4x+4+x^2-4x+4-4x^2-1-4x=-3\)
=>\(-2x^2+8-2x^2-4x+7+3=0\)
=>\(-4x^2-4x+18=0\)
=>\(x=\dfrac{-1\pm\sqrt{19}}{2}\)
b: \(\left(4x-1\right)^2-16\left(x+1\right)\left(x+3\right)=25\)
=>\(16x^2-8x+1-16\left(x^2+4x+3\right)-25=0\)
=>\(16x^2-8x-24-16x^2-64x-48=0\)
=>-72x-72=0
=>x=-1
c: \(\left(3x-7\right)^2=9\left(3x-7\right)\left(x+5\right)+694\)
=>\(9\left(3x^2+15x-7x-35\right)+694=9x^2-42x+49\)
=>\(27x^2+72x-315+694-9x^2+42x-49=0\)
=>\(18x^2+114x+330=0\)
=>\(x\in\varnothing\)
d: \(\left(2x-1\right)^2+\left(x+3\right)^2=5\left(x+7\right)\left(x-7\right)-3x\)
=>\(4x^2-4x+1+x^2+6x+9=5\left(x^2-49\right)-3x\)
=>\(5x^2+2x+10-5x^2+245+3x=0\)
=>5x+255=0
=>x+51=0
=>x=-51

- Cách 1: $A=\{17;18;19;20;21;22;23\}$
- Cách 2: $A=\{x\in \mathbb{N}^*|17< x\le 23\}$
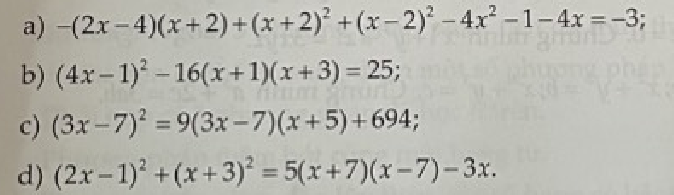
a) $-(2x-4)(x+2)+(x+2)^2+(x-2)^2-4x^2-1-4x=-3$
$\Leftrightarrow (x-2)^2-2(x-2)(x+2)+(x+2)^2-4x^2-4x+2=0$
$\Leftrightarrow (x-2+x+2)^2-4x^2-4x+2=0$
$\Leftrightarrow (2x)^2-4x^2-4x=-2$
$\Leftrightarrow -4x=-2$
$\Leftrightarrow x=\frac12$
b) $(4x-1)^2-16(x+1)(x+3)=25$
$\Leftrightarrow (4x)^2-2.4x.1+1^2-16(x^2+4x+3)=25$
$\Leftrightarrow 16x^2-8x+1-16x^2-64x-48=25$
$\Leftrightarrow -72x-47=25$
$\Leftrightarrow -72x=72$
$\Leftrightarrow x=-1$
c) $(3x-7)^2=9(3x-7)(x+5)+694$
$\Leftrightarrow (3x)^2-2.3x.7+7^2=9(3x^2+8x-35)+694$
$\Leftrightarrow 9x^2-42x+49=27x^2+72x-315+694$
$\Leftrightarrow 18x^2+114x+330=0$
$\Leftrightarrow 9x^2+57x+165=0$
$\Leftrightarrow 9\left(x+\frac{19}{6}\right)^2+\frac{299}{4}=0$ (vô lí)
=> Pt vô nghiệm
d) $(2x-1)^2+(x+3)^2=5(x+7)(x-7)-3x$
$\Leftrightarrow 4x^2-4x+1+x^2+6x+9=5(x^2-49)-3x$
$\Leftrightarrow 5x^2+2x+10=5x^2-3x-245$
$\Leftrightarrow 5x=-255$
$\Leftrightarrow x=-51$
#$\mathtt{Toru}$