A=1x2+2x3+3x4+...+49x50 tính tổng a
B=\(\dfrac{2n-3}{n-1}\)tìm n để b nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(-\dfrac{3}{8}+\dfrac{5}{12}=-\dfrac{9}{24}+\dfrac{10}{24}=\dfrac{1}{24}\)

`#3107.101107`
`j)`
\(1\dfrac{3}{4}-x=\dfrac{-3}{16}+\dfrac{7}{16}\\ \Rightarrow1\dfrac{3}{4}-x=\dfrac{4}{16}\\ \Rightarrow1\dfrac{3}{4}-x=\dfrac{1}{4}\\ \Rightarrow x=1\dfrac{3}{4}-\dfrac{1}{4}\\ \Rightarrow x=\dfrac{3}{2}\)
Vậy, `x =`\(\dfrac{3}{2}.\)
\(1\dfrac{3}{4}-x=\dfrac{-3}{16}+\dfrac{7}{16}\)
=>\(\dfrac{7}{4}-x=\dfrac{1}{4}\)
=>\(x=\dfrac{7}{4}-\dfrac{1}{4}=\dfrac{6}{4}=\dfrac{3}{2}\)

a: Số bài đạt điểm giỏi là \(40\cdot\dfrac{1}{4}=10\left(bài\right)\)
Số bài còn lại là 40-10=30(bài)
Số bài đạt điểm khá là \(30\cdot\dfrac{3}{5}=18\left(bài\right)\)
Số bài đạt điểm trung bình là 30-18=12(bài)
b: Số học sinh giỏi chiếm:
\(\dfrac{10}{40}=25\%\)

a: Các tia đối nhau là Ax và Ay; Ax và AB
Các tia trùng nhau là Ay và AB
b: Hai tia không có điểm chung là By và Ax

Đặt \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2024}}\)
=>\(2A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{2023}}\)
=>\(2A-A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{2023}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{2024}}\)
=>\(A=1-\dfrac{1}{2^{2024}}\)
\(223-x\cdot\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2024}}\right):\left(1-\dfrac{1}{2^{2024}}\right)=23\)
=>\(223-x\left(1-\dfrac{1}{2^{2024}}\right):\left(1-\dfrac{1}{2^{2024}}\right)=23\)
=>223-x=23
=>x=200

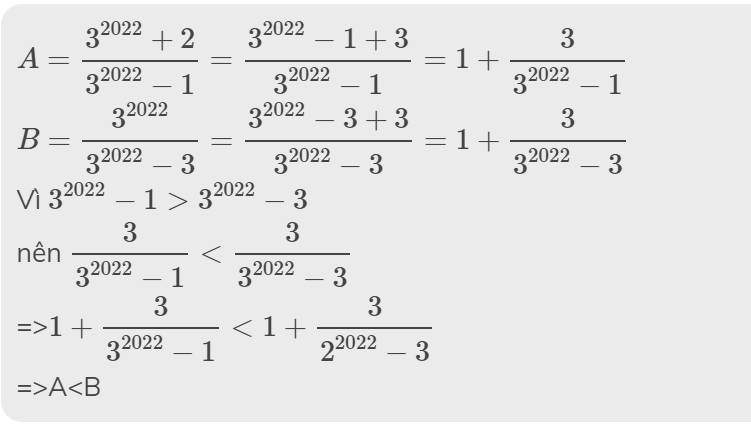
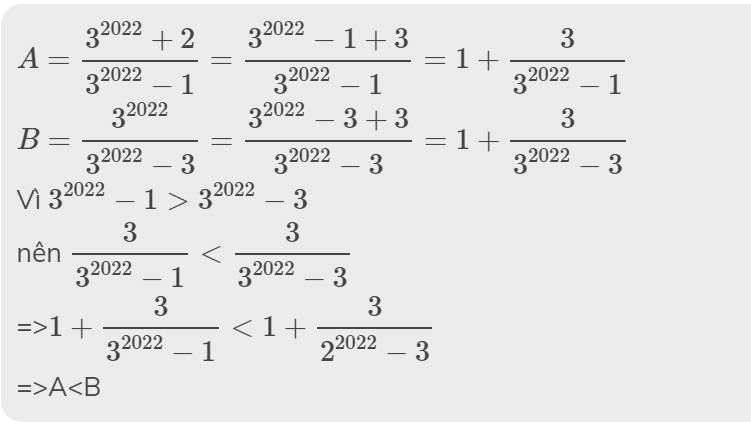
\(A=\dfrac{3^{2022}+2}{3^{2022}-1}=\dfrac{3^{2022}-1+3}{3^{2022}-1}=1+\dfrac{3}{3^{2022}-1}\)
\(B=\dfrac{3^{2022}}{3^{2022}-3}=\dfrac{3^{2022}-3+3}{3^{2022}-3}=1+\dfrac{3}{3^{2022}-3}\)
Vì \(3^{2022}-1>3^{2022}-3\)
nên \(\dfrac{3}{3^{2022}-1}< \dfrac{3}{3^{2022}-3}\)
=>\(1+\dfrac{3}{3^{2022}-1}< 1+\dfrac{3}{2^{2022}-3}\)
=>A<B

Với các số dương \(a;b;n\) sao cho \(a>b\) ta luôn có: \(\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
Thật vậy, do \(a>b\Rightarrow an>bn\Rightarrow ab+an>ab+bn\)
\(\Rightarrow a\left(b+n\right)>b\left(a+n\right)\)
\(\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
Áp dụng:
Do \(3^{2022}>3^{2022}-3>0\) và \(2>0\) nên:
\(\dfrac{3^{2022}}{3^{2022}-3}>\dfrac{3^{2022}+2}{3^{2022}-3+2}\Rightarrow\dfrac{3^{2022}}{3^{2022}-3}>\dfrac{3^{2022}+2}{3^{2022}-1}\)
Vậy \(B>A\)

\(P=\left(a^2+b\right)-\left(2a^2+b\right)+2\left(ab+2021b\right)\)
\(=a^2+b-2a^2-b+2ab+2\cdot2021b\)
\(=-a^2+2ab+2\cdot b\left(a-2b\right)\)
\(=-a^2+2ab+2ba-4b^2\)
\(=-\left(a^2-4ab+4b^2\right)\)
\(=-\left(a-2b\right)^2=-2021^2\)
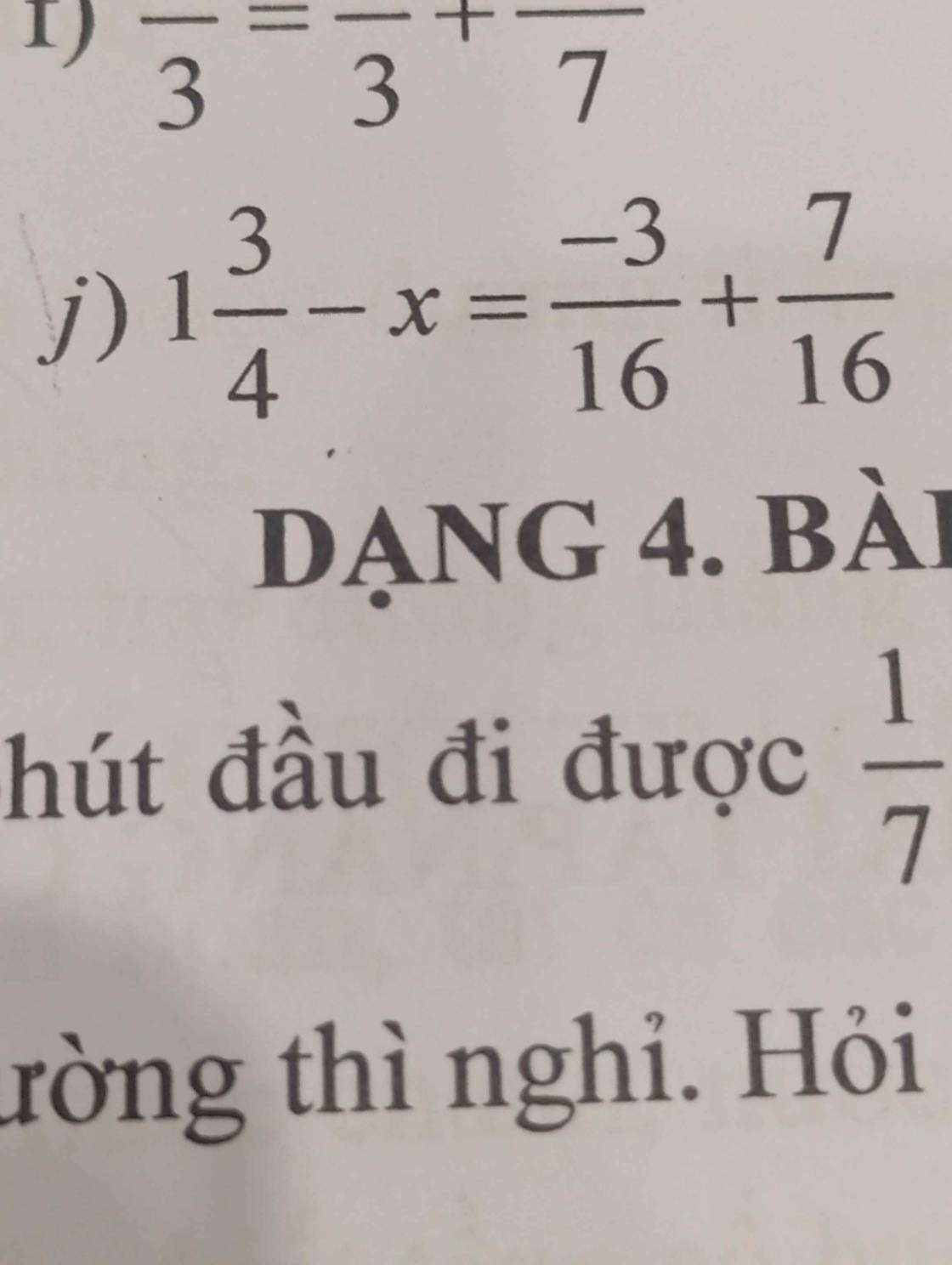
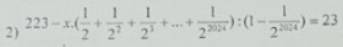
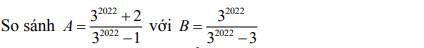
Yêu cầu đề là gì vậy bạn?