12/18

8/18

7/18

\(MSC=18\Rightarrow18:3=6;18:9=2\) 

\(\dfrac{2}{3}=\dfrac{2\times6}{3\times6}=\dfrac{12}{18}\)

\(\dfrac{4}{9}=\dfrac{4\times2}{9\times2}=\dfrac{8}{18}\)

\(\dfrac{7}{18}\) Giữ nguyên phân số

\(#NqHahh\)

\(90-5\times\left(2\times x-3\right)=45\)

        \(5\times\left(2\times x-3\right)=90-45\)

        \(5\times \left(2\times x-3\right)=45\)

                \(2\times x-3=45:5\)

                \(2\times x-3=9\)

                \(2\times x\)       \(=9+3\)

                \(2\times x\)       \(=12\)

                      \(x\)       \(=12:2\)

                      \(x\)       \(=6\)

Vậy \(x=6\)

\(90-5\times\left(2\times x-3\right)=45\\ 5\times\left(2\times x-3\right)=90-45\\ 5\times\left(2\times x-3\right)=45\\ 2\times x-3=45:5\\ 2\times x-3=9\\ 2\times x=9+3\\ 2\times x=12\\ x=12:2\\ x=6\)

MD=3cm

mà MD=MC(M là trung điểm của CD)

nên MC=3(cm)

MC=3CE

=>\(CE=\dfrac{3}{3}=1\left(cm\right)\)

=>ME=3-1=2(cm)

DE=EM+MD=2+3=5(cm)

\(\dfrac{3}{5}\times\dfrac{4}{3}+\dfrac{4}{3}-\dfrac{3}{5}\times\dfrac{4}{3}\\ =\left(\dfrac{3}{5}\times\dfrac{4}{3}-\dfrac{3}{5}\times\dfrac{4}{3}\right)+\dfrac{4}{3}\\ =0+\dfrac{4}{3}=\dfrac{4}{3}\)

\(B=\dfrac{3}{5}.\dfrac{4}{3}+\dfrac{4}{3}-\dfrac{3}{5}.\dfrac{4}{3}=\dfrac{4}{3}\)

\(x^2+5y^2< 4xy+2y\\ \Rightarrow\left(x^2-4xy+4y^2\right)+\left(y^2-2y+1\right)< 1\\ \Rightarrow\left(x-2y\right)^2+\left(y-1\right)^2< 1\) (1)

Vì x; y đều là các số nguyên

nên x-2y và y-1 cũng là các số nguyên (2)

Lại có: \(\left(x-2y\right)^2\ge0,\left(y-1\right)^2\ge0\Rightarrow\left(x-2y\right)^2+\left(y-1\right)^2\ge0\forall x,y\inℤ\) (3)

Từ (1) và (2) và (3) \(\Rightarrow0\le\left(x-2y\right)^2+\left(y-1\right)^2< 1\) và x-2y, y-1 là các số nguyên

Do đó: \(\left(x-2y\right)^2=\left(y-1\right)^2=0\\ \Rightarrow\left\{{}\begin{matrix}x-2y=0\\y-1=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=2.1=2\\y=1\end{matrix}\right.\left(nhận\right)\)

Hoặc bạn biện luận theo cách sau:

\(\left(x-2y\right)^2+\left(y-1\right)^2< 1\) (1)

Nhận thấy: \(\left(x-2y\right)^2\ge0,\left(y-1\right)^2\ge0\forall x,y\inℤ\) (2)

(1);(2) \(\Rightarrow0\le\left(x-2y\right)^2,\left(y-1\right)^2< 1\)

\(\Rightarrow-1< x-2y,y-1< 1\)

Mà: x-2y và y-1 đều là các số nguyên

Do đó nên: x-2y=y-1=0

Olm chào em, cảm ơn em đã phản hồi đến  Olm. Vấn đề em hỏi Olm xin giải đáp như sau:

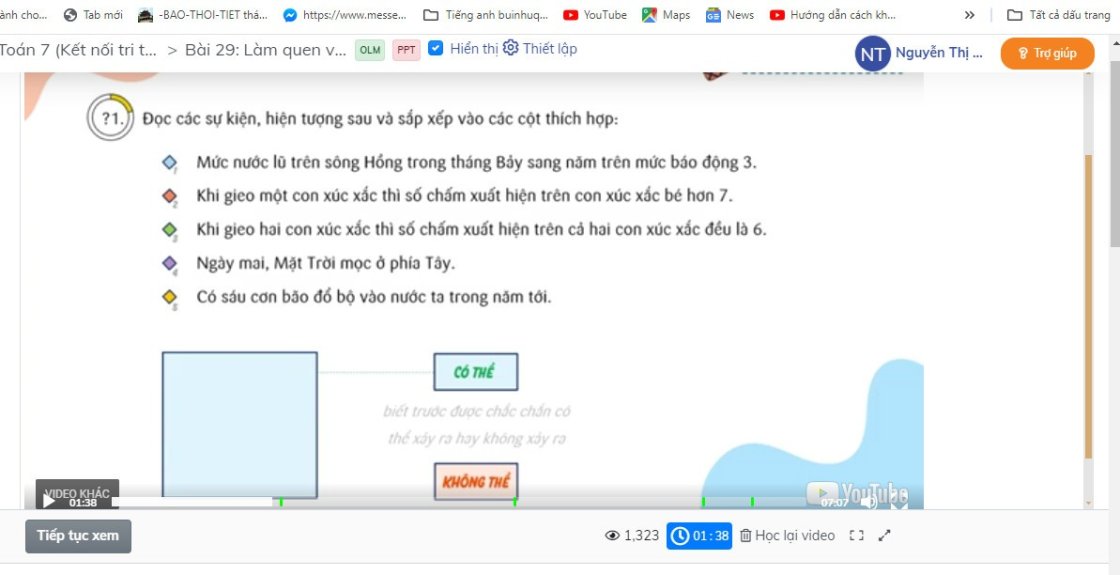
Em khẳng định mặt trời mọc ở đằng đông, đây cũng là chân lí, là thực tế không thể thay đổi trong bất cứ thời đại nào. Nên  việc ngày mai ,mặt trời mọc ở đằng  tây là không thể xảy ra.

Vậy biến cố: Ngày mai, mặt trời mọc ở đằng tây là biến cố không thể em nhé!

Sài rồi mặt trời ở phía tây

Bạn ơi đề thiếu hình vẽ nhé.

Đề không rõ ràng. Bạn xem lại đề nhé.

Bài 1:

Thay $3=x^2+xy+y^2$ vào PT(2) thì:

$2x^3=(x+y)(x^2+xy+y^2-2xy)$

$\Leftrightarrow 2x^3=(x+y)(x^2-xy+y^2)=x^3+y^3$

$\Leftrightarrow x^3=y^3\Leftrightarrow x=y$. 

Thay vào PT(1) thì: $3x^2=3\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1$

$\Rightarrow y=\pm 1$ (tương ứng)

Vậy HPT có nghiệm $(x,y)=(\pm 1, \pm 1)$

Bài 2:

Thay $2=xy(x+y)$ vào PT(2) thì:

$x^3+y^3+3xy(x+y)=8y^3$

$\Leftrightarrow (x+y)^3=(2y)^3$

$\Leftrightarrow x+y=2y\Leftrightarrow x=y$. 

Thay vào PT(1): $x^2.2x=2$

$\Leftrightarrow 2x^3=2\Leftrightarrow x^3=1\Leftrightarrow x=1$.

$\Rightarrow y=x=1$

Vậy HPT có nghiệm $(x,y)=(1,1)$