a) A nguyên khi (12n + 17) ⋮ (3n + 1)

Ta có:

12n + 17 = 12n + 4 + 13

= 4(3n + 1) + 13

Để (12n + 17) ⋮ (3n + 1) thì 13 ⋮ (3n + 1)

⇒ 3n + 1 ∈ Ư(13) = {-13; -1; 1; 13}

⇒ 3n ∈ {-14; -2, 0; 12}

⇒ n ∈ {-14/3; -2/3; 0; 4}

Mà n là số nguyên

⇒ n ∈ {0; 4}

b) Để A là số nguyên thì ⋮ (10n + 9) (5n - 1)

Ta có:

10n + 9 = 10n - 2 + 11

= 2(5n - 1) + 11

Để (10n + 9) ⋮ (5n - 1) thì 11 ⋮ (5n - 1)

⇒ 5n - 1 ∈ Ư(11) = {-11; -1; 1; 11}

⇒ 5n ∈ {-10; 0; 2; 12}

⇒ n ∈ {-2; 0; 2/5; 12/5}

Mà n là số nguyên

⇒ n ∈ {-2; 0}

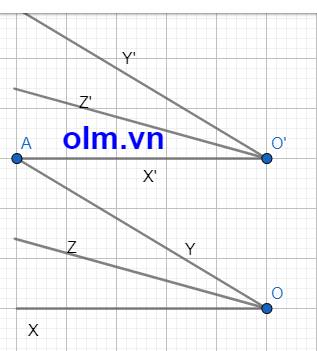
a,Kéo dài OY cắt O'X' tại A ta có: 

  \(\widehat{XOY}\) =  \(\widehat{XOA}\)  = \(\widehat{OAO'}\) (so le trong) (1)

   \(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)

Kết hợp (1) Và (2) ta có:

    \(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)

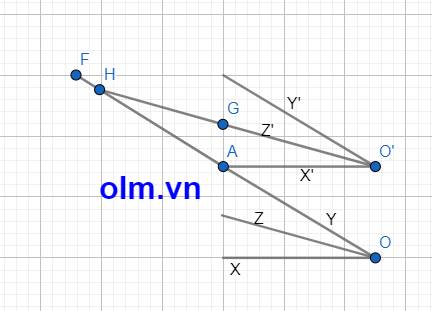
b, Kéo dài OY cắt O'Z' tại H 

             \(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY

             \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')

         Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)

               \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\)  ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)

          ⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)

         ⇒ OZ // O'Z' (đpcm)

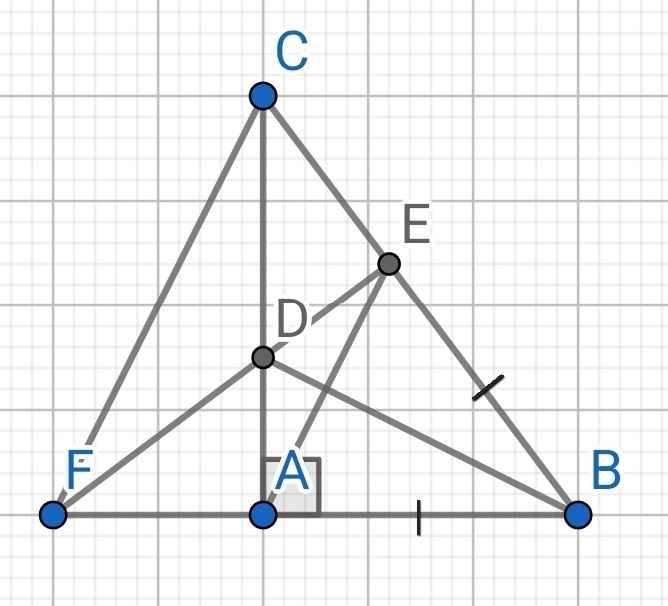 a) Xét ∆ABD và ∆EBD có:

AB = BE (gt)

∠ABD = ∠EBD (BD là tia phân giác của ABC)

BD là cạnh chung

⇒ ∆ABD = ∆EBD (c-g-c)

b) Do ∆ABD = ∆EBD (cmt)

⇒ AD = ED (hai cạnh tương ứng)

Lại do ∆ABD = ∆EBD (cmt)

⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)

⇒ ∠DAF = ∠DEC = 90⁰

Xét hai tam giác vuông: ∆DAF và ∆DEC có:

AD = ED (cmt)

∠ADF = ∠EDC (đối đỉnh)

⇒ ∆DAF = ∆DEC (cạnh góc vuông - góc nhọn kề)

⇒ AF = EC (hai cạnh tương ứng)

c) ∆BAE có:

AB = BE (gt)

⇒ ∆BAE cân tại B

⇒ ∠BEA = ∠BAE = (180⁰ - ∠ABC) : 2  (1)

Do AF = EC (cmt)

AB = BE (gt)

⇒ AF + AB = EC + BE

⇒ BF = BC

⇒ ∆BFC cân tại B

⇒ ∠BCF = ∠BFC = (180⁰ - ∠ABC) : 2  (2)

Từ (1) và (2) suy ra:

∠BEA = ∠BCF

Mà ∠BEA và ∠BCF là hai góc đồng vị

⇒ AE // CF

A = 1/4 + 1/4² + 1/4³ + ... + 1/4⁹⁹

⇒ 4A = 1 + 1/4 + 1/4² + ... + 1/4⁹⁸

⇒ 3A = 4A - A

= (1 + 1/4 + 1/4² + ... + 1/4⁹⁸) - (1/4 + 1/4² + 1/4³ + ... + 1/4⁹⁹)

= 1 - 1/4⁹⁹

⇒ A = (1 - 1/4⁹⁹)/3

Do 1 - 1/4⁹⁹ < 1

⇒ (1 - 1/4⁹⁹)/3 < 1/3

Vậy A < 1/3

Vì Ot là tia phân giác \(\widehat{mOn}\) 

nên \(\widehat{mOt}=\widehat{nOt}=\dfrac12\widehat{mOn}\)

\(\Rightarrow \widehat{mOt}=\dfrac12\cdot90^o=45^o\)

Vậy: ...

Lời giải:

Do $(2023-x)^2\geq 0$ với mọi $x$ nên:

$3(y-3)^2=16-(2023-x)^2\leq 16<18$

$\Rightarrow (y-3)^2< 6$

Mà $(y-3)^2\geq 0$ và $(y-3)^2$ là số chính phương với mọi $y$ nguyên.

$\Rightarrow (y-3)^2=0$ hoặc $(y-3)^2=4$

Nếu $(y-3)^2=0$ thì $y=3$.

Khi đó: $(2023-x)^2=16-3.0^2=16$

$\Rightarrow 2023-x=4$ hoặc $2023-x=-4$

$\Rightarrow x=2019$ hoặc $x=2027$

Nếu $(y-3)^2=4\Rightarrow y-3=2$ hoặc $y-3=-2$

$\Rightarrow y=5$ hoặc $y=1$
Khi đó:

$(2023-x)^2=16-3.4=4=2^2=(-2)^2$
$\Rightarrow 2023-x=2$ hoặc $2023-x=-2$

$\Rightarrow x=2021$ hoặc $x=2025$

5\(x\) - 9 = 5 + 3\(x\)

5\(x\) - 3\(x\) = 5 + 9

2\(x\)       = 14

  \(x\)      =  14 : 2

   \(x\)     = 7 

Gọi biểu thức trên là A

Ta có:

2A = (\(\dfrac{1}{2.4}\)+\(\dfrac{1}{4.6}\)+...+\(\dfrac{1}{x.\left(x+2\right)}\)).2

2A = \(\dfrac{2}{2.4}\)+\(\dfrac{2}{4.6}\)+...+\(\dfrac{2}{x\left(x+2\right)}\)

2A = \(\dfrac{1}{2}\)-\(\dfrac{1}{4}\)+\(\dfrac{1}{4}\)-\(\dfrac{1}{6}\)+...+\(\dfrac{1}{x}\)-\(\dfrac{1}{x+2}\)

2A = \(\dfrac{1}{2}\)-\(\dfrac{1}{x+2}\)

mà A = \(\dfrac{1}{10}\)(đề bài)

nên 2A = \(\dfrac{2}{10}\) hay \(\dfrac{1}{2}\) - \(\dfrac{1}{x+2}\) = \(\dfrac{2}{10}\)

                     suy ra \(\dfrac{1}{x+2}\) = \(\dfrac{1}{2}\)-\(\dfrac{2}{10}\)=\(\dfrac{3}{10}\) 

Không bạn nhé. Đây là phân thức.

\(\left(-5\right)^{18}:5^{x-3}=25^6\)

\(=>5^{x-3}=\left(-5\right)^{18}:25^6\)

\(=>5^{x-3}=5^{18}:5^{12}\)

\(=>5^{x-3}=5^6\)

\(=>x-3=6\)

\(=>x=6+3\)

\(=>x=9\)

\((-5)^{18}:5^{x-3}=25^6\\\Rightarrow 5^{18}:5^{x-3}=(5^2)^6\\\Rightarrow 5^{18-(x-3)}=5^{2\cdot6}\\\Rightarrow 5^{18-x+3}=5^{12}\\\Rightarrow 5^{21-x}=5^{12}\\\Rightarrow 21-x=12\\\Rightarrow x=21-12\\\Rightarrow x=9\\\mathit{Vậy}:x=9\)