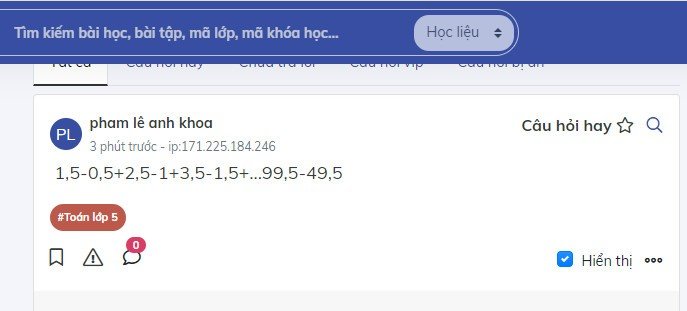
1,5-0,5+2,5-1+3,5-1,5+...99,5-49,5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(A=8abc+4\left(ab+bc+ca\right)+2\left(a+b+c\right)+1\\= 8abc+4ab+4bc+4ca+2a+2b+2c+1\\ =\left(8abc+4ab\right)+\left(4bc+2b\right)+\left(4ca+2a\right)+\left(2c+1\right)\\ =4ab\left(2c+1\right)+2b\left(2c+1\right)+2a\left(2c+1\right)+\left(2c+1\right)\\ =\left(2c+1\right)\left(4ab+2b+2a+1\right)\\ =\left(2c+1\right)\left[\left(4ab+2b\right)+\left(2a+1\right)\right]\\ =\left(2c+1\right)\left[2b\left(2a+1\right)+\left(2a+1\right)\right]\\ =\left(2c+1\right)\left(2a+1\right)\left(2b+1\right)\)

a, A''Có đúng 2 nữ''
\(C^2_3.C_{56}^2\)
\(P\left(A\right)=\dfrac{C_3^2.C_{56}^2}{C_{59}^4}\)
b, B''Có ít nhất 2 nam''
TH1 : Có 2 nam \(C_{56}^2.C_3^2\)
TH2 : Có 3 nam \(C_{56}^3.C_3^1\)
TH3 : Có 4 nam \(C^4_{56}\)
\(\Rightarrow C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4\)
\(P\left(B\right)=\dfrac{C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4}{C_{59}^4}\)
c, C''Có nhiều nhất 2 nam''
TH1 : Có 1 nam \(C_{56}^1.C_3^3\)
TH2 : Có 2 nam \(C_{56}^2.C_3^2\)
\(\Rightarrow C_{56}^2.C_3^3+C_{56}^2.C_3^2\)
\(P\left(C\right)=\dfrac{C_{56}^2.C_3^3+C^2_{56}.C_3^2}{C_{59}^4}\)

Bạn ấn vào tên của người muốn kết bạn:
Bạn bấm vào nút Kết Bạn để gửi lời mời kết bạn nhé!

\(A=abc-\left(ab+bc+ca\right)+a+b+c-1\\ =abc-ab-bc-ca+a+b+c-1\\ =\left(abc-ab\right)+\left(-bc+b\right)+\left(-ca+a\right)+\left(c-a\right)\\ =ab\left(c-1\right)-b\left(c-1\right)-a\left(c-1\right)+\left(c-1\right)\\ =\left(ab-b-a+1\right)\left(c-1\right)\\ =\left[b\left(a-1\right)-\left(a-1\right)\right]\left(c-1\right)\\ =\left(a-1\right)\left(b-1\right)\left(c-1\right)\)
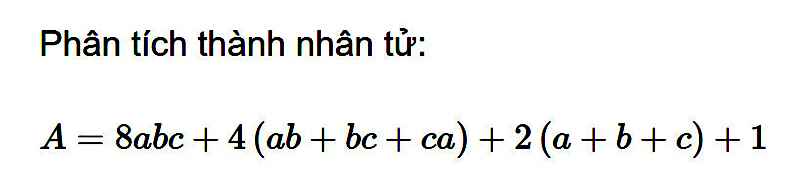
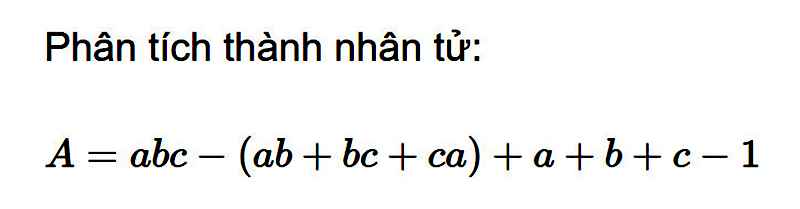
\(1,5-0,5+2,5-1+3,5-1,5+...+99,5-49,5\)
\(=1+1,5+2+...+50\)
Quy luật : Số đằng sau cách số đằng trước \(0,5\) đơn vị.
`= >` Số số hạng dãy trên là:
\(\left(50-1\right):0,5+1=99\) (số hạng)
Tổng trên là:
\(\left(50+1\right)\times99:2=2524,5\)
Đáp số : 2524,5
chỗ .... 99,5 là dấu cộng hay dấu trừ vậy em???