mn giúp mình bài 7 với ạ!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình tự vẽ nhé
Xét △OAD và △OCB, có
OA=OC (giả thiết)
Góc AOD chung
OD=OB(giả thiết)
=> △OAD=△OCB (cgc)
b) vì △OAD=△OCB
=> AD=BC
lại có: AB = OB-OA
CD = OD-OC
=> AB=CD
Xét △CAB và △ACD, có
AC cạnh chung
AB=CD
AD=CB
=> △CAB=△ACD
cho tam giác ABC có góc A=80 độ.dựng AH vuông góc với BC(H thuộc BC).Trên ttia đối của tia HA lấy điểm D sao cho HD=HA. câu a, chứng minh AC=DC câu b, chứng minh tam giác ABC= tam giác DBC câu c, TÍNH SỐ ĐO GÓC bdc



Ta có \(111...11+444...44+1\)
100cs 50cs
\(=\dfrac{1}{9}.999...99+\dfrac{4}{9}.999...99+1\)
100cs 50cs
\(=\dfrac{10^{100}-1}{9}+\dfrac{4\left(10^{50}-1\right)}{9}+1\)
\(=\dfrac{10^{100}-1+4.10^{50}-4+9}{9}\)
\(=\dfrac{10^{100}+4.10^{50}+4}{9}\)
\(=\left(\dfrac{10^{50}+2}{3}\right)^2\)
Vì \(10^{50}+2\) có tổng các chữ số là 3 nên \(\dfrac{10^{50}+2}{3}\inℕ\). Vậy ta có đpcm.

a) \(\left|x\right|=3,5\)
\(\Rightarrow\left[{}\begin{matrix}x=3,5\\x=-3,5\end{matrix}\right.\)
b) \(\left|1-x\right|+0,73=3\)
\(\Rightarrow\left|1-x\right|=3-0,73\)
\(\Rightarrow\left|1-x\right|=2,27\)
\(\Rightarrow\left[{}\begin{matrix}1-x=2,27\\1-x=-2,27\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1,27\\x=3,27\end{matrix}\right.\)
c) \(\dfrac{-5}{8}+x=\dfrac{4}{9}\)
\(\Rightarrow x=\dfrac{4}{9}-\left(\dfrac{-5}{8}\right)\)
\(\Rightarrow x=\dfrac{77}{72}\)

\(\dfrac{3x-9}{x+9}=\dfrac{4}{5}\)
\(\Rightarrow4\left(x+9\right)=5\left(3x-9\right)\)
\(\Rightarrow4x+36=15x-45\)
\(\Rightarrow15x-4x=36+45\)
\(\Rightarrow11x=81\)
\(\Rightarrow x=\dfrac{81}{11}\)

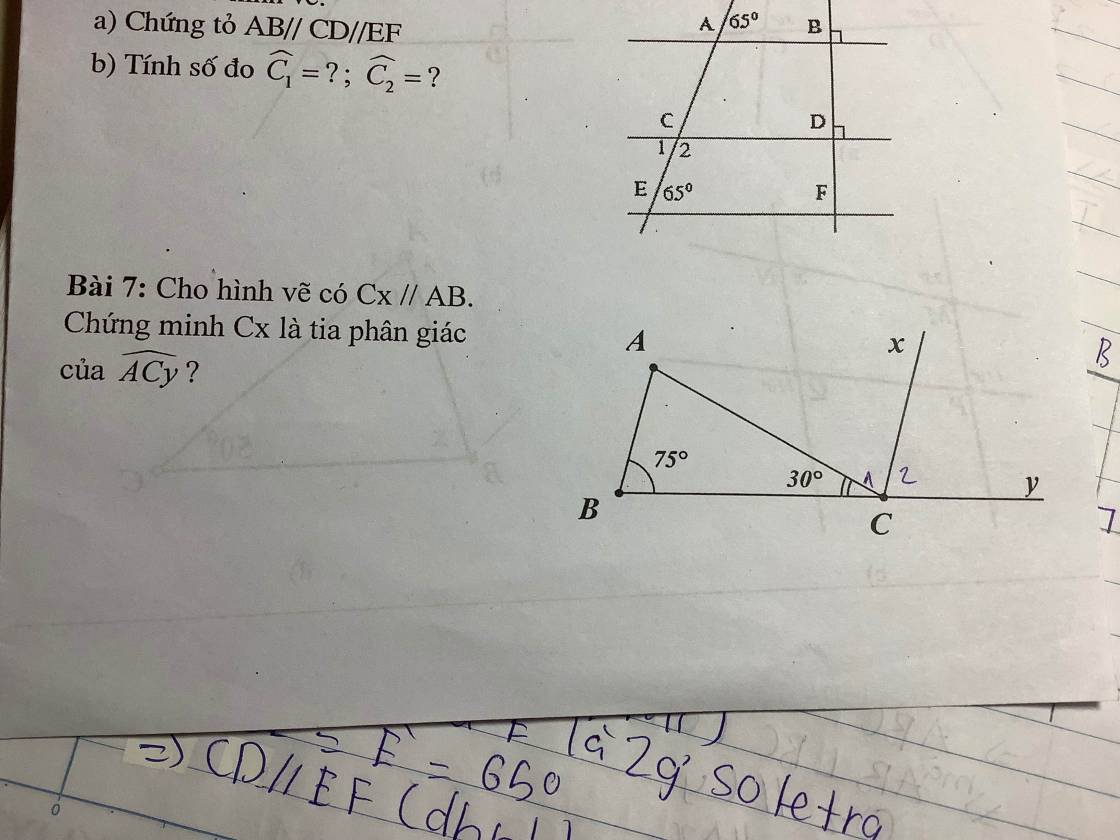
Bài 7:
Vì $Cx\parallel AB$ nên:
$\widehat{C_1}=\widehat{BAC}$ (2 góc so le trong)
$=180^0-\widehat{ABC}-\widehat{ACB}=180^0-75^0-30^0=75^0$
$\widehat{C_2}=180^0-\widehat{ACB}-\widehat{C_1}$
$=180^0-30^0-75^0=75^0$
$\Rightarrow \widehat{C_1}=\widehat{C_2}$
$\Rightarrow Cx$ là tia phân giác của $\widehat{ACy}$
Bài 6:
a. Ta thấy $AB\perp BD, CD\perp BD\Rightarrow AB\parallel CD(1)$
$CD\perp DF, EF\perp DF\Rightarrow CD\parallel EF(2)$
Từ $(1); (2)\Rightarrow AB\parallel CD\parallel EF$
b.
Vì $CD\parallel EF$ nên:
$\widehat{C_1}=\widehat{CEF}=65^0$ (2 góc so le trong)
$\widehat{C_2}=180^0-\widehat{C_1}=180^0-65^0=115^0$