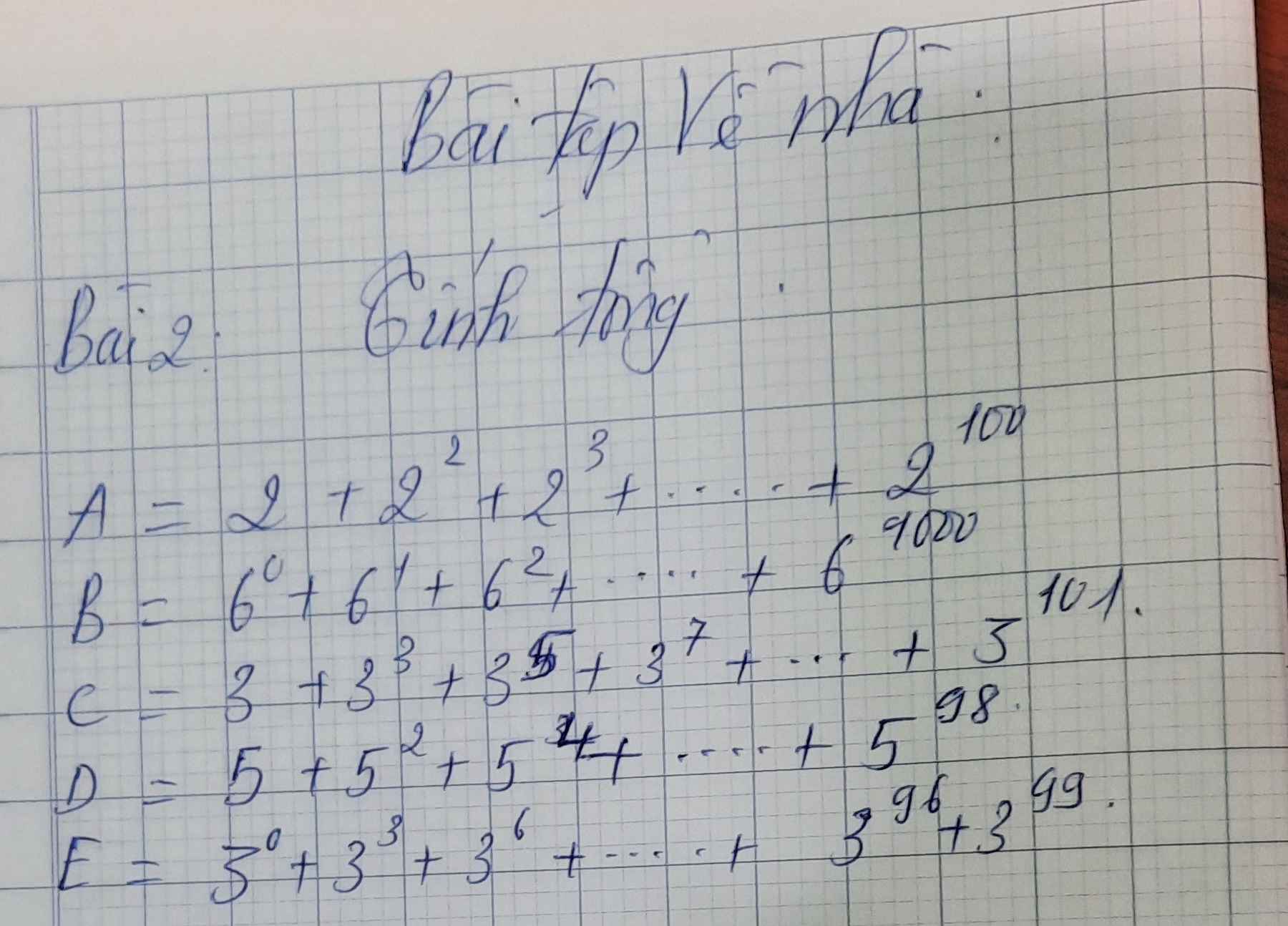\(A=2+2^2+...+2^{100}\\ 2A=2^2+2^3+...+2^{101}\\ 2A-A=\left(2^2+2^3+...+2^{101}\right)-\left(2+2^2+...+2^{100}\right)\\ A=2^{101}-2\\ B=6^0+6^1+6^2+...+6^{1000}\\ 6B=6+6^2+...+6^{1001}\\ 6B-B=\left(6+6^2+...+6^{1001}\right)-\left(1+6+...+6^{1000}\right)\\ 5B=6^{1001}-1\\ B=\dfrac{6^{1001}-1}{5}\\ C=3+3^3+3^5+...+3^{101}\\ 3^2C=3^3+3^5+3^7+...+3^{103}\\ 9C-C=\left(3^3+3^5+3^7+...+3^{103}\right)-\left(3+3^3+3^5+...+3^{101}\right)\\ 8C=3^{103}-3\\ C=\dfrac{3^{103}-3}{8}\)

\(D=5+5^2+5^4+...+5^{98}\\ 5^2D=5^3+5^4+5^6+...+5^{100}\\ 25D-D=\left(5^3+5^4+5^6+....+5^{100}\right)-\left(5+5^2+5^4+...+5^{98}\right)\\ 24D=5^{100}+5^3-5-5^2\\ 24D=5^{100}+125-5-25\\ 24D=5^{100}+95\\ D=\dfrac{5^{100}+95}{24}\\ E=3^0+3^3+3^6+...+3^{96}+3^{99}\\ E=1+3^3+...+3^{99}\\ 3^3E=3^3+3^6+...+3^{102}\\ 27E-E=\left(3^3+3^6+...+3^{102}\right)-\left(1+3^3+...+3^{99}\right)\\ 26E=3^{102}-1\\ E=\dfrac{3^{102}-1}{6}\)

Gọi `x` là số thuộc ước của 300 và bội của 25

`=> x ⋮ 25` và `300 ⋮ x`

Ta có: 

`300 = 1. 2^2 . 3 . 5^2`

Mà ` x ⋮ 25` nên `x` có dạng: `5^2 k` (`k ∈ N`*)

`=> k ∈ ` {`1 ; 2 ; 2^2 ; 3 ; 2 . 3 ; 2^2 . 3`}

`=> k ∈` {`1 ; 2 ; 4 ; 3 ; 6; 12`}

Khi đó `x ∈ {25;50;100;75;150;300}`

Ư(300) = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 200, 300}

B(25)    = {1, 25, 50, 75, 100, 125, 150, 175, 200, 225, 250, 275, 300}

Vậy, các số vừa thuộc về Ư(300) vừa thuộc về B(25) là:

    {25, 50, 75, 100, 150}

\(\left(x+1\right)^3+9=-116\)

=>\(\left(x+1\right)^3=-116-9=-125=\left(-5\right)^3\)

=>x+1=-5

=>x=-5-1=-6

= 1 ; 5 ; 25 ;  -1 ; -5 ; -25

nhé bạn

sorry bạn dấu = phải thay = dấu ϵ

Gọi số bi của Nam là x(viên)

(ĐIều kiện: \(x\in Z^+\))

Số viên bi của Dũng là x-7(viên)

Số viên bi của Thanh là x+5(viên)

Tổng số viên bi là 94 viên nên ta có:

x+x-7+x+5=94

=>3x=96

=>x=32(nhận)

Vậy: Số bi của Nam là 32 viên

Số viên bi của Dũng là 32-7=25 viên

Số viên bi của Thanh là 32+5=37 viên

a: Hiệu vận tốc hai xe là 60-40=20(km/h)

Hai xe gặp nhau sau 40:20=2(giờ)

Hai xe gặp nhau lúc 12h+2h=14h

b: Khi gặp nhau thì nơi gặp cách A:

2x40=80(km)

Diện tích xung quanh là:

\(\left(7+4\right)\cdot2\cdot5=10\cdot11=110\left(m^2\right)\)

Diện tích trần nhà là \(7\cdot4=28\left(m^2\right)\)

Diện tích cần quét vôi là \(110+28-7,6=110+20,6=130,6\left(m^2\right)\)

Số tiền cần phải trả là:

\(130,6\cdot1700=222020\left(đồng\right)\)

\(C=5\dfrac{9}{10}:\dfrac{3}{2}-\left(2\dfrac{1}{3}\cdot4\dfrac{1}{2}-2\cdot2\dfrac{1}{3}\right):\dfrac{7}{4}\)

\(=\dfrac{59}{10}\cdot\dfrac{2}{3}-\left(\dfrac{7}{3}\cdot\dfrac{9}{2}-2\cdot\dfrac{7}{3}\right)\cdot\dfrac{4}{7}\)

\(=\dfrac{59}{15}-\dfrac{7}{3}\cdot\dfrac{5}{2}\cdot\dfrac{4}{7}\)

\(=\dfrac{59}{15}-\dfrac{10}{3}=\dfrac{9}{15}=\dfrac{3}{5}\)

\(42\cdot40+6\cdot8\cdot21-22\cdot96\)

\(=42\cdot40+24\cdot42-22\cdot96\)

\(=42\left(40+24\right)-22\cdot1,5\cdot64\)

\(=64\cdot42-64\cdot33=64\cdot9=576\)

\(250=5^3\cdot2\)

=>\(Ư\left(250\right)=\left\{1;-1;2;-2;5;-5;10;-10;25;-25;50;-50;125;-125;250;-250\right\}\)

\(Ư\left(250\right)\)\(=\left\{1;2;5;10;25;50;125;250\right\}\)