Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`180 = 2.2. 3.3 . 5`
`2024 = 2.2.2 . 11 . 23`
`1500 = 2.2.3.5.5.5`
`400 = 2.2.2.2.5.5`
`504 = 2.2.2.3.3.7`
`890 = 2.5.89`

d: \(\left|-5-\sqrt{2}\right|=5+\sqrt{2}\)
c: \(\left|4+\sqrt{3}\right|=4+\sqrt{3}\)
d: \(\left|-\dfrac{4}{15}\right|=\dfrac{4}{15}\)
a: \(\left|3,02\right|=3,02\)


a: Các số tự nhiên chia hết cho 2 trong khoảng từ 1 đến 100 là: 2;4;6;...;100
Số số tự nhiên chia hết cho 2 trong khoảng từ 1 đến 100 là: \(\dfrac{100-2}{2}+1=50\left(số\right)\)
Các số tự nhiên chia hết cho 5 trong khoảng từ 1 đến 100 là: 5;10;...;100
Số số tự nhiên chia hết cho 5 trong khoảng từ 1 đến 100 là:
\(\dfrac{100-5}{5}+1=\dfrac{95}{5}+1=20\left(số\right)\)
b: Các số có 3 chữ số chia hết cho 3 là 102;105;...;999
Số số tự nhiên có 3 chữ số chia hết cho 3 là:
\(\dfrac{999-102}{3}+1=\dfrac{897}{3}+1=\dfrac{900}{3}=300\left(số\right)\)

a: \(\sqrt{50}>\sqrt{49}\)
mà \(\sqrt{49}=7\)
nên \(\sqrt{50}>7\)
b: \(\sqrt{27}>\sqrt{25}=5\)
=>\(\dfrac{4}{\sqrt{27}}< \dfrac{4}{5}\)
c: \(\dfrac{3}{\sqrt{7}}>1;\dfrac{\sqrt{7}}{3}< 1\)
Do đó: \(\dfrac{3}{\sqrt{7}}>\dfrac{\sqrt{7}}{3}\)

Bài 2:
a:
\(-4,4\left(9\right)-5,8\left(1\right)\simeq-4,5-5,8=-10,3\)
\(-4,4\left(9\right)-5,8\left(1\right)\)
\(=-\dfrac{9}{2}-\dfrac{-523}{90}=-\dfrac{9}{2}+\dfrac{523}{90}=\dfrac{118}{90}=\dfrac{59}{45}\)
b:
\(-12,\left(7\right)\cdot3,\left(12\right)\simeq-12,8\cdot3,1\simeq-40\)
\(-12,\left(7\right)\cdot3,\left(12\right)\)
\(=-\dfrac{115}{9}\cdot\dfrac{103}{33}=\dfrac{11845}{297}\)
c: \(9,\left(49\right):\left[-5,\left(09\right)\right]\simeq9,5:\left(-5,1\right)\simeq-1,9\)
\(9,\left(49\right):\left[-5,\left(09\right)\right]\)
\(=\dfrac{940}{99}:\dfrac{-56}{11}=\dfrac{940}{99}\cdot\dfrac{11}{-56}\)
\(=\dfrac{940}{-56}\cdot\dfrac{1}{9}=-\dfrac{235}{14\cdot9}=-\dfrac{235}{126}\)
Bài 1:
a: \(9,4\simeq9\)
b: \(3,51\simeq4\)
c: \(-7,505\simeq-8\)
d: \(-1.199\simeq-1\)

\(144=2^4\cdot3^2;192=2^6\cdot3\)
=>\(ƯCLN\left(144;192\right)=2^4\cdot3=48\)
=>\(ƯC\left(144;192\right)=Ư\left(48\right)=\left\{1;2;3;4;6;8;12;16;24;48\right\}\)
=>Các ước chung lớn hơn 20 của 144 và 192 là 24;48

\(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)
=>(a+b)(c-a)=(a-b)(c+a)
=>\(ac-a^2+bc-ba=ac+a^2-bc-ab\)
=>\(-a^2+bc=a^2-bc\)
=>\(-2a^2=-2bc\)
=>\(a^2=bc\)
\[
\frac{a+b}{a-b} = \frac{c+a}{c-a}
\]
Ta sẽ thực hiện phép nhân chéo:
\[
(a+b)(c-a) = (a-b)(c+a)
\]
Khai triển hai vế của phương trình:
- Vế trái:
\[
(a+b)(c-a) = ac - a^2 + bc - ab
\]
- Vế phải:
\[
(a-b)(c+a) = ac + a^2 - bc - ab
\]
Từ đó ta có:
\[
ac - a^2 + bc - ab = ac + a^2 - bc - ab
\]
Giản lược hai vế:
\[
-a^2 + bc = a^2 - bc
\]
Chuyển các hạng tử về cùng một vế:
\[
-a^2 + bc - a^2 + bc = 0
\]
\[
-2a^2 + 2bc = 0
\]
Chia cả hai vế cho 2:
\[
-a^2 + bc = 0
\]
Chuyển \(-a^2\) qua vế phải:
\[
bc = a^2
\]

Do thương của phép chia là 2 nên số bị chia gấp số chia 5 lần
Ta có sơ đồ:
Số bị chia: 5 phần
Số chia: 1 phần
Tổng số phần bằng nhau là:
`5+1=6` (phần)
Giá trị 1 phần là:
`288 : 6 = 48`
Số bị chia là:
`48` x `5 = 240`
Số chia là:
`240 : 5 = 48`
Đáp số: ...
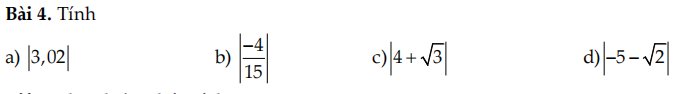
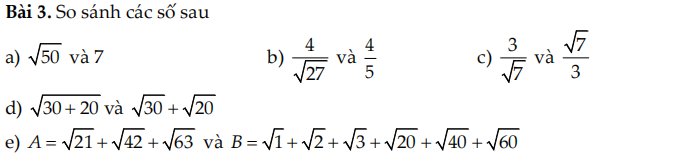

a: \(\left|-\dfrac{1}{3}\right|-\left(-\dfrac{6}{7}\right)^0+\left(\dfrac{1}{2}\right)^2:2\)
\(=\dfrac{1}{3}-1+\dfrac{1}{4}:2=-\dfrac{2}{3}+\dfrac{1}{8}=\dfrac{-16}{24}+\dfrac{3}{24}=-\dfrac{13}{24}\)
b: \(\left(\dfrac{2}{3}\right)^3+\sqrt{\dfrac{49}{81}}-\left|-\dfrac{7}{3}\right|:3\)
\(=\dfrac{8}{27}+\dfrac{7}{9}-\dfrac{7}{3}\cdot\dfrac{1}{3}\)
\(=\dfrac{8}{27}+\dfrac{7}{9}-\dfrac{7}{9}=\dfrac{8}{27}\)
c: \(\sqrt{\dfrac{25}{49}}+\left(5555\right)^0+\left|-\dfrac{2}{7}\right|\)
\(=\dfrac{5}{7}+1+\dfrac{2}{7}\)
=1+1=2