cho tam giác ABC vuông tại A,AB<AC.Lấy điểm D sao cho A là trung điểm của BD.a)Chứng minh CA là tia phân giác của góc BCD;b)Vẽ BM vuông góc với DC tại M,BM cắt AC tại H.Vẽ HN vuông góc với BC tại N.Chứng minh tam giác CMN cân và MN//BD;c)So sánh HB và HM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

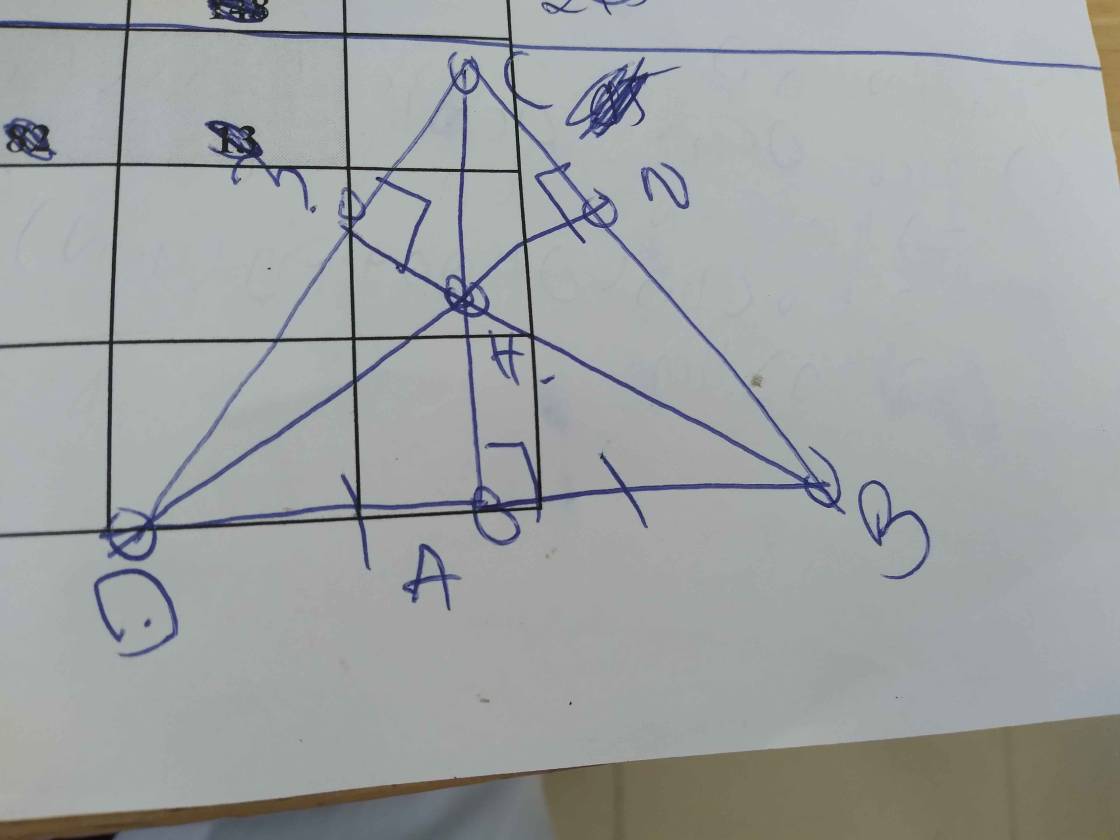



Để chứng minh rằng \( BM = CN \), chúng ta sẽ sử dụng tính chất của tam giác cân.
Vì tam giác \( ABC \) cân tại \( A \), nên ta có \( AM = MC \) và \( AN = NB \), vì \( M \) là trung điểm của \( AC \) và \( N \) là trung điểm của \( AB \).
Bây giờ, ta cần chứng minh \( BM = CN \).
Ta có thể sử dụng định lí đối xứng của tam giác để chứng minh điều này.
Xét tam giác \( AMC \) và \( ANB \):
- \( AM = MC \) (vì \( M \) là trung điểm của \( AC \))
- \( AN = NB \) (vì \( N \) là trung điểm của \( AB \))
- \( AC = AB \) (vì tam giác \( ABC \) cân tại \( A \))
Theo định lí đối xứng của tam giác, ta có \( BM = CN \), vì hai tam giác \( AMC \) và \( ANB \) là đối xứng với nhau qua đường trung tuyến \( MN \).
Do đó, \( BM = CN \).

- Em tự hào về truyền thống làng mình.
- Giới thiệu cho bạn bè về truyền thống làng mình.
- Học hỏi từ ông, cha về truyền thống.
- Tìm cách để phát triển truyền thống đó.



#include <bits/stdc++.h>
using namespace std;
int main()
{
long long n;
cin>>n;
long long tong=0;
for(int i=1; i<=n; i++)
{
tong+=i;
}
cout<<tong;
}

Câu 1:
1. D. aunt
2. C. flood
3. A. played
4. B. health
Câu 2:
1. C. arrive
2. B. power

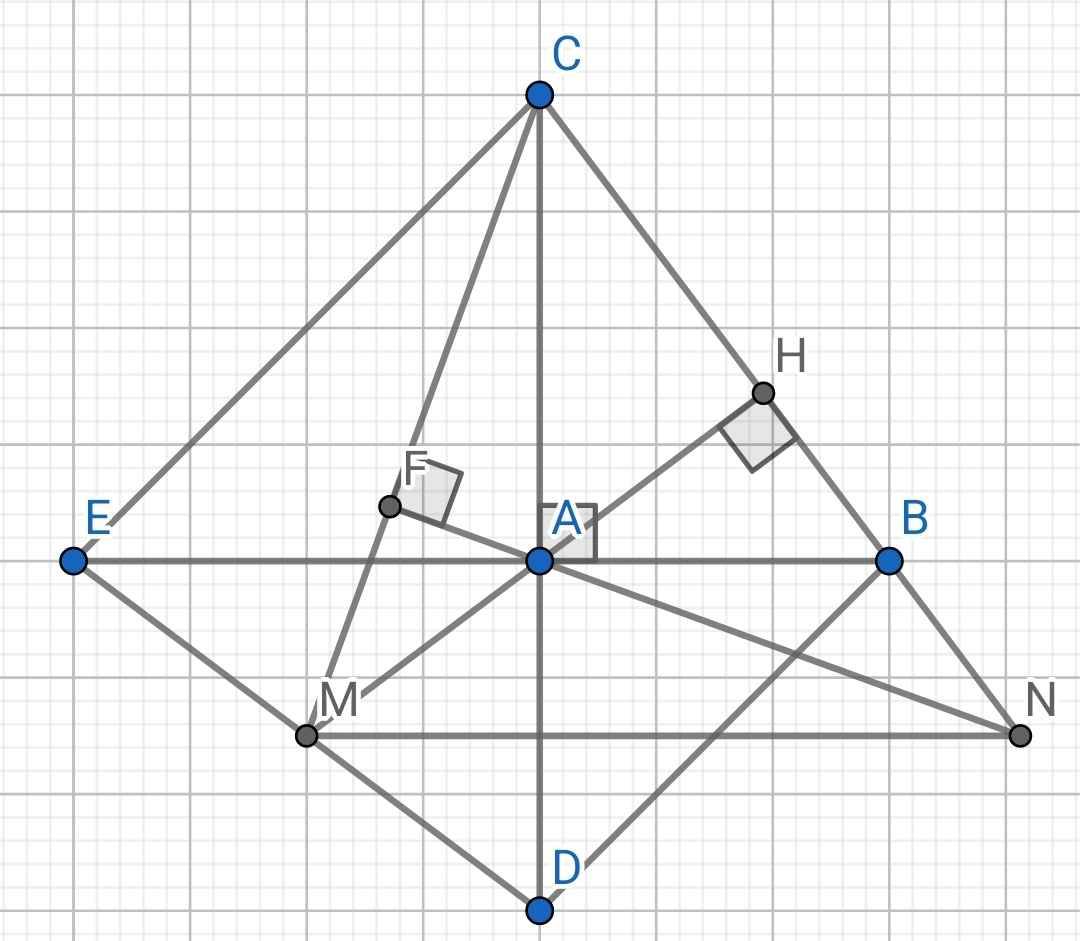
a) Do ∆ADB vuông cân tại A (gt)
⇒ AB = AD
Do ∆AEC vuông cân tại A (gt)
⇒ AE = AC
Xét hai tam giác vuông: ∆ABC và ∆ADE có:
AB = AD (cmt)
AC = AE (cmt)
∆ABC = ∆ADE (hai cạnh góc vuông)
⇒ BC = DE (hai cạnh tương ứng)
b) Do ∆ADE vuông cân tại A (gt)
⇒ ∠ADB = ∠ABD = 45⁰
Do ∆AEC vuông cân tại A (gt)
⇒ ∠ACE = ∠AEC = 45⁰
⇒ ∠ACE = ∠ADB = 45⁰
Mà ∠ACE và ∠ADB là hai góc so le trong
⇒ DB // EC
c) Do AH ⊥ BC (gt)
⇒ MH ⊥ CN
Do AF ⊥ MC (gt)
⇒ NF ⊥ MC
∆CMN có:
MH ⊥ CN (cmt)
NF ⊥ MC (cmt)
⇒ MH và NF là hai đường cao của ∆CMN
Mà MH cắt NF tại A
⇒ CA là đường cao thứ ba của ∆CMN
⇒ CA ⊥ MN
d) Em xem lại đề nhé