choΔABCvg tại A ,AB nhỏ hơn AC, đg cao AH
a,.tính BC,AH,góc B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Rightarrow\)Trong câu “cảm vì nỗi ấy”, từ “cảm” có nghĩa là cảm nhận, cảm thấy hoặc hiểu được. Đây là một trạng thái tình cảm mà người nói đang trải qua khi đối mặt với “nỗi ấy”. “Nỗi ấy” thường được dùng để chỉ một điều gì đó không được nói rõ ra nhưng người nghe có thể hiểu được qua ngữ cảnh. Trong trường hợp này, “cảm vì nỗi ấy” có thể hiểu là người nói đang cảm nhận sự thấu hiểu sâu sắc về một điều gì đó mà họ gọi là “nỗi ấy”.

Theo mình tìm hiểu là từ "há" là: từ biểu thị ý như muốn hỏi, nhưng thật ra là để khẳng định "không lẽ nào lại như thế".

Bài làm
Mỗi lần đứng trước lá cờ Tổ quốc, lòng tôi đầy xúc động. Lá cờ đỏ sao vàng, biểu tượng của quốc gia, là niềm tự hào của mỗi người dân Việt Nam. Khi ngắm nhìn lá cờ tung bay trong gió, tôi cảm nhận được sự hùng vĩ, kiên cường của dân tộc mình.
Khi tiếng Quốc ca Việt Nam vang lên, lòng tôi tràn đầy niềm tự hào và kính trọng. Những giai điệu trang nghiêm, phổ nhạc du dương của bài hát đã khắc sâu vào tâm trí tôi. Mỗi lần hát Quốc ca, tôi luôn nhớ về những hy sinh, gian khổ mà cha ông ta đã trải qua để giành lại độc lập cho Tổ quốc. Trước lá cờ Tổ quốc và tiếng Quốc ca vang lên, tôi luôn giữ thái độ nghiêm túc, tôn trọng. Tôi đứng thẳng, nhìn về phía lá cờ và hát theo từng lời của Quốc ca. Đó không chỉ là một nghi thức mà còn là biểu hiện của lòng yêu nước, lòng kính trọng Tổ quốc. Những khoảnh khắc này không chỉ làm tôi tự hào về quê hương mình mà còn thúc đẩy tôi không ngừng nỗ lực học tập và lao động để xứng đáng là công dân của Việt Nam. Tôi hiểu rằng mỗi chúng ta đều có trách nhiệm góp phần vào sự phát triển của đất nước.
Mỗi lần đứng trước lá cờ Tổ quốc và hát Quốc ca, tôi cảm thấy mình không chỉ là một cá nhân mà là một phần của cộng đồng, của dân tộc Việt Nam. Đó là niềm tự hào và trách nhiệm mà tôi mang trong tim.

Sửa lại đề 1 chút là thuận tay phải mới là trội hoàn toàn nhé.
Sơ đồ phả hệ:
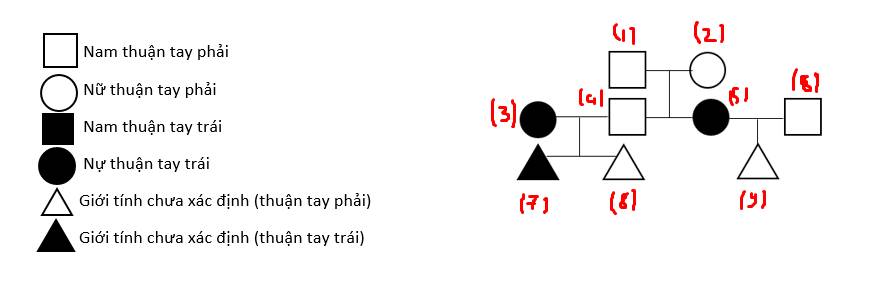
Kí hiệu alen thuận tay phải và gen thuận tay trái lần lượt là A và a. Gen nằm trên NST thường.
Cặp bố mẹ (1), (2) sinh ra người con (5) thuận tay trái (có KG aa) nên kiểu gen của (1), (2) đều phải có 1 alen lặn a. Hơn nữa, cả cặp bố mẹ (1), (2) đều thuận tay phải nên cả 2 đều phải có KG là Aa.
Thế thì người con (4) hoặc có KG AA hoặc Aa. KG của người vợ (3) chắc chắn là aa. Vì cặp vợ chồng (3), (4) sinh ra người con (7) có KG aa nên KG của người con trai (4) là Aa. Dẫn đến người con (8) phải có KG Aa.
Cặp vợ chồng (5), (6) sinh ra người con (9) thuận tay phải nên người con (9) phải có KG Aa. Trong khi người chồng (6) có thể mang KG AA hoặc Aa.

Ta có \(a^4+b^4\ge2a^2.b^2\) (Bất đẳng thức Cô si với \(a^2;b^2\ge0\) )
Tương tự \(b^4+c^4\ge2b^2.c^2;a^4+c^4\ge2a^2.c^2\)
Do đó: \(a^4+b^4+c^4\ge\dfrac{2a^2b^2+2b^2c^2+2a^2c^2}{2}=a^2b^2+b^2c^2+a^2c^2\)(1)
Ta lại có:\(a^2b^2+b^2c^2\ge2ab^2c;b^2c^2+a^2c^2\ge2abc^2;a^2c^2+a^2b^2\ge2a^2bc\)
Nên\(a^2b^2+b^2c^2+a^2c^2\ge a^2bc+ab^2c+abc^2=abc\left(a+b+c\right)=3abc\left(a+b+c=3,gt\right)\)
(1);(2) => \(a^4+b^4+c^4\ge3abc\) ;đẳng thức xảy ra khi a = b = c = 1 (*)
Giả sử: \(a^3+b^3+c^3\ge3abc\\ \Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\ge0\\ \Leftrightarrow\left(a+b+c\right)^3-3ab\left(a+b+c\right)-3c\left(a+b\right)\left(a+b+c\right)\ge0\\ \Leftrightarrow\left(a+b+c\right)\left[\left(a+b+c\right)^2-ab-bc-ac\right]\ge0\\2.3\left(a^2+b^2+c^2-ab-bc-ac\right)\ge0\\
\Leftrightarrow3\left(2a^2+2b^2+2c^2-2ab-2bc-2ac\right)\ge0\\\Leftrightarrow3\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\right]\ge0\)
Đúng mới mọi a,b,c ϵR
Vậy \(a^3+b^3+c^3\ge3abc\) và đẳng thức xảy ra khi a=b=c=(a+b+c)/3 =1(**)
Ta lại có \(a^4\ge a^3;b^4\ge b^3;c^4\ge c^3\) mà a+b+c = 3
Nên \(a^4+b^4+c^4>a^3+b^3+c^3\) (***)
Từ (*);(**);(***) ta có điều phải chứng minh và đẳng thức xảy ra khi a= b=c=1
Tôi có cách chứng minh bằng đồng bậc hóa bất đẳng thức như sau:
ta sẽ chứng minh:
\(3\left(a^4+b^4+c^4\right)>=\left(a+b+c\right)\left(a^3+b^3+c^3\right)\)
<=> \(2\left(a^4+b^4+c^4\right)>=ab\left(a^2+b^2\right)+bc\left(b^2+c^2\right)+ca\left(c^2+a^2\right)\)
mà ta có theo bất đẳng thức AMGM \(a^4+b^4>=\dfrac{\left(a^2+b^2\right)^2}{2}>=\dfrac{2ab\left(a^2+b^2\right)}{2}=ab\left(a^2+b^2\right)\)
làm tương tự rồi cộng lại, ta có đpcm.