Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


7a.
BPT $\Leftrightarrow \frac{x+1987}{2002}-1+\frac{x+1988}{2003}-1> \frac{x+1989}{2004}-1+\frac{x+1990}{2005}-1$
$\Leftrightarrow \frac{x-15}{2002}+\frac{x-15}{2003}> \frac{x-15}{2004}+\frac{x-15}{2005}$
$\Leftrightarrow (x-15)(\frac{1}{2002}+\frac{1}{2003}-\frac{1}{2004}-\frac{1}{2005})>0$
Dễ thấy: $\frac{1}{2002}+\frac{1}{2003}-\frac{1}{2004}-\frac{1}{2005}> 0$
Do đó BPT $\Leftrightarrow x-15>0$
$\Leftrightarrow x>15$
7b.
BPT $\Leftrightarrow (\frac{x-1}{99}-1)+(\frac{x-3}{97}-1)+(\frac{x-5}{95}-1)< (\frac{x-2}{98}-1)+(\frac{x-4}{96}-1)+(\frac{x-6}{94}-1)$
$\Leftrightarrow \frac{x-100}{99}+\frac{x-100}{97}+\frac{x-100}{95}< \frac{x-100}{98}+\frac{x-100}{96}+\frac{x-100}{94}$
$\Leftrightarrow (x-100)(\frac{1}{99}+\frac{1}{97}+\frac{1}{95}-\frac{1}{98}-\frac{1}{96}-\frac{1}{94})<0$
Dễ thấy $\frac{1}{99}+\frac{1}{97}+\frac{1}{95}-\frac{1}{98}-\frac{1}{96}-\frac{1}{94}<0$
Do đó BPT $\Leftrightarrow x-100>0$
$\Leftrightarrow x> 100$


Lời giải:
PT $\Leftrightarrow (x+\frac{1}{y})^2-\frac{2x}{y}=x+\frac{1}{y}=3-\frac{x}{y}$
Đặt $x=a; \frac{1}{y}=b$ thì:
$(a+b)^2-2ab=a+b=3-ab$
$\Rightarrow 2(3-ab)-(a+b)=(a+b)^2-2ab$
$\Leftrightarrow 6-(a+b)=(a+b)^2$
$\Leftrightarrow (a+b)^2+(a+b)-6=0$
$\Leftrightarrow (a+b+3)(a+b-2)=0$
$\Rightarrow a+b=-3$ hoặc $a+b=2$
Nếu $a+b=-3$ thì:
$9-3ab=-3=3-ab\Rightarrow ab=4=6$ (vô lý)
Nếu $a+b=2$ thì:
$4-2ab=2=3-ab\Rightarrow ab=1$
Thay $a=2-b$ vào thì: $(2-b)b=1$
$\Leftrightarrow b^2-2b+1=0\Leftrightarrow (b-1)^2=0$
$\Leftrightarrow b=1$
$\Rightarrow a=2-b=1$
Vậy $(a,b)=(1,1)\Leftrightarrow (x,y)=(1,1)$

Số h/s trung bình của lớp 6B là:
45x7/15=21(h/s)
Lớp 6B có số h/s khá là:
(45-21)x5/8=15(h/s)
Lớp 6B có số h/s xếp loại giỏi là:
45-(21+15)=9(h/s)
Vậy số h/s giỏi của lớp 6B là 9 h/s
Số học sinh trung bình là: 45 \(\times\) \(\dfrac{7}{15}\) = 21 ( học sinh)
Số học sinh còn lại là: 45 - 21 = 24 (học sinh)
Số học sinh khá là: 24 \(\times\) \(\dfrac{5}{8}\) = 15 ( học sinh)
Số học sinh giỏi là: 45 - 21 - 15 = 9 ( học sinh)
Kết luận số học sinh giỏi 9 học sinh

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

Lời giải:
Bạn Dương trả số tiền khi mua túi xách là:
$600000\times \frac{100-30}{100}\times \frac{100-5}{100}=399000$ (đồng)
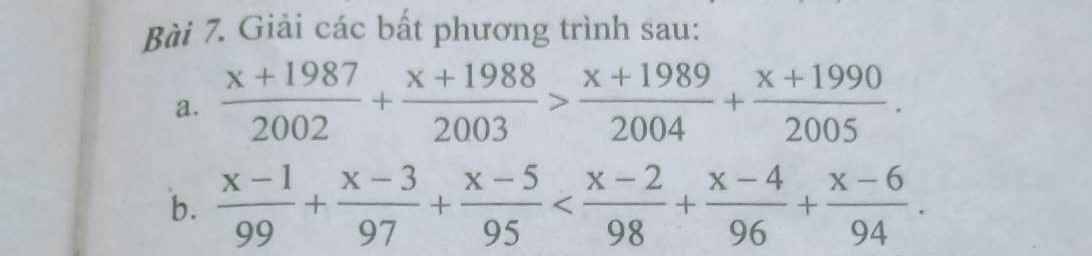


a.
\(\dfrac{x-ab}{a+b}+\dfrac{x-bc}{b+c}+\dfrac{x-ca}{c+a}>a+b+c\)
\(\Leftrightarrow\dfrac{x-ab}{a+b}-c+\dfrac{x-bc}{b+c}-a+\dfrac{x-ac}{a+c}-b>0\)
\(\Leftrightarrow\dfrac{x-ab-ac-bc}{a+b}+\dfrac{x-ab-ac-bc}{b+c}+\dfrac{c-ab-ac-bc}{a+c}>0\)
\(\Leftrightarrow\left(x-ab-ac-bc\right)\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)>0\)
\(\Leftrightarrow x-ab-ac-bc>0\)
\(\Rightarrow x>ab+ac+bc\)
b.
\(\dfrac{a+b-x}{c}+\dfrac{a+c-x}{b}+\dfrac{b+c-x}{a}< \dfrac{-3x}{a+b+c}\)
\(\Leftrightarrow\dfrac{a+b-x}{c}+1+\dfrac{a+c-x}{b}+1+\dfrac{b+c-x}{a}+1< \dfrac{-3x}{a+b+c}+3\)
\(\Leftrightarrow\dfrac{a+b+c-x}{c}+\dfrac{a+b+c-x}{b}+\dfrac{a+b+c-x}{a}< \dfrac{3\left(a+b+c-x\right)}{a+b+c}\)
\(\Leftrightarrow\left(a+b+c-x\right)\left(\dfrac{3}{a+b+c}-\dfrac{1}{a}-\dfrac{1}{b}-\dfrac{1}{c}\right)>0\) (1)
Do \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{9}{a+b+c}\Rightarrow\dfrac{3}{a+b+c}-\dfrac{1}{a}-\dfrac{1}{b}-\dfrac{1}{c}< 0\)
Do đó (1) \(\Leftrightarrow a+b+c-x< 0\)
\(\Rightarrow x>a+b+c\)
8a.
BPT $\Leftrightarrow (\frac{x-ab}{a+b}-c)+(\frac{x-ac}{a+c}-b)+(\frac{x-bc}{b+c}-a)>0$
$\Leftrightarrow \frac{x-(ab+bc+ac)}{a+b}+\frac{x-(ab+bc+ac)}{a+c}+\frac{x-(ab+bc+ac)}{b+c}>0$
$\Leftrightarrow [x-(ab+bc+ac)](\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c})>0$
$\Leftrightarrow x-(ab+bc+ac)>0$ (do $\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}>0$ với $a,b,c$ dương)
$\Leftrightarrow x> ab+bc+ac$