MN giúp mik bài này với ạ.Mik cảm ơn trước:
Cho hình vẽ. Tính các cạnh còn lại của hình thang
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: \(x^2-25=\left(x-5\right)\left(x+5\right)\)
2: \(9x^2-\dfrac{1}{16}y^2=\left(3x\right)^2-\left(\dfrac{1}{4}y\right)^2\)
\(=\left(3x-\dfrac{1}{4}y\right)\left(3x+\dfrac{1}{4}y\right)\)
3: \(x^6-y^4=\left(x^3\right)^2-\left(y^2\right)^2=\left(x^3-y^2\right)\left(x^3+y^2\right)\)
4: \(\left(2x-5\right)^2-64=\left(2x-5-8\right)\left(2x-5+8\right)\)
\(=\left(2x-13\right)\left(2x+3\right)\)
5: \(81-\left(3x+2\right)^2\)
\(=\left(9-3x-2\right)\left(9+3x+2\right)\)
\(=\left(-3x+7\right)\left(3x+11\right)\)
6: \(9\left(x-5y\right)^2-16\left(x+y\right)^2\)
\(=\left(3x-15y\right)^2-\left(4x+4y\right)^2\)
\(=\left(3x-15y-4x-4y\right)\left(3x-15y+4x+4y\right)\)
\(=\left(-x-19y\right)\left(7x-11y\right)\)
7: \(x^3-8=x^3-2^3=\left(x-2\right)\left(x^2+2x+4\right)\)
8: \(27x^3+125y^3=\left(3x\right)^3+\left(5y\right)^3\)
\(=\left(3x+5y\right)\left(9x^2-15xy+25y^2\right)\)
9: \(x^6+216=\left(x^2\right)^3+6^3\)
\(=\left(x^2+6\right)\left(x^4-6x^2+36\right)\)
10: \(x^2+8x+16=x^2+2\cdot x\cdot4+4^2=\left(x+4\right)^2\)
11: \(9x^2-12xy+4y^2\)
\(=\left(3x\right)^2-2\cdot3x\cdot2y+\left(2y\right)^2\)
\(=\left(3x-2y\right)^2\)
12: \(-25x^2y^2+10xy-1\)
\(=-\left[\left(5xy\right)^2-2\cdot5xy\cdot1+1^2\right]\)
\(=-\left(5xy-1\right)^2\)
13: \(x^3-6x^2+12x-8\)
\(=x^3-3\cdot x^2\cdot2+3\cdot x\cdot2^2-2^3\)
\(=\left(x-2\right)^3\)
14: \(8x^3+12x^2y+6xy^2+y^3\)
\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2+y^3\)
\(=\left(2x+y\right)^3\)

\(\left(2x+1\right)\left(4x^2-2x+1\right)-\left(2x-1\right)\left(4x^2+2x+1\right)\)
\(=8x^3+1-\left(8x^3-1\right)=8x^3+1-8x^3+1=2\)

\(C=\left(3x+2\right)^2-\left(3x+2\right)\left(3x-2\right)-6x\)
\(=9x^2+12x+4-\left(9x^2-4\right)-6x=6x+8\)
Vậy bth phụ thuộc biến x, ko có đpcm

\(A=3x\left(x-y\right)-y\left(y-3x\right)\\ =3x^2-3xy-y^2+3xy\\ =3x^2-y^2\\ B=\left(x-y\right)\left(x^2+y^2\right)-\left(x^4y-xy^4\right):xy\\ =\left(x-y\right)\left(x^2+y^2\right)-\left(x^3-y^3\right)\\ =x^3+xy^2-x^2y-y^3-x^3+y^3\\ =xy^2-x^2y\)

Cách 1: Trong tg vuông cạnh đối diện góc \(30^o\) thì bằng nửa cạnh huyền
\(\Rightarrow AB=\dfrac{BC}{2}\Rightarrow BC=2AB\)
Cách 2:
Xét tg vuông ABC có
\(\widehat{B}=90^o-\widehat{C}=60^o\)
Xét tg vuông CEH và tg vuông BEH có
\(\widehat{C}=30^o\)
\(\widehat{EBH}=\dfrac{\widehat{B}}{2}=\dfrac{60^o}{2}=30^o\)
\(\Rightarrow\widehat{C}=\widehat{EBH}\)
EH chung
=> tg CEH = tg BEH (Hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau)
\(\Rightarrow CH=BH\)
Xét tg vuông BEH và tg vuông BAE có
\(\widehat{EBH}=\widehat{EBA}\) (gt)
BE chung
=> tg BEH = tg EBA (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
\(\Rightarrow AB=BH\)
Mà \(BH=CH=\dfrac{BC}{2}\)
\(\Rightarrow AB=\dfrac{BC}{2}\Rightarrow BC=2AB\)

Xét tứ giác HMIK có \(\widehat{H}+\widehat{M}+\widehat{I}+\widehat{K}=360^0\)
=>\(3x+4x+2x+x=360\)
=>\(10x=360^0\)
=>\(x=36^0\)
=>\(\widehat{H}=3\cdot36^0=108^0;\widehat{M}=4\cdot36^0=144^0;\widehat{I}=2\cdot36^0=72^0;\widehat{K}=36^0\)
Vì \(\widehat{H}+\widehat{I}=180^0\)
nên HM//IK
=>HMIK là hình thang

khai triển đa thức ta đc:
=x2-4x+4+x2+4x+4+x3+9x2+27x+27+27x3+27x2+9x+1
=28x3+36x2+36x+36
Vậy hệ số của x2 sau khi khai triển là 36

Bài 1;
a: ABCD là hình thang cân
=>\(\widehat{D}=\widehat{C}=60^0\)
ABCD là hình thang
=>\(\widehat{BAD}+\widehat{ADC}=180^0\)
=>\(\widehat{BAD}=120^0\)
ABCD là hình thang cân
=>\(\widehat{BAD}=\widehat{ABC}\)
=>\(\widehat{ABC}=120^0\)
b: Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
\(\widehat{ADE}=\widehat{BCF}\)
Do đó: ΔAED=ΔBFC
=>AE=BF
Bài 4:
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>BH=CK
Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
c: ΔAHB=ΔAKC
=>AH=AK
Xét ΔABC có \(\dfrac{AH}{AC}=\dfrac{AK}{AB}\)
nên KH//BC
Xét tứ giác BKHC có KH//BC và BH=KC
nên BKHC là hình thang cân

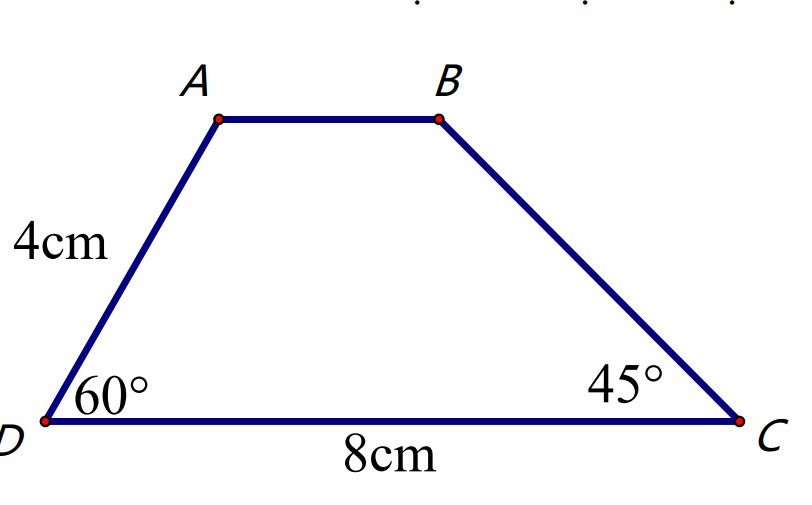
Dựng \(AH\perp CD;BK\perp CD\left(H;K\in CD\right)\)
Xét tg vuông ADH có
\(\widehat{DAH}=90^o-\widehat{D}=30^o\)
\(\Rightarrow DH=\dfrac{AD}{2}=\dfrac{4}{2}=2cm\) (trong tg vuông cạnh đối diện góc \(30^o\) băng nửa cạnh huyền)
\(\Rightarrow AH=\sqrt{AD^2-DH^2}=\sqrt{16-4}=\sqrt{12}=2\sqrt{3}cm\)
\(\Rightarrow AH=BK=2\sqrt{3}cm\) (đường cao của hình thang)
Xét tg vuông BCK có
\(\widehat{KBC}=90^o-\widehat{C}=45^o\)
=> tg BCK vuông cân tại K \(\Rightarrow CK=BK=2\sqrt{3}cm\)
\(\Rightarrow BC=\sqrt{BK^2+CK^2}=\sqrt{12+12}=2\sqrt{6}cm\)
Xét HCN ABKH có
\(AB=KH=CD-DH-CK=8-2\sqrt{3}-2\sqrt{3}=8-4\sqrt{3}=4\left(2-\sqrt{3}\right)cm\)