
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(C=\sqrt{14-8\sqrt{3}}-\sqrt{21-12\sqrt{3}}\)
\(=\sqrt{2\left(7-4\sqrt{3}\right)}-\sqrt{12-2\cdot2\sqrt{3}\cdot3+9}\)
\(=\sqrt{2}\cdot\sqrt{4-2\cdot2\cdot\sqrt{3}+3}-\sqrt{\left(\sqrt{12}-3\right)^2}\)
\(=\sqrt{2}\cdot\sqrt{\left(2-\sqrt{3}\right)^2}-\left|2\sqrt{3}-3\right|\)
\(=\sqrt{2}\cdot\left|2-\sqrt{3}\right|-\left(2\sqrt{3}-3\right)\) (vì \(2\sqrt{3}-3>0\) )
\(=\sqrt{2}\cdot\left(2-\sqrt{3}\right)-2\sqrt{3}+3\) (vì \(2-\sqrt{3}>0\) )
\(=2\sqrt{2}-\sqrt{6}-2\sqrt{3}+3\)

Gọi \(q_1,q_2,...,q_n\left(q_i\inℚ,\forall i=\overline{1,n}\right)\). Theo đề bài, ta có \(q_1q_2...q_n\inℤ\) và \(q_i+q_j\inℤ,\forall i\ne j;i,j=\overline{1,n}\). Không mất tính tổng quát, giả sử \(q_1< q_2< ...< q_n\)
Ta thấy \(q_1+q_2\inℤ\) và \(q_2+q_3\inℤ\) nên \(q_1-q_3\inℤ\). Mà \(q_1+q_3\inℤ\) nên nếu ta đặt \(q_1-q_3=v\) và \(q_1+q_3=u\) với \(u,v\inℤ\) thì \(q_1=\dfrac{u+v}{2};q_3=\dfrac{u-v}{2}\). Do \(q_1+q_2=\dfrac{u+v+2q_2}{2}\) và \(q_3+q_2=\dfrac{u-v+2q_2}{2}\) cũng là các số nguyên, hơn nữa \(u-v\equiv u+v\left(mod2\right)\) nên ta chỉ cần suy ra \(u+v+2q_1⋮2\) hay \(u+v\) là số chẵn, cũng tức là \(q_1=\dfrac{u+v}{2}\) là số nguyên. Một cách tương tự, ta sẽ chứng minh được \(q_i\inℤ,\forall i=\overline{1,n}\) (đpcm)

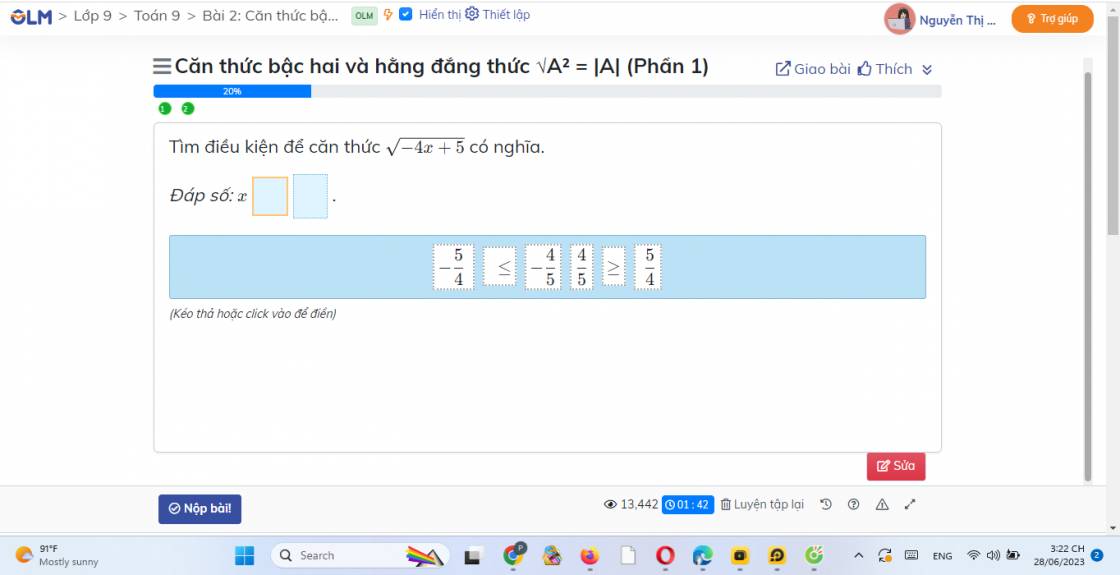
Câu c của em đấy nhé: \(\sqrt{-4x+5}\) có nghĩa ⇔ -4\(x\) + 5 ≥ 0
4\(x\) ≤ 5
\(x\) ≤ \(\dfrac{5}{4}\)
Vậy em kéo dấu ≤ vào ô trống thứ nhất, sau đó em kéo \(\dfrac{5}{4}\) vào ô trống thứ hai rồi ấn nút nộp bài là xong em nhé

Aabb có TLGT là 1Ab:1ab
Nếu Aabb x kiểu gen chỉ cho 1 giao tử duy nhất sẽ cho mô hình phân li kiểu hình 1:1
VD: Aabb x aabb hay Aabb x aaBB

Bài 1: Bài này số nhỏ nên chỉ cần chặn miền giá trị của \(x\) rồi xét các trường hợp thôi nhé. Ta thấy \(3^x< 35\Leftrightarrow x\le3\). Nếu \(x=0\) thì \(VT=2\), vô lí. Nếu \(x=1\) thì \(VT=5\), cũng vô lí. Nếu \(x=2\) thì \(VT=13\), vẫn vô lí. Nếu \(x=3\) thì \(VT=35\), thỏa mãn. Vậy, \(x=3\).
Bài 2: Nếu \(x=0\) thì pt đã cho trở thành \(0!+y!=y!\Leftrightarrow0=1\), vô lí,
Nếu \(x=y\) thì pt trở thành \(2x!=\left(2x\right)!\) \(\Rightarrow\left(x+1\right)\left(x+2\right)...\left(2x\right)=2\) \(\Leftrightarrow x=1\Rightarrow y=1\)
Nếu \(x\ne y\) thì không mất tính tổng quát, giả sử \(1< y< x\) thì \(x!+y!< 2x!\le\left(x+1\right)x!=\left(x+1\right)!< \left(x+y\right)!\) nên pt đã cho không có nghiệm trong trường hợp này.
Như vậy, \(x=y=1\)
Bài 3: Bổ sung đề là pt không có nghiệm nguyên dương nhé, chứ nếu nghiệm nguyên thì rõ ràng \(\left(x,y\right)=\left(0,19\right)\) là một nghiệm cũa pt đã cho rồi.
Giả sử pt đã cho có nghiệm nguyên dương \(\left(x,y\right)\)
Khi đó \(x,y< 19\). Không mất tính tổng quát ta có thể giả sử \(1< y\le x< 19\). Khi ấy \(x^{17}+y^{17}=19^{17}\ge\left(x+1\right)^{17}=x^{17}+17x^{16}+...>x^{17}+17x^{16}\), suy ra \(y^{17}>17x^{16}\ge17y^{16}\) \(\Rightarrow y>17\). Từ đó, ta thu được \(17< y\le x< 19\) nên \(x=y=18\). Thử lại thấy không thỏa mãn.
Vậy pt đã cho không có nghiệm nguyên dương.

a) \(x^2-3xy+3y^2=3y\)
Rõ ràng \(x⋮y\) nên đặt \(x=ky\left(k\inℤ\right)\). Pt trở thành:
\(k^2y^2-3ky^2+3y^2=3y\)
\(\Leftrightarrow\left[{}\begin{matrix}y=0\\k^2y-3ky+3y=3\end{matrix}\right.\).
Khi \(y=0\) \(\Rightarrow x=0\).
Khi \(k^2y-3ky+3y=3\)
\(\Leftrightarrow y\left(k^2-3k+3\right)=3\)
Ta lập bảng giá trị:
| \(y\) | 1 | 3 | -1 | -3 |
| \(k^2-3k+3\) | 3 | 1 | -3 | -1 |
| \(k\) | 0 hoặc 3 | 1 hoặc 2 | vô nghiệm | vô nghiệm |
| \(x\) | 0 (loại) hoặc 3 (nhận) | 3 (nhận) hoặc 6 (nhận) |
Vậy pt đã cho có các nghiệm \(\left(0;0\right);\left(3;1\right);\left(3;3\right);\left(6;3\right)\)
b) \(x^2-2xy+5y^2=y+1\)
\(\Leftrightarrow x^2-2yx+5y^2-y-1=0\)
\(\Delta'=\left(-y\right)^2-\left(5y^2-y-1\right)\) \(=-4y^2+y+1\)
Để pt đã cho có nghiệm thì \(-4y^2+y+1\ge0\), giải bpt thu được \(\dfrac{1-\sqrt{17}}{8}\le y\le\dfrac{1+\sqrt{17}}{8}\). Mà lại có \(-1< \dfrac{1-\sqrt{17}}{8}< 0< \dfrac{1+\sqrt{17}}{8}< 1\) nên suy ra \(y=0\). Từ đó tìm được \(x=\pm1\). Vậy pt đã cho có các nghiệm \(\left(1;0\right);\left(-1;0\right)\)

\(\sqrt{x^2+1}-x=3\\ < =>\sqrt{x^2+1}=3+x\\ < =>\left\{{}\begin{matrix}3+x\ge0\\x^2+1=9+6x+x^2\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}x\ge-3\\6x=-8\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x\ge-3\\x=-\dfrac{4}{3}\left(tm\right)\end{matrix}\right.\\ < =>x=-\dfrac{4}{3}\)
Giải
\(\sqrt{x^2+1}-x=3\\ \Leftrightarrow\sqrt{x^2+1}=3+x\\ \Leftrightarrow\left\{{}\begin{matrix}3+x>0\left(x^2+1\ge0+1=1>0\right)\\x^2+1=\left(3+x\right)^2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>-3\\x^2+1=x^2+6x+9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>-3\\6x=-8\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>-3\\x=-\dfrac{4}{3}\end{matrix}\right.\\ \Leftrightarrow x=-\dfrac{4}{3}\)
Vậy \(S=\left\{-\dfrac{4}{3}\right\}\)

\(\sqrt{\dfrac{45\left(x+y\right)^2.y^2}{16}}\left(dkxd:x\ge0,y\ge0\right)\\ =\dfrac{\sqrt{45\left(x+y\right)^2.y^2}}{\sqrt{16}}\\ =\dfrac{\sqrt{45}.\sqrt{\left(x+y\right)^2}.\sqrt{y^2}}{\sqrt{4^2}}\\ =\dfrac{\sqrt{3^2.5}.\left|x+y\right|.\left|y\right|}{4}\\ =\dfrac{3\sqrt{5}\left(x+y\right).y}{4}\\ =\dfrac{3\sqrt{5}\left(xy+y^2\right)}{4}\)
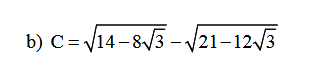

giúp mình bài 3 với ạ