Câu 2:
Cho tam giác ABC có đường trung tuyến AM.TRên AM lấy điểm I sao cho AI=2IM.Tia BI cắt AC tại điểm N
a) Chứng minh AN=NC
b) Trên tia đối của tia NI lấy điểm K sao cho NK=NI. chứng minh CK= 2/3 AM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) M(x) = P(x) + Q(x)
= (x² + 5x - 3) + (2x² - 3x + 1)
= x² + 5x - 3 + 2x² - 3x + 1
= (x² + 2x²) + (5x - 3x) + (-3 + 1)
= 3x² + 2x - 2
b) M(x) - N(x) = 3x² + 2
N(x) = M(x) - (3x² + 2)
= (3x² + 2x - 2) - (3x² + 2)
= 3x² + 2x - 2 - 3x² + 2
= (3x² - 3x²) + 2x + (-2 - 2)
= 2x - 4
Cho N(x) = 0
2x - 4 = 0
2x = 4
x = 4 : 2
x = 2
Vậy nghiệm của đa thức N(x) là x = 2
Yêu cầu bạn @Nguyễn Phương Thảo không sử dụng từ ngữ không văn minh!
Xin chân trọng!

Without the life, most passengers had drowned in that accident - jackets.

\(9x^3-18x=0\)
\(9x\left(x-2\right)=0\)
\(9x=0\) hoặc \(x-2=0\)
*) \(9x=0\)
\(x=0\)
*) \(x-2=0\)
\(x=2\)
Vậy đa thức đã cho có nghiệm \(x=0;x=2\)
9\(x^3\) - 18\(x\) = 0
9.\(x\)(\(x^2\) - 2) = 0
\(\left[{}\begin{matrix}x=0\\x^2-2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\\x=\sqrt{2}\end{matrix}\right.\)
Vậy \(x\) \(\in\) {- \(\sqrt{2}\); 0; \(\sqrt{2}\)}


\(C=-3\left(x-3\right)^2-\left(y-1\right)^2-2021\)
Ta có:
\(\left(x-3\right)^2\ge0\Rightarrow-3\left(x-3\right)^2\le0\)
\(\left(y-1\right)^2\ge0\Rightarrow-\left(y-1\right)^2\le0\)
\(\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2-2021\le-2021\)
Vậy giá trị lớn nhất của C là \(-2021\) khi \(x=3;y=1\)

a: f(x) chia hết cho g(x)
=>\(2x^2-x+2⋮x+1\)
=>\(2x^2+2x-3x-3+5⋮x+1\)
=>\(5⋮x+1\)
=>\(x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-2;4;-6\right\}\)
b: Để f(x) chia hết cho g(x) thì \(3x^2-4x+6⋮3x-1\)
=>\(3x^2-x-3x+1+5⋮3x-1\)
=>\(5⋮3x-1\)
=>\(3x-1\in\left\{1;-1;5;-5\right\}\)
=>\(3x\in\left\{2;0;6;-4\right\}\)
=>\(x\in\left\{\dfrac{2}{3};0;2;-\dfrac{4}{3}\right\}\)
mà x là số nguyên
nên \(x\in\left\{0;2\right\}\)
a) f(x) = 2x² - x + 2
= 2x² + 2x - 3x - 3 + 5
= 2x(x + 1) - 3(x + 1) + 5
Để f(x) chia hết cho g(x) thì 5 ⋮ (x + 1)
⇒ x + 1 ∈ Ư(5) = {-5; -1; 1; 5}
⇒ x ∈ {-6; -2; 0; 4}

Ta có:\(x=100\)
\(\Rightarrow x+1=101\)
\(\Rightarrow M=x^8-\left(x+1\right)x^7+\left(x+1\right)x^6-\left(x+1\right)x^5+...+\left(x+1\right)x^2-\left(x+1\right)x+125\\ \Rightarrow M=x^8-x^8-x^7+x^7+x^6-x^6-x^5+...x^3+x^2-x^2-x+125\\ \Rightarrow M=-x+125\\ \Rightarrow M=-100+125\\ \Rightarrow M=25.\)

a Xét ΔBAD vuông tại A và ΔEAD vuông tại E có
AD chung
\(\widehat{BAD}=\widehat{EAD}\)
Do đó: ΔBAD=ΔEAD
b: Ta có: ΔABD=ΔAED
=>AB=AE và DB=DE
Ta có: AB=AE
=>A nằm trên đường trung trực của BE(1)
Ta có: DB=DE
=>D nằm trên đường trung trực của BE(2)
Từ (1),(2) suy ra AD là đường trung trực của BE
c: Xét ΔDBK vuông tại B và ΔDEC vuông tại E có
DB=DE
BK=EC
Do đó: ΔDBK=ΔDEC
=>\(\widehat{BDK}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{BDE}=180^0\)(hai góc kề bù)
nên \(\widehat{BDE}+\widehat{BDK}=180^0\)
=>E,D,K thẳng hàng
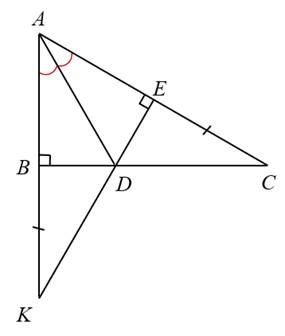
a) Xét và :
.
chung.
.
Suy ra { (cạnh huyền - góc nhọn)
b) Do (câu a) nên + ) (Cặp cạnh tương ứng)
nằm trên đường trung trực của đoạn thẳng (1)
+) (Cặp cạnh tương ứng)
nằm trên đường trung trực của đoạn thẳng (2)
Từ (1) và (2) ta suy ra là đường trung trực của .
c) Xét và :
.
(gt).
.
Suy ra (c.g.c)
Suy ra (Cặp góc tương ứng) (1)
Mặt khác ta có thuộc cạnh nên . (2)
v
Từ (1) và (2) suy ra .
Hay ba điểm thẳng hàng.

a) Cửa hàng đông khách nhất vào thời điểm 11 giờ
Cửa hàng vắng khách nhất vào thời điểm 9 giờ.
b) Số lượt khách đến cửa hàng từ 15 giờ đến 17 giờ tăng 15 lượt khách.
a) Cửa hàng đông khách nhất vào thời điểm 11 giờ
Cửa hàng vắng khách nhất vào thời điểm 9 giờ.
b) Số lượt khách đến cửa hàng từ 15 giờ đến 17 giờ tăng 15 lượt khách.
đây ạ

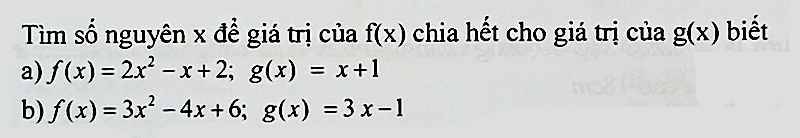

Yêu cầu bạn @Nguyễn Phương Thảo B không sử dụng từ ngữ không văn minh lên diễn đàn!
Xin trân trọng!
a: Ta có: AI+IM=MA
=>AM=2IM+IM=3IM
=>\(\dfrac{AI}{AM}=\dfrac{2}{3}\)
Xét ΔABC có
AM là đường trung tuyến
\(AI=\dfrac{2}{3}AM\)
Do đó: I là trọng tâm của ΔABC
Xét ΔABC có
I là trọng tâm
BI cắt AC tại N
Do đó: N là trung điểm của AC
=>NA=NC
b:
Xét ΔNAI và ΔNCK có
NA=NC
\(\widehat{ANI}=\widehat{CNK}\)(hai góc đối đỉnh)
NI=NK
Do đó: ΔNAI=ΔNCK
=>CK=AI
=>\(CK=\dfrac{2}{3}AM\)