cho a=4 .tìm các giá trị sau :căn bậc 2 số học của a , giá trị tuyệt đối của a,luỹ thừa bậc 3 của a. giupk minh voi . nhanh nhé mình đang gấp.mnkcamr ơn nhiều🥰.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


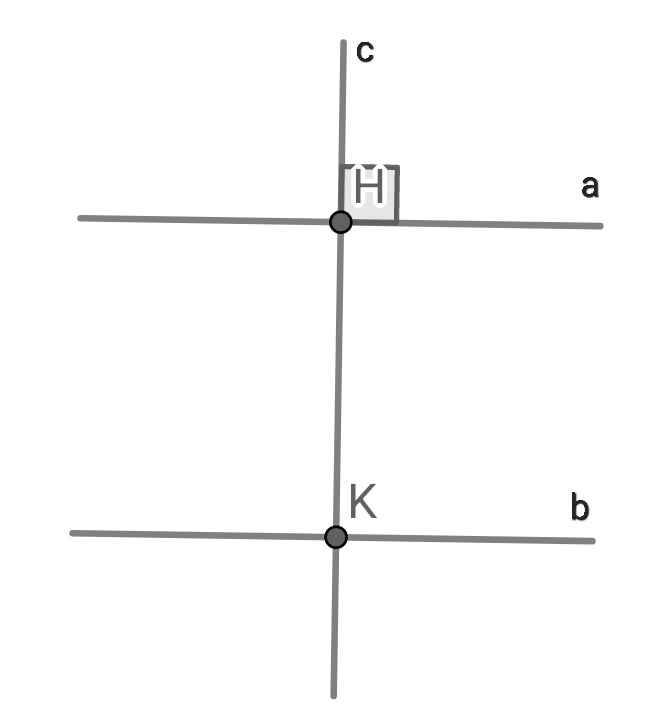 GT a // b, c ⊥ a
GT a // b, c ⊥ a
KL c ⊥ b
Chứng minh:
Do a // b
⇒ ∠bKH = ∠aHc (đồng vị)
Mà ∠aHc = 90⁰ (do c ⊥ a)
⇒ ∠bKG = 90⁰
Vậy c ⊥ b

\(\left(-2\right)^{190}=2^{190}>2^{182}=\left(2^7\right)^{26}=128^{26}\)
\(128^{26}>125^{26}=\left(5^3\right)^{26}=5^{78}>5^{76}\)
\(\Rightarrow\left(-2\right)^{190}>5^{76}\)
5⁷⁶ = (5²)³⁸ = 25³⁸
(-2)¹⁹⁰ = 2¹⁹⁰ = (2⁵)³⁸ = 32³⁸
Do 26 < 32 nên 25³⁸ < 32³⁸
⇒ 5⁷⁶ < (-2)¹⁹⁰

Lời giải:
a. $\frac{2-x}{4}=\frac{3x-1}{3}$
$\Rightarrow 3(2-x)=4(3x-1)$
$\Rightarrow 6-3x=12x-4$
$\Rightarrow 6+4=12x+3x$
$\Rightarrow 10=15x$
$\Rightarrow x=\frac{10}{15}=\frac{2}{3}$
b.
$\frac{x}{7}=\frac{x+16}{35}$
$\Rightarrow \frac{5x}{35}=\frac{x+16}{35}$
$\Rightarrow 5x=x+16$
$\Rightarrow 4x=16$
$\Rightarrow x=4$
c.
$\sqrt{x^2+1}=3$
$\Rightarrow x^2+1=9$
$\Rightarrow x^2=8\Rightarrow x=\pm \sqrt{8}=\pm 2\sqrt{2}$

Lời giải:
$3^6-M=3^0+3^1+3^2+3^3+3^4+3^5$
$3(3^6-M)=3^1+3^2+3^3+3^4+3^5+3^6$
$\Rightarrow 3(3^6-M)-(3^6-M)=3^6-3^0$
$\Rightarrow 2(3^6-M)=3^6-1$
$\Rightarrow 2M = 2.3^6-(3^6-1)=3^6+1$
$\Rightarrow M=\frac{3^6+1}{2}$
M=36-(35+34+...+31+30)
Đặt A=35+34+...+31+30
3A=36+35+...+32+31
3A-A=36+35+...+32+31-35-34-...-31-30
2A=36-30=>A=\(\dfrac{3^6-3^0}{2}\)
Thay A vào M ta có:
M=36-\(\dfrac{3^6-3^0}{2}\)
M=\(\dfrac{2.3^6}{2}\)-\(\dfrac{3^6-3^0}{2}\)
M=\(\dfrac{3^6.\left(2-1\right)-1}{2}\)
M=\(\dfrac{3^6.1-1}{2}\)
M=\(\dfrac{3^6-1}{2}\)
M=364

Lời giải:
$A=\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+....+\frac{1}{3^{99}}$
$3A=1+\frac{1}{3}+\frac{1}{3^2}+....+\frac{1}{3^{98}}$
$\Rightarrow 3A-A=1-\frac{1}{3^{99}}< 1$
$\Rightarrow 2A< 1\Rightarrow A< \frac{1}{2}$
A = \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\) + ... + \(\dfrac{1}{3^{99}}\)
3A = 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + ... + \(\dfrac{1}{3^{98}}\)
3A - A = ( 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + ... + \(\dfrac{1}{3^{98}}\)) - (\(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + ... + \(\dfrac{1}{3^{98}}\) - \(\dfrac{1}{3^{99}}\))
2A = 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + ... + \(\dfrac{1}{3^{98}}\) - \(\dfrac{1}{3}\) - \(\dfrac{1}{3^2}\) - ... - \(\dfrac{1}{3^{98}}\) - \(\dfrac{1}{3^{99}}\)
2A = ( \(\dfrac{1}{3}\) - \(\dfrac{1}{3}\)) + (\(\dfrac{1}{3^2}\) - \(\dfrac{1}{3^2}\)) + ... + (1 - \(\dfrac{1}{3^{99}}\))
2A = 0 + 0 + ... + 0 + 1 - \(\dfrac{1}{3^{99}}\)
2A = (1 - \(\dfrac{1}{3^{99}}\))
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{2.3^{99}}\) < \(\dfrac{1}{2}\)

Giá tiền mỗi bó hoa sau khi giảm:
\(85000-85000.15\%=72250\) (đồng)
Giá tiền 9 bó hoa đầu tiên:
\(72250.9=650250\) (đồng)
Giá tiền 36 bó hoa còn lại:
\(36.72250.80\%=2080800\) (đồng)
Tổng số tiền công ty phải trả:
\(2080800+650250=2731050\) (đồng)

Nếu không có thêm điều kiện gì thì biểu thức này không có giá trị lớn nhất bạn nhé.

a) \(4.\left(-\dfrac{1}{2}\right)^3-2.\left(-\dfrac{1}{2}\right)^2+3.\left(-\dfrac{1}{2}\right)+1\)
\(=4.\left(-\dfrac{1}{8}\right)-2.\dfrac{1}{4}+3.\left(-\dfrac{1}{2}\right)+1\)
\(=-\dfrac{1}{2}-\dfrac{1}{2}-\dfrac{3}{2}+1\)
\(=-\dfrac{3}{2}\)
b) \(8.\sqrt{9}-\sqrt{64}\)
\(=8.3-8\)
\(=24-8\)
\(=16\)
c) \(\sqrt{\dfrac{9}{16}}+\dfrac{25}{46}:\dfrac{5}{23}-\dfrac{7}{4}\)
\(=\dfrac{3}{4}+\dfrac{5}{2}-\dfrac{7}{4}\)
\(=-1+\dfrac{5}{2}\)
\(=\dfrac{3}{2}\)

a) 2/3 + 3/4 . (-4/9)
= 2/3 - 1/3
= 1/3
b) -5/7 . 31/33 + (-5/7) : 33/2
= -5/7 . 31/33 - 5/7 . 2/33
= -5/7 . (31/33 + 2/33)
= -5/7 . 1
= -5/7
c) -3/5 . 13/11 - (-3/5) . 2/11
= -3/5 . (13/11 - 2/11)
= -3/5 . 1
= -3/5
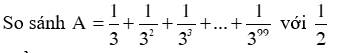
Lời giải:
Căn bậc 2 số học của $a$: $\sqrt{4}=2$
Giá trị tuyệt đối của $a$: $|a|=|4|=4$
Lũy thừa bậc 3 của $a$: $a^3=4^3=64$