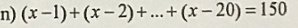
Giúp mình câu này ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) $x^2+6x+9$
$=x^2+2.x.3+3^2$
$=(x+3)^2$
b) $9x^2-6x+1$
$=(3x)^2-2.3x.1+1^2$
$=(3x-1)^2$
c) $x^2y^2+xy+\frac14$
$=(xy)^2+2.xy.\frac12+\left(\frac12\right)^2$
$=\left(xy+\frac12\right)^2$
d) $(x-y)^2+6(x-y)+9$
$=(x-y)^2+2.(x-y).3+3^2$
$=(x-y+3)^2$
Bài 2:
a) $-x^3+3x^2-3x+1$
$=1^3-3.1^2.x+3.1.x^2-x^3$
$=(1-x)^3$
b) $x^3+x^2+\frac13 x+\frac{1}{27}$
$=x^3+3.x^2.\frac13+3.x.\left(\frac13\right)^2+\left(\frac13\right)^3$
$=\left(x+\frac13\right)^3$
c) $x^6-3x^4y+3x^2y^2-y^3$
$=(x^2)^3-3.(x^2)^2.y+3.x^2.y^2-y^3$
$=(x^2-y)^3$
d) $(x-y)^3+(x-y)^2+\frac13 (x-y)+\frac{1}{27}$
$=(x-y)^3+3.(x-y)^2.\frac13+3.(x-y).\left(\frac13\right)^2+\left(\frac13\right)^3$
$=\left(x-y+\frac13\right)^3$
Bài 3:
a) $x^3+27$
$=x^3+3^3$
$=(x+3)(x^2-x.3+3^2)$
$=(x+3)(x^2-3x+9)$
b) $x^3-\frac18$
$=x^3-\left(\frac12\right)^3$
$=\left(x-\frac12\right)\left[x^2-x.\frac12+\left(\frac12\right)^2\right]$
$=\left(x-\frac12\right)\left(x^2-\frac12 x+\frac14\right)$
c) $8x^3+y^3$
$=(2x)^3+y^3$
$=(2x+y)[(2x)^2-2x.y+y^2]$
$=(2x+y)(4x^2-2xy+y^2)$
d) $8x^3-27y^3$
$=(2x)^3-(3y)^3$
$=(2x-3y)[(2x)^2+2x.3y+(3y)^2]$
$=(2x-3y)(4x^2+6xy+9y^2)$
Bài 4:
a) \(101^2=\left(100+1\right)^2\)
\(=100^2+2.100.1+1^2\)
\(=10000+200+1=10201\)
b) \(75^2-50.75+25^2\)
\(=75^2-2.75.25+25^2\)
\(=\left(75-25\right)^2\)
\(=50^2=2500\)
c) \(103.97\)
\(=\left(100+3\right).\left(100-3\right)\)
\(=100^2-3^2\\ =10000-9=9991\)
Bài 5:
a) \(\left(x+3y\right)^2-\left(x-3y\right)^2\)
\(=\left(x+3y-x+3y\right)\left(x+3y+x-3y\right)\\ =6y.2x=12xy\)
b) \(Q=\left(x-y\right)^2-4\left(x-y\right)\left(x+2y\right)+4\left(x+2y\right)^2\)
\(=\left(x-y\right)^2-2.\left(x-y\right).2\left(x+2y\right)+\left[2\left(x+2y\right)\right]^2\\ =\left[\left(x-y\right)-2\left(x+2y\right)\right]^2\\ =\left(x-y-2x-4y\right)^2\\ =\left(-x-5y\right)^2\)
c) \(A=\left(x+2\right)^3+\left(x-2\right)^3-2x\left(x^2+12\right)\)
\(=\left(x+2+x-2\right)\left[\left(x+2\right)^2-\left(x+2\right)\left(x-2\right)+\left(x-2\right)^2\right]-2x\left(x^2+12\right)\\ =2x\left(x^2+4x+4-x^2+4+x^2-4x+4\right)-2x\left(x^2+12\right)\\ =2x\left(x^2+12\right)-2x\left(x^2+12\right)=0\)
d) \(B=\left(xy+2\right)^3-6\left(xy+2\right)^2+12\left(xy+2\right)-8\)
\(=\left(xy+2\right)^3-3.\left(xy+2\right)^2.2+3.\left(xy+2\right).2^2-2^3\\ =\left(xy+2-2\right)^3\\ =\left(xy\right)^3=x^3y^3\)
e) \(A=\left(x-3\right)\left(x^2+3x+9\right)-\left(x^3+3\right)\)
\(=\left(x-3\right)\left(x^2+x.3+3^2\right)-x^3-3\\ =x^3-3^3-x^3-3\\ =-27-3=-30\)
Bài 6:
\(a,VT=\left(a-b\right)^2=a^2-2ab+b^2\\ =\left(a^2+2ab+b^2\right)-4ab\\ =\left(a+b\right)^2-4ab=VP\\ b,VT=\left(x+y\right)^2+\left(x-y\right)^2\\ =x^2+2xy+y^2+x^2-2xy+y^2\\ =2x^2+2y^2\\ =2\left(x^2+y^2\right)=VP\\ c,VT=\left(x+y\right)^2-\left(x-y\right)^2\\ =\left[\left(x+y\right)-\left(x-y\right)\right]\left[\left(x+y\right)+\left(x-y\right)\right]\\ =\left(x+y-x+y\right)\left(x+y+x-y\right)\\ =2y.2x=4xy=VP\\ d,VT=\left(x-y\right)^2+\left(x+y\right)^2+2\left(x^2-y^2\right)\\ =\left(x-y\right)^2+2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\\ =\left[\left(x-y\right)+\left(x+y\right)\right]^2\\ =\left(x-y+x+y\right)^2\\ =\left(2x\right)^2=4x^2=VP\)

Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}ab\cdot sinC=\dfrac{1}{2}\cdot7\cdot23\cdot sin130^o=61,7\) (đvdt)

Bài 14:
Số bao đường ở mỗi kho ban đầu là:
168:3=56(bao)
Số bao đường ở mỗi kho sau đó là:
56+16=72(bao)
Số bao đường đã bán hết là:
72x2=144(bao)

7A: Các số có 4 chữ số có tổng các chữ số bằng 4 là:
4000;
3001;3100;3010;1300;1030;1003;
2020;2200;2002;
1120;1210;2110;1102;1201;2101;1012;1021;2011
=>Có 1+6+3+9=19(số)
b: Tổng của các số là:
4000+3001+3100+3010+1300+1030+1003+2020+2200+2002+1120+1210+2110+1102+1201+2101+1012+1021+2011
=35554

5B:
Số chữ số dùng để đánh số cho trang có 1 chữ số là:
(9-1+1)x1=9(chữ số)
Số chữ số dùng để đánh số cho trang có 2 chữ số là:
(99-10+1)x2=180(chữ số)
Số chữ số dùng để đánh số cho trang có 3 chữ số là:
\(\left(145-100+1\right)\cdot3=46\cdot3=138\)(chữ số)
Tổng số chữ số cần dùng là:
138+9+180=327(chữ số)
5A:
Số chữ số dùng để đánh số cho trang có 1 chữ số là:
(9-1+1)x1=9(chữ số)
Số chữ số dùng để đánh số cho trang có 2 chữ số là:
(99-10+1)x2=180(chữ số)
Số chữ số dùng để đánh số cho trang có 3 chữ số là:
\(\left(256-100+1\right)\cdot3=471\)(chữ số)
Tổng số chữ số cần dùng là:
471+180+9=660(chữ số)

a: Ta có: \(\widehat{xOy}=\widehat{mOn}\)(hai góc đối đỉnh)
mà \(\widehat{xOy}=50^0\)
nên \(\widehat{mOn}=50^0\)
Ta có: \(\widehat{xOy}+\widehat{mOy}=180^0\)(hai góc kề bù)
=>\(\widehat{mOy}+50^0=180^0\)
=>\(\widehat{mOy}=130^0\)
Ta có: \(\widehat{xOn}=\widehat{mOy}\)(hai góc đối đỉnh)
mà \(\widehat{mOy}=130^0\)
nên \(\widehat{xOn}=130^0\)
b: Oa là phân giác của góc xOy
=>\(\widehat{yOa}=\dfrac{\widehat{xOy}}{2}=25^0\)
Ta có: Ob là phân giác của góc yOm
=>\(\widehat{yOb}=\dfrac{\widehat{yOm}}{2}=65^0\)
Ta có: \(\widehat{aOb}=\widehat{aOy}+\widehat{bOy}=25^0+65^0=90^0\)
\(\left(x-1\right)+\left(x-2\right)+...+\left(x-20\right)=150\\ x-1+x-2+...+x-20=150\\ \left(x+x+...+x\right)-\left(1+2+...+20\right)\\ 20\cdot x-\left[\left(20-1\right):1+1\right]\cdot\left(20+1\right):2=150\\ 20\cdot x-20\cdot21:2=150\\ 20\cdot x-210=150\\ 20\cdot x=150+210\\ 20\cdot x=360\\ x=360:20\\ x=18\)