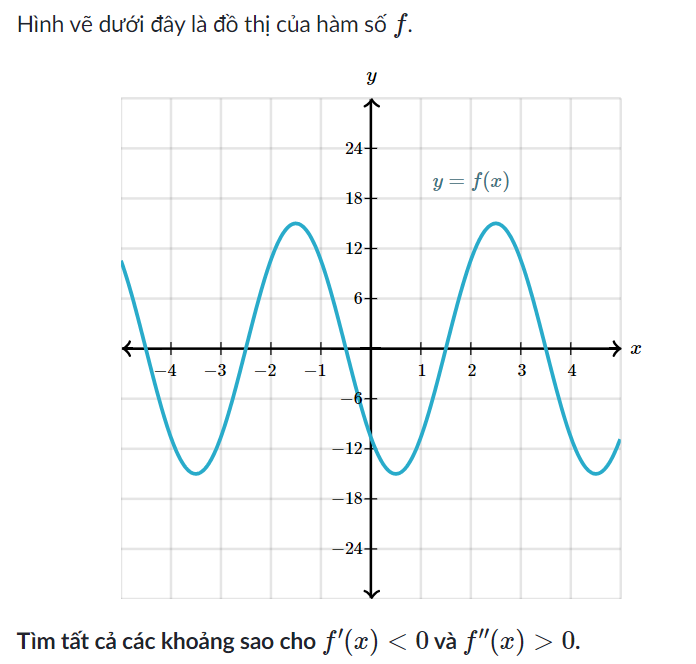
Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [ -20;20] để hàm số |2x³ - 3(2m+3)x² + 6m(m+3)x| đồng biến trên khoảng (0;2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đề thi đánh giá năng lực
NQ
Ngô Quyết
VIP
27 tháng 7 2024
Bạn chỉ cần vào lĩnh vực mà mik yêu thích để có tiến bộ thì sau đó sẽ giỏi
27 tháng 7 2024
\(y=\dfrac{x^2-\left(x^2+4mx+1\right)}{x+\sqrt{x^2+4mx+1}}=\dfrac{-4mx-1}{x+\sqrt{x^2+4mx+1}}\)
\(=\dfrac{-4mx-1}{x+\left|x\right|\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}\)
\(\lim\limits_{x\rightarrow\pm\infty}y\dfrac{-4m-\dfrac{1}{x}}{1\pm\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}=-4m\)
Để y = 1 là TCN => -4m = 1 => m = -1/4
20 tháng 7 2024
a, Ta có (AC;AB) = ^BAC
tan^BAC = BC/AB = 1 => ^BAC = 450
b, Ta có BD // B'D'
=> (AD';BD) = (AD';B'D') = ^AD'B'
Xét tam giác AD'B' ta có AB' = B'D' = AD'
=> tam giác AD'B' đều => ^AD'B' = 600
c, Ta có BD vuông AC ; BD vuông CC'
=> BD vuông (ACC')
Mà AC' thuộc (ACC') => AC' vuông BD
4 tháng 7 2024
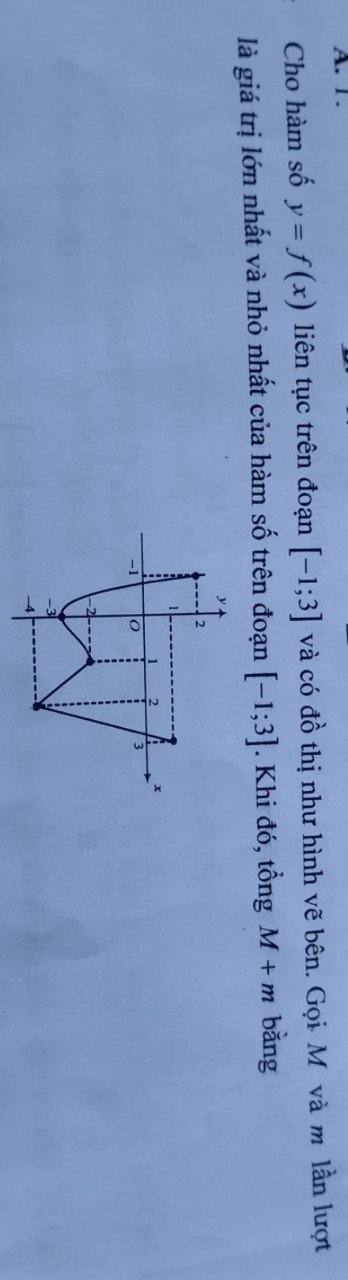
Dựa vào đồ thị, ta thấy \(m=\min\limits_{\left[-1;3\right]}f\left(x\right)=f\left(2\right)=-4\)
và \(M=\max\limits_{\left[-1;3\right]}f\left(x\right)=f\left(-1\right)=2\)
Khi đó \(M+m=2-4=-2\)