trên đường thẳng xy lấy điểm O.Trên tia Ox lấy điểm Asao cho OA =3cm ,trên tia Oy lấy điểm B sao cho OB=2cm. a| Kể tên hai tia trùng gốc B;hai tia đối nhau gốc O;ba đoạn thẳng trên hình vẽ. b| Điểm O có phải là trung điểm của đoạn thẳng AB không?vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=2^1+2^2+...+2^{76}+2^{77}\)
=>\(2A=2^2+2^3+...+2^{77}+2^{78}\)
=>\(2A-A=2^2+2^3+...+2^{77}+2^{78}-2^1-2^2-...-2^{76}-2^{77}\)
=>\(A=2^{78}-2\)

ta có số phần chỉ m vải bán ngày 3 là
1-2/7-3/5=4/35
3 ngày bán số m là
40:4/35=350m
đáp số :350m vải

Sau lần 1 thì số gạo còn lại chiếm:
1-25%=75%(tổng số)
Sau lần 2 thì số gạo còn lại chiếm:
\(75\%\left(1-40\%\right)=\dfrac{3}{4}\cdot\dfrac{3}{5}=\dfrac{9}{20}\)(tổng số gạo)
Tổng số gạo là \(54:\dfrac{9}{20}=54\cdot\dfrac{20}{9}=120\left(kg\right)\)
Lần 1 bán được: \(120\cdot25\%=30\left(kg\right)\)
lần 2 bán được:
120-30-54=90-54=36(kg)


\(5A=\dfrac{5^{2021}+5}{5^{2021}+1}=1+\dfrac{4}{5^{2021}+1}\)
\(5B=\dfrac{5^{2020}+5}{5^{2020}+1}=1+\dfrac{4}{5^{2020}+1}\)
Ta có: \(5^{2021}+1>5^{2020}+1\)
=>\(\dfrac{4}{5^{2021}+1}< \dfrac{4}{5^{2020}+1}\)
=>\(\dfrac{4}{5^{2021}+1}+1< \dfrac{4}{5^{2020}+1}+1\)
=>5A<5B
=>A<B

3(x-2)-5(3-x)=3
=>\(3x-6-15+5x=3\)
=>\(8x-21=3\)
=>\(8x=24\)
=>\(x=\dfrac{24}{8}=3\)
Không quy đồng hãy tính tổng sau: A= 1/20 + 1/30 + 1/42 + 1/56 + 1/72 + 1/90. Các bạn giúp mình với.

\(A=\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\)
\(A=\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}\)
\(A=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\)
\(A=\dfrac{1}{4}-\dfrac{1}{10}\)
\(A=\dfrac{10}{40}-\dfrac{4}{40}\)
\(A=\dfrac{8}{40}=\dfrac{1}{5}\)
Vậy \(A=\dfrac{1}{5}\)
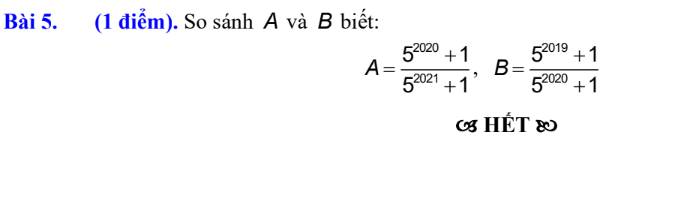
a: Hai tia trùng nhau gốc B là BO,Bx
Hai tia đối nhau gốc O là Ox,Oy
Ba đoạn thẳng là OA,BO,AB
Vì OA và OB là hai tia đối nhau
nên O nằm giữa A và B
mà OA>OB
nên O không là trung điểm của AB
ai đó làm hộ tui được không?