Kẻ DH//CE(H\(\in\)BC)

Ta có: DH//CE

=>\(\widehat{DHB}=\widehat{ACB}\)

mà \(\widehat{ACB}=\widehat{DBH}\)(ΔABC cân tại A)

nên \(\widehat{DHB}=\widehat{DBH}\)

=>DH=DB

mà DB=CE

nên DH=CE

Xét tứ giác DHEC có

DH//EC

DH=EC

Do đó: DHEC là hình bình hành

=>DE cắt HC tại trung điểm của mỗi đường

mà I là trung điểm của DE

nên I là trung điểm của HC

=>H,I,C thẳng hàng

mà B,H,C thẳng hàng

nên B,I,C thẳng hàng

a: Xét ΔABC vuông tại A và ΔADC vuông tại A có

AB=AD

AC chung

Do đó; ΔABC=ΔADC

=>CB=CD

=>ΔCBD cân tại C

b: Ta có: AD=AB

mà AB<BC(ΔABC vuông tại A)

nên AD<BC

Đề thiếu yêu cầu đề bài. Bạn xem lại nhé.

\(x^2-5x+6=0\)

=>\(x^2-2x-3x+6=0\)

=>x(x-2)-3(x-2)=0

=>(x-2)(x-3)=0

=>\(\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)

=>Nghiệm của phương trình là giá trị của biến sao cho tại giá trị đó, đa thức đó có giá trị bằng 0

\(\dfrac{x-1}{3}=\dfrac{x+3}{5}\)

=>5(x-1)=3(x+3)

=>5x-5=3x+9

=>2x=14

=>x=14:2=7

-5 có âm không ? 

a: \(\dfrac{2x-5}{x+3}=-9\)

=>-9(x+3)=2x-5

=>-9x-27=2x-5

=>-11x=22

=>\(x=-\dfrac{22}{11}=-2\)

b: Sửa đề: \(\left(x+1\right)^4=\left(x+1\right)^2\)

=>\(\left(x+1\right)^4-\left(x+1\right)^2=0\)

=>\(\left(x+1\right)^2\left[\left(x+1\right)^2-1\right]=0\)

=>\(\left(x+1\right)^2\left(x+1-1\right)\left(x+1+1\right)=0\)

=>\(x\left(x+2\right)\left(x+1\right)^2=0\)

=>\(\left[{}\begin{matrix}x=0\\x=-2\\x=-1\end{matrix}\right.\)

Tổng các số x thỏa mãn là:

0+(-2)+(-1)=-3

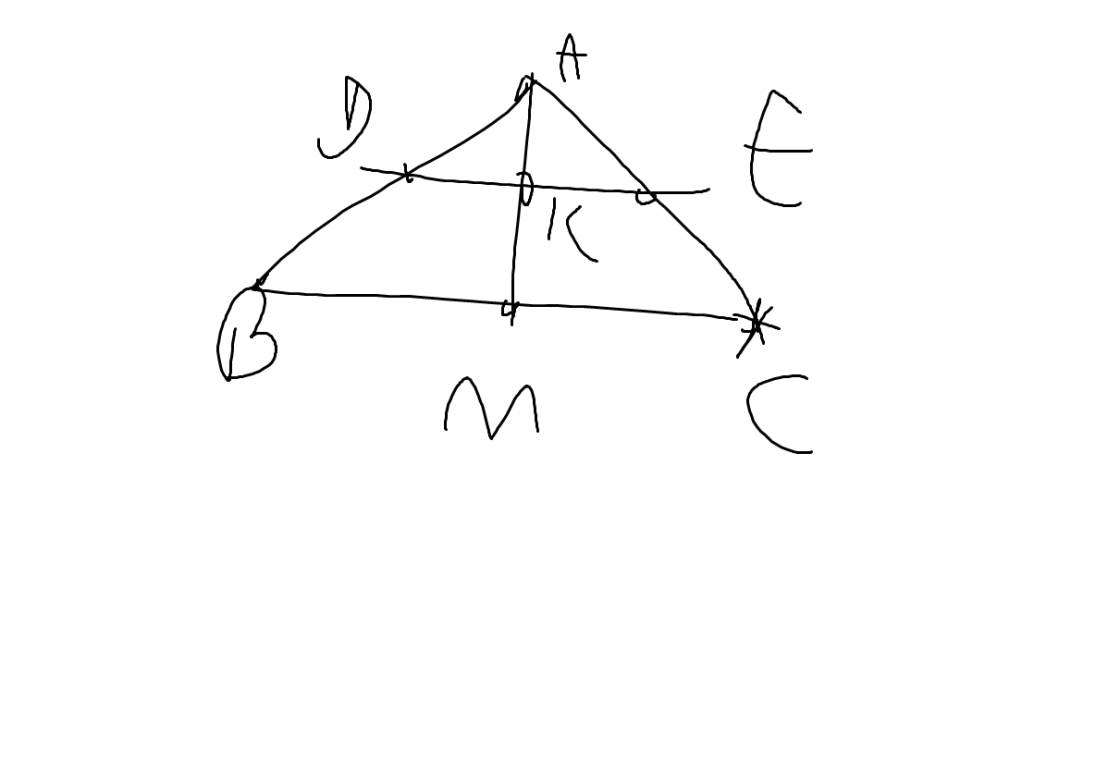
a: Xét ΔAMB và ΔAMC có

AB=AC

AM chung

MB=MC

Do đó: ΔAMB=ΔAMC

b: Ta có: ΔAMB=ΔAMC

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AM\(\perp\)BC

Ta có: ΔAMB=ΔAMC

=>\(\widehat{MAB}=\widehat{MAC}\)

=>AM là phân giác của góc BAC

c: Xét ΔADE có AD=AE

nên ΔADE cân tại A

Ta có: ΔADE cân tại A

mà AK là đường phân giác

nên AK\(\perp\)DE

Em cần làm gì với biểu thức này?

Chắc là phải tính đấy cô Thương Hoài