chứng tỏ răng 2n+1 và n.(n+1) là hai số nguyên tố cùng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số học sinh giỏi là \(50\cdot20\%=10\left(bạn\right)\)
Số học sinh khá là \(10:\dfrac{7}{20}=10\cdot\dfrac{20}{7}=\dfrac{200}{7}\)
=>Đề sai rồi bạn

`#3107.101107`
Số học sinh lớp `6A` bằng tổng số hs lớp `6B; 6C?`
`=>` Số hs lớp `6A =`\(\dfrac{1}{2}\) tổng số hs lớp `6B; 6C`
`=>` Số hs lớp `6A =`\(\dfrac{1}{3}\) tổng số hs các lớp
Số học sinh lớp 6A là:
\(\dfrac{1}{3}\cdot135=45\left(\text{học sinh}\right)\)
Tổng số hs 2 lớp 6B và 6C là:
`135 - 45 = 90 (\text{học sinh})`
Số học sinh lớp 6B là:
\(\dfrac{90+2}{2}=46\left(\text{học sinh}\right)\)
Số học sinh lớp 6C là:
`90 - 46 = 44 (\text{học sinh}).`

** Bổ sung điều kiện $x,y$ là số tự nhiên.
Lời giải:
Do $(x^2+1)(x+1)=3^y$ nên tồn tại $m,n$ tự nhiên, $m+n=y$ sao cho:
$x^2+1=3^m, x+1=3^n$
$\Rightarrow (3^n-1)^2+1=3^m$
$\Rightarrow 3^{2n}-2.3^n+2=3^m$
Nếu $m,n$ đều dương thì $2=3^m+2.3^n-3^{2n}\vdots 3$ (vô lý)
Do đó trong 2 số $m,n$ tồn tại ít nhất 1 số bằng $0$
Nếu $m=0$ thì: $x^2+1=3^0=1\Rightarrow x=0$
$\Rightarrow y=0$. Vậy $(x,y)=(0,0)$
Nếu $n=0$ thì $x+1=3^0=1\Rightarrow x=0$
$\Rightarrow y=0\Rightarrow (x,y)=(0,0)$
Vậy $(x,y)=(0,0)$

bạn ợi thêm 15 quả là bán 1/3 quả rồi bán được thêm 15 quả nữa à

\(\dfrac{9}{13}\cdot\dfrac{10}{3}-\dfrac{9}{13}:\dfrac{3}{20}+\dfrac{-9}{13}\)
\(=\dfrac{9}{13}\cdot\dfrac{10}{3}-\dfrac{9}{13}\cdot\dfrac{20}{3}-\dfrac{9}{13}\)
\(=\dfrac{9}{13}\left(\dfrac{10}{3}-\dfrac{20}{3}-1\right)=\dfrac{9}{13}\cdot\dfrac{-13}{3}=-\dfrac{9}{3}=-3\)

a: Số học sinh nam là:
40-27=13(bạn)
Tỉ số giữa số học sinh nữ và số học sinh nam là:
\(27:13=\dfrac{27}{13}\)
b: Số học sinh nữ chiếm:
\(\dfrac{13}{40}=32,5\%\)

a: \(x-\dfrac{1}{5}=\dfrac{2}{11}\)
=>\(x=\dfrac{2}{11}+\dfrac{1}{5}=\dfrac{10}{55}+\dfrac{11}{55}=\dfrac{21}{55}\)
b: \(\dfrac{x}{5}=\dfrac{5}{6}+\dfrac{-19}{30}\)
=>\(\dfrac{x}{5}=\dfrac{25-19}{30}=\dfrac{6}{30}=\dfrac{1}{5}\)
=>x=1
c: Đề thiếu vế phải rồi bạn
d: \(\dfrac{11}{8}+\dfrac{13}{6}=\dfrac{85}{x}\)
=>\(\dfrac{85}{x}=\dfrac{11\cdot3+13\cdot4}{24}=\dfrac{85}{24}\)
=>x=24
e: \(x-\dfrac{-6}{15}=\dfrac{4}{27}\)
=>\(x+\dfrac{2}{5}=\dfrac{4}{27}\)
=>\(x=\dfrac{4}{27}-\dfrac{2}{5}=\dfrac{20-54}{135}=\dfrac{-34}{135}\)
f: \(x-\dfrac{4}{6}=\dfrac{5}{25}+\dfrac{-7}{15}\)
=>\(x-\dfrac{2}{3}=\dfrac{1}{5}+\dfrac{-7}{15}=\dfrac{-4}{15}\)
=>\(x=-\dfrac{4}{15}+\dfrac{2}{3}=\dfrac{-4}{15}+\dfrac{10}{15}=\dfrac{6}{15}=\dfrac{2}{5}\)
g: \(-\dfrac{-7}{5}+x=\dfrac{4}{9}\)
=>\(x+\dfrac{7}{5}=\dfrac{4}{9}\)
=>\(x=\dfrac{4}{9}-\dfrac{7}{5}=\dfrac{20-63}{45}=\dfrac{-43}{45}\)
a, \(x-\dfrac{1}{5}=\dfrac{2}{11}\)
\(x=\dfrac{2}{11}+\dfrac{1}{5}\)
\(x=\dfrac{21}{55}\)
b, \(\dfrac{x}{5}=\dfrac{5}{6}+\dfrac{\left(-19\right)}{30}\)
\(\dfrac{x}{5}=\dfrac{1}{5}\)
=> x = 1
gửi bạn câu a và b trước, lát mình gửi những câu còn lại sau nhé

\(\dfrac{x+10}{x+17}=\dfrac{3}{4}\)
=>\(4\left(x+10\right)=3\left(x+17\right)\)
=>\(4x+40=3x+51\)
=>4x-3x=51-40
=>x=11(nhận)

(0,5x - 2,5) .(3,5 - x ) = 0
= > Suy ra ta có 2 trường hợp: TH1: (0,5x - 2,5) = 0
TH2 : (3,5- x ) = 0
= > Biểu thức này = 0
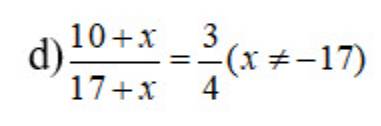
X+Y = 0