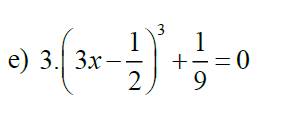
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta thấy :
\(\dfrac{3}{10}>\dfrac{3}{15}\)
\(\dfrac{3}{11}>\dfrac{3}{15}\)
\(\dfrac{3}{12}>\dfrac{3}{15}\)
\(\dfrac{3}{13}>\dfrac{3}{15}\)
\(\dfrac{3}{14}>\dfrac{3}{15}\)
\(\Rightarrow S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}>5.\dfrac{3}{15}\) (1)
\(S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{1}{14}>1\)
Ta có:
\(\dfrac{3}{10}< \dfrac{3}{9}\)
\(\dfrac{3}{11}< \dfrac{3}{9}\)
\(\dfrac{3}{12}< \dfrac{3}{9}\)
\(\dfrac{3}{13}< \dfrac{3}{9}\)
\(\dfrac{3}{14}< \dfrac{3}{9}\)
\(\Rightarrow S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}< 5.\dfrac{3}{9}\)
\(\Rightarrow S< \dfrac{5}{3}< 2\)

\(-\dfrac{1}{12}\) < \(\dfrac{x}{24}\) < \(\dfrac{1}{8}\)
- \(\dfrac{2}{24}\) < \(\dfrac{x}{24}\) < \(\dfrac{3}{24}\)
- 2 < \(x\) < 3
\(x\) \(\in\) {-1; 0; 1; 2}
Vậy \(x\) \(\in\) {-1; 0; 1; 2}

35%\(x\) + 0,5\(x\) + \(x\): 2 = 27
\(x\) \(\times\) 0,35 + \(x\) \(\times\) 0,5 + \(x\) \(\times\) 0,5 = 27
\(x\) \(\times\) (0,35 + 0,5 + 0,5) = 27
\(x\) \(\times\) 1,35 = 27
\(x\) = 27 : 1,35
\(x\) = 20
Vậy \(x\) = 20

\(M=\left(\dfrac{1}{2^2}-1\right)\left(\dfrac{1}{3^2}-1\right)\cdot...\cdot\left(\dfrac{1}{100^2}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{100}-1\right)\cdot\left(\dfrac{1}{2}+1\right)\cdot\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{100}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-99}{100}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{101}{100}\)
\(=\dfrac{1}{100}\cdot\dfrac{101}{2}=\dfrac{101}{200}\)

ta có n^2 +5 =n(n+1)-(n+1)+6chia hết cho n+1
mà n(n+1)chia hết cho n+1; n+1chia hết cho n+1
=> 6 chia hết cho n+1
=> n+1 thuộc ước của 6={1;-1;6;-6}
=>n thuộc {0;-2;5;-7}
Vậy n thuộc {0;-2;5;-7}
ta có n^2 +5 =n(n+1)-(n+1)+6chia hết cho n+1
mà n(n+1)chia hết cho n+1; n+1chia hết cho n+1
=> 6 chia hết cho n+1
=> n+1 thuộc ước của 6={1;-1;6;-6}
=>n thuộc {0;-2;5;-7}
Vậy n thuộc {0;-2;5;-7}

Câu 1:
Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB+4=10
=>AB=6(cm)
Vì BM<BA
nên M nằm giữa B và A
=>BM+MA=BA
=>MA+4=6
=>MA=2(cm)
Câu 2:
\(3xy+2x-5y=6\)
=>\(x\left(3y+2\right)-5y-\dfrac{10}{3}=\dfrac{8}{3}\)
=>\(3x\left(y+\dfrac{2}{3}\right)-5\left(y+\dfrac{2}{3}\right)=\dfrac{8}{3}\)
=>\(\left(3x-5\right)\left(3y+2\right)=8\)
=>\(\left(3x-5;3y+2\right)\in\left\{\left(1;8\right);\left(8;1\right);\left(-1;-8\right);\left(-8;-1\right);\left(2;4\right);\left(4;2\right);\left(-2;-4\right);\left(-4;-2\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(2;2\right);\left(\dfrac{13}{3};-\dfrac{1}{3}\right);\left(\dfrac{4}{3};-\dfrac{10}{3}\right);\left(-1;-1\right);\left(\dfrac{7}{3};\dfrac{2}{3}\right);\left(9;0\right);\left(1;-2\right);\left(\dfrac{1}{3};-\dfrac{4}{3}\right)\right\}\)
mà x,y nguyên
nên \(\left(x;y\right)\in\left\{\left(2;2\right);\left(-1;-1\right);\left(9;0\right);\left(1;-2\right)\right\}\)

\(8n-1⋮4n-5\)
\(\Rightarrow2\times4n-10+9⋮4n-5\)
\(\Rightarrow2\times4n-2\times5+9⋮4n-5\)
\(\Rightarrow2\left(4n-5\right)+9⋮4n-5\)
Vì \(2\left(4n-5\right)⋮4n-5\)
\(\Rightarrow9⋮4n-5\)
\(\Rightarrow4n-5\) \(\inƯ\left(9\right)=\left\{1,3,9,-1,-3,-9\right\}\)
\(\Rightarrow4n\in\left\{6;8;14;4;2;-4\right\}\)
mà \(4n⋮4\)
\(\Rightarrow4n\in\left\{8;4;-4\right\}\)
\(\Rightarrow n\in\left\{2,1,-1\right\}\)
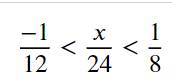
\(3\cdot\left(3x-\dfrac{1}{2}\right)^3+\dfrac{1}{9}=0\)
\(\Rightarrow3\cdot\left(3x-\dfrac{1}{2}\right)^3=-\dfrac{1}{9}\)
\(\Rightarrow\left(3x-\dfrac{1}{2}\right)^3=-\dfrac{1}{9}:3\)
\(\Rightarrow \left(3x-\dfrac{1}{2}\right)^3=-\dfrac{1}{27}\)
\(\Rightarrow\left(3x-\dfrac{1}{2}\right)^3=\left(-\dfrac{1}{3}\right)^3\)
\(\Rightarrow3x-\dfrac{1}{2}=-\dfrac{1}{3}\)
\(\Rightarrow3x=-\dfrac{1}{3}+\dfrac{1}{2}\)
\(\Rightarrow3x=\dfrac{1}{6}\)
\(\Rightarrow x=\dfrac{1}{6}:3=\dfrac{1}{18}\)