Với \(x,y,z\ne0\), ta có: \(x-y-z=0\Leftrightarrow\left\{{}\begin{matrix}x-z=y\\y-x=-z\\z+y=x\end{matrix}\right.\)\((*)\)

Mặt khác: \(B=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\)

\(=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}\)

Thay \((*)\) vào \(B\), ta được:

\(B=\dfrac{y}{x}\cdot\dfrac{-z}{y}\cdot\dfrac{x}{z}=-1\)

Vậy \(B=-1\) thoả mãn đề bài.

+ \(x-y-z=0\)
\(\Rightarrow\dfrac{x}{x}-\dfrac{\left(y+z\right)}{x}=0\) (Do \(x\ne0\))
\(\Leftrightarrow1-\dfrac{y+z}{x}=0\)
+ \(x-y-z=0\)
\(\Rightarrow\dfrac{\left(x-z\right)}{y}-\dfrac{y}{y}=0\) (Do \(y\ne0\))
\(\Leftrightarrow1-\dfrac{x-z}{y}=0\)
+ \(x-y-z=0\)
\(\Rightarrow\dfrac{\left(x-y\right)}{z}-\dfrac{z}{z}=0\) (Do \(z\ne0\))
\(\Leftrightarrow1-\dfrac{x-y}{z}=0\)
Ta có: \(B=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\)
\(=\left(1-\dfrac{x}{y}-\dfrac{z}{x}+\dfrac{zx}{xy}\right)\left(1+\dfrac{y}{z}\right)\)
\(=\left(1-\dfrac{x}{y}-\dfrac{z}{x}+\dfrac{z}{y}\right)\left(1+\dfrac{y}{z}\right)\)
\(=1+\dfrac{y}{z}-\dfrac{x}{y}-\dfrac{xy}{yz}-\dfrac{z}{x}-\dfrac{zy}{xz}+\dfrac{z}{y}+\dfrac{zy}{yz}\)
\(=1-\dfrac{y+z}{x}+1-\dfrac{x-z}{y}+1-\dfrac{x-y}{z}-1\)
\(=-1\)
Vậy \(B=-1\)

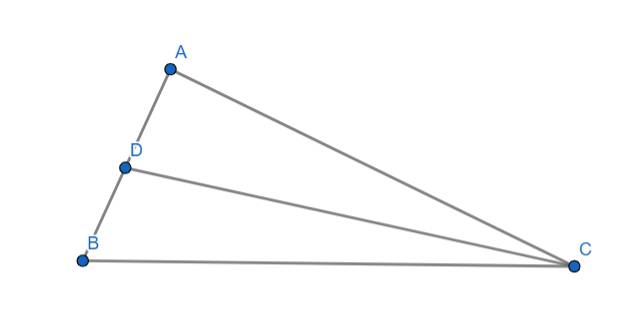
Gọi D là điểm người ta đặt loa phát thanh 

Trong `ΔACD` vuông tại A có CD là cạnh huyền `⇒ CD` là cạnh lớn nhất 

`⇒ CD > AC` 

Mà: `AC = 550(m) `

`⇒CD > 550` 

Vậy ở vị trí C không thể nghe rõ được tiếng của loa phát thanh 

Gọi D là điểm người ta đặt loa phát thanh 

Trong $\Delta ACD$ vuông tại A có CD là cạnh huyền $\Rightarrow CD$ là cạnh lớn nhất 

$\Rightarrow CD>AC$ 

Mà: $AC=550(m)$

$\Rightarrow CD>550$ 

Vậy ở vị trí C không thể nghe rõ được tiếng của loa phát thanh 

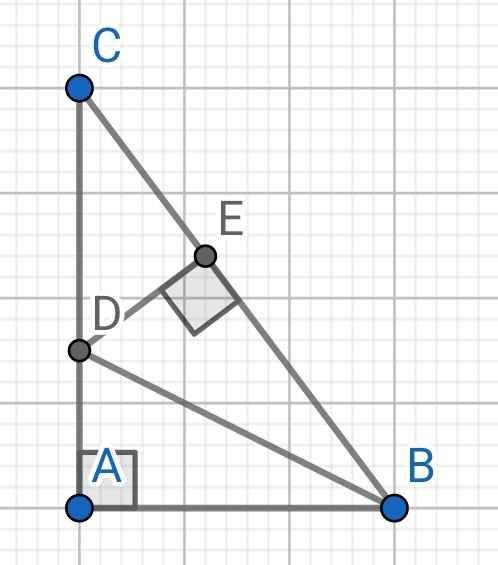
Do BD là tia phân giác của ∠ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠EBD

Xét hai tam giác vuông: ∆ABD và ∆EBD có:

BD là cạnh chung

∠ABD = ∠EBD (cmt)

⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)

b) Xem lại đề. Điểm F ở đâu ra?

a)Xét ΔABD và ΔEBD có:

góc A=góc E=90 độ

BD là cạnh chung

góc ABD=góc EBD

=>$\Delta ABD=\Delta EBD.$

1 người làm cỏ trên một cánh đồng hết số thời gian là:
 10 x 9 = 90 (giờ)
15 người làm cỏ trên một cánh đồng hết số thời gian là:
90 : 15 = 6 (giờ)
Đ/S:... (Cho con GP ạ)

Do năng suất của mỗi người là như nhau và cùng làm cỏ một cánh đồng nên số người và thời gian là hai đại lượng tỉ lệ nghịch

Thời gian 15 người làm cỏ cánh đồng đó:

10 . 9 : 15 = 6 (giờ)

Gọi x, y, z(kg) lần lượt là số giấy vụ ba chi đội 7A, 7B và 7C thu được (x, y, z > 0)
Theo đề bài, ta có:
\(\dfrac{x}{7}=\dfrac{y}{8}=\dfrac{z}{9}\) và \(x+y+z=120\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{7}=\dfrac{y}{8}=\dfrac{z}{9}=\dfrac{x+y+z}{7+8+9}=\dfrac{120}{24}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\cdot7=35\\y=5\cdot8=40\\z=5\cdot9=45\end{matrix}\right.\)
Vậy số kg giấy vụn ba chi đội 7A, 7B và 7C thu được lần lượt là 35kg, 40kg và 45kg

Để tính số giấy mỗi chi đội thu được, ta cần chia tổng số giấy vụn (120 kg) theo tỉ lệ 7:8:9 thành 3 phần.

Tổng số phần là 7 + 8 + 9 = 24

Số giấy mỗi chi đội 7A thu được: 120 x (7/24) = 35 kg Số giấy mỗi chi đội 7B thu được: 120 x (8/24) = 40 kg Số giấy mỗi chi đội 7C thu được: 120 x (9/24) = 45 kg

Vậy số giấy mỗi chi đội thu được lần lượt là: 35 kg, 40 kg, 45 kg.

a/\(\dfrac{x}{5}=\dfrac{-3}{15}\)
\(\dfrac{x}{5}=\dfrac{-1}{5}\)
\(x=-1\)
b/Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{17}=\dfrac{y}{12}=\dfrac{x-y}{17-12}=\dfrac{10}{5}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\cdot17=34\\y=2\cdot12=24\end{matrix}\right.\)

a/$\genfrac{}{}{0ex}{}{x}{5}=\genfrac{}{}{0ex}{}{-3}{15}$
$\genfrac{}{}{0ex}{}{x}{5}=\genfrac{}{}{0ex}{}{-1}{5}$
$x=-1$
b/Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
$\genfrac{}{}{0ex}{}{x}{17}=\genfrac{}{}{0ex}{}{y}{12}=\genfrac{}{}{0ex}{}{x-y}{17-12}=\genfrac{}{}{0ex}{}{10}{5}=2$
$\Rightarrow \{\begin{array}{c}x=2\cdot 17=34\\ y=2\cdot 12=24\end{array}$

 

a/Thay x = -6 vào biểu thức, ta có:
\(3\times\left(-6\right)+5\)
\(=-18+5\)
\(=-13\)
b/Thay m = -2 và n = -1 vào biểu thức, ta có:
\(2\cdot\left(-2\right)^2-3\cdot\left(-1\right)+7\)
\(=8+3+7\)
\(=18\)

a.

Tại \(x=-6\Rightarrow3x+5=3.\left(-6\right)+5=-13\)

b.

Tại \(m=-2;n=-1\)

\(2m^2-3n+7=2.\left(-2\right)^2-3.\left(-1\right)+7=18\)

a/Hệ số tỉ lệ k là:
\(k=xy=\left(-10\right)\cdot\left(-2\right)=20\)
b/
+) Khi \(x=4\) thì \(y=\dfrac{20}{x}=\dfrac{20}{4}=5\)
+) Khi \(x=-2\) thì \(y=\dfrac{20}{x}=\dfrac{20}{-2}=-10\)

a/Hệ số tỉ lệ k là:
$k=xy=\left(-10\right)\cdot \left(-2\right)=20$
b/
+) Khi $x=4$ thì $y=\genfrac{}{}{0ex}{}{20}{x}=\genfrac{}{}{0ex}{}{20}{4}=5$
+) Khi $x=-2$ thì $y=\genfrac{}{}{0ex}{}{20}{x}=\genfrac{}{}{0ex}{}{20}{-2}=-10$

a/Gọi x, y, z(cây) lần lượt là số cây ba lớp 7A, 7B và 7C trồng được nhân dịp Tết trồng cây
(x, y, z \(\in N\)*)
Theo đề bài, ta có:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}\) và \(x+y+z=180\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{x+y+z}{3+5+7}=\dfrac{180}{15}=12\)
\(\Rightarrow\left\{{}\begin{matrix}x=12\cdot3=36\\y=12\cdot5=60\\z=12\cdot7=84\end{matrix}\right.\)
Vậy ...
b/Gọi a, b, c(cm) lần lượt là độ dài ba cạnh của tam giác đó (a, b, c > 0)
Theo đề bài, ta có:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}\) và \(a+b+c=121\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{121}{11}=11\)
\(\Rightarrow\left\{{}\begin{matrix}a=11\cdot2=22\\b=11\cdot4=44\\c=11\cdot5=55\end{matrix}\right.\)
Vậy ...
#TiendatzZz

Ta có:

• Do M, N lần lượt là trung điểm của DF, DE nên ta có DM = MF và DN = NE.
• Vì MP = ME và MQ = NF nên ta có MP = ME = NF = NQ.
• Khi đó, ta có tứ giác MPNQ là hình thoi.
• Vậy, ta có D là trung điểm của PQ (do D là trung điểm của MN và MN là đường chéo của hình thoi MPNQ).
• Vậy, ta có D là trung điểm của PQ. Đpcm.