\(\dfrac{1}{2.3}\)+\(\dfrac{1}{3.4}\)+\(\dfrac{1}{4.5}\)+.....+\(\dfrac{1}{99.100}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(A=\dfrac{3n-4}{n-3}=\dfrac{3n-9+5}{n-3}=\dfrac{3\left(n-3\right)+5}{n-3}=3+\dfrac{5}{n-3}\)
Do 3 là số nguyên nên để A nguyên thì \(\dfrac{5}{n-3}\) là số nguyên
\(\Rightarrow n-3=Ư\left(5\right)\)
\(\Rightarrow n-3=\left\{-5;-1;1;5\right\}\)
\(\Rightarrow n=\left\{-2;2;4;8\right\}\)
Mà n là số tự nhiên \(\Rightarrow n=\left\{2;4;8\right\}\)

Sau khi hạ giá thì giá tiền của 1 cái áo là:
\(400000\times\dfrac{3}{4}=300000\) (đồng)
Giá vốn của cái áo là:
\(300000:\left(100\%+20\%\right)=250000\) (đồng)
Nếu không hạ giá thì cửa hàng lãi:
\(\dfrac{400000}{250000}\cdot100\%-100\%=60\%\) (giá vốn)
Giá của mỗi chiếc áo bán ngày 1/5 là:
\(400000.\dfrac{3}{4}=300000\) (đồng)
Do cửa hàng khi đó lãi 20% so với giá vốn nên giá vốn mỗi chiếc áo là:
\(300000:\left(100\%+20\%\right)=250000\) (đồng)
Nếu ko hạ giá thì cửa hàng lãi số % là:
\(\left(\dfrac{\left(400000-250000\right).100}{250}\right)\%=60\%\)

$1,23+(-5,48)+8,77-4,32$
$=(1,23+8,77)+[(-5,48)-4,32]$
$=10+(-9,8)$
$=0,2$

ý bạn là : 7 x 0,25 + 9 x( -0,25 ) á
=> 1,75 + 9 x( -0,25)
=>10 , 75 x -0,25
=>-26875
7 x 0,25 + 9 x (-0,25)
= 7 x 0,25 + (-9) x 0,25
= ( -9 + 7 ) x 0,25
= (-2) x 0,25
= -0,5

a: TH1: B nằm giữa A và C
=>AB+BC=AC
=>BC+5=3
=>BC=-2(loại)
TH2: A nằm giữa B và C
=>BC=BA+AC=5+3=8(cm)
TH3: C nằm giữa A và B
=>CA+CB=AB
=>CB+3=5
=>CB=2(cm)
b: Số cách chọn 2 điểm trong 7 điểm nằm trên đường thẳng xy là: \(C^2_7=21\left(cách\right)\)
=>Có 21 tam giác tạo thành từ 3 điểm bất kì trong hình vẽ

Cảm ơn bạn nhưng yêu cầu bạn không đăng lung tung lên diễn đàn!

\(1+\dfrac{1}{3}+\dfrac{1}{6}+...+\dfrac{2}{x\left(x+1\right)}=1\dfrac{2025}{2027}\)
=>\(\dfrac{2}{2}+\dfrac{2}{6}+\dfrac{2}{12}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{4052}{2027}\)
=>\(2\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{4052}{2027}\)
=>\(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{2026}{2027}\)
=>\(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{2026}{2027}\)
=>\(1-\dfrac{1}{x+1}=\dfrac{2026}{2027}\)
=>\(\dfrac{1}{x+1}=\dfrac{1}{2027}\)
=>x+1=2027
=>x=2026
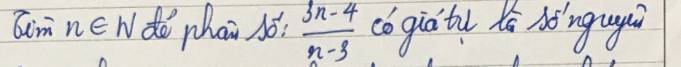

\(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{99.100}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=\dfrac{1}{2}-\dfrac{1}{100}\)
\(=\dfrac{50}{100}-\dfrac{1}{100}=\dfrac{49}{100}\)
=1- 1/2+1/2 - 1/3+1/3 - ... -1/99+1/99-1/100
=1-1/100
=99/100