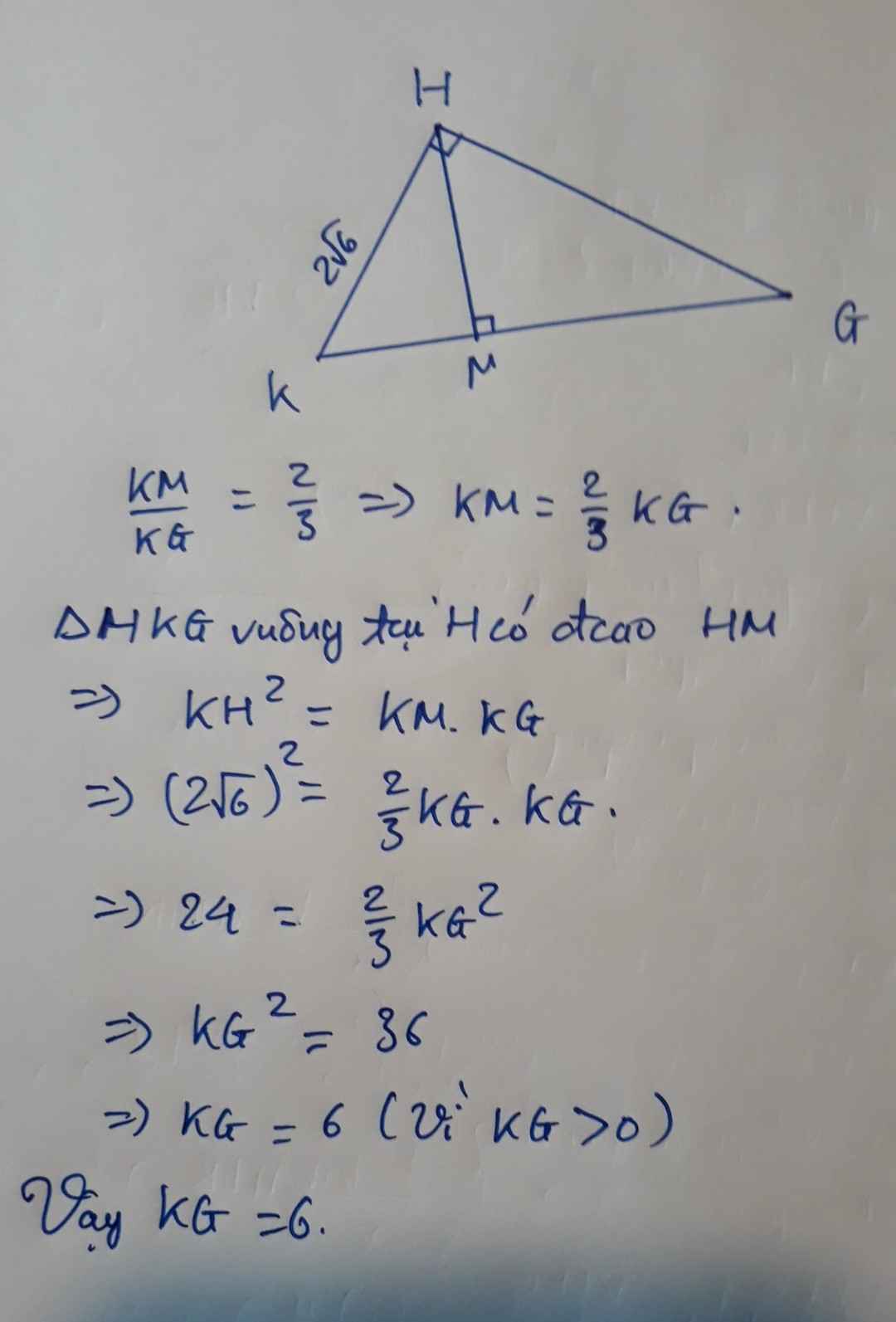
b5: cho tam giác HKG vuông tại H, HM vuông KG ( M thuộc KG ), KM/KG=2/3, HK= 2 căn 6. Tính KG
b6: tam giác ABC vuông tại A. đường cao AH, AB = 15cm, CH= 16cm. tính chu vi tam giác ABC
b7: cho tam giác ABC nhọn, hai đường cao BD,CE cắt nhau tại H, trên đoạn HB và HC lần lượt lấy điểm M,N sao cho góc AMC= góc ANB= 90độ. chứng minh tam giác AMN cân