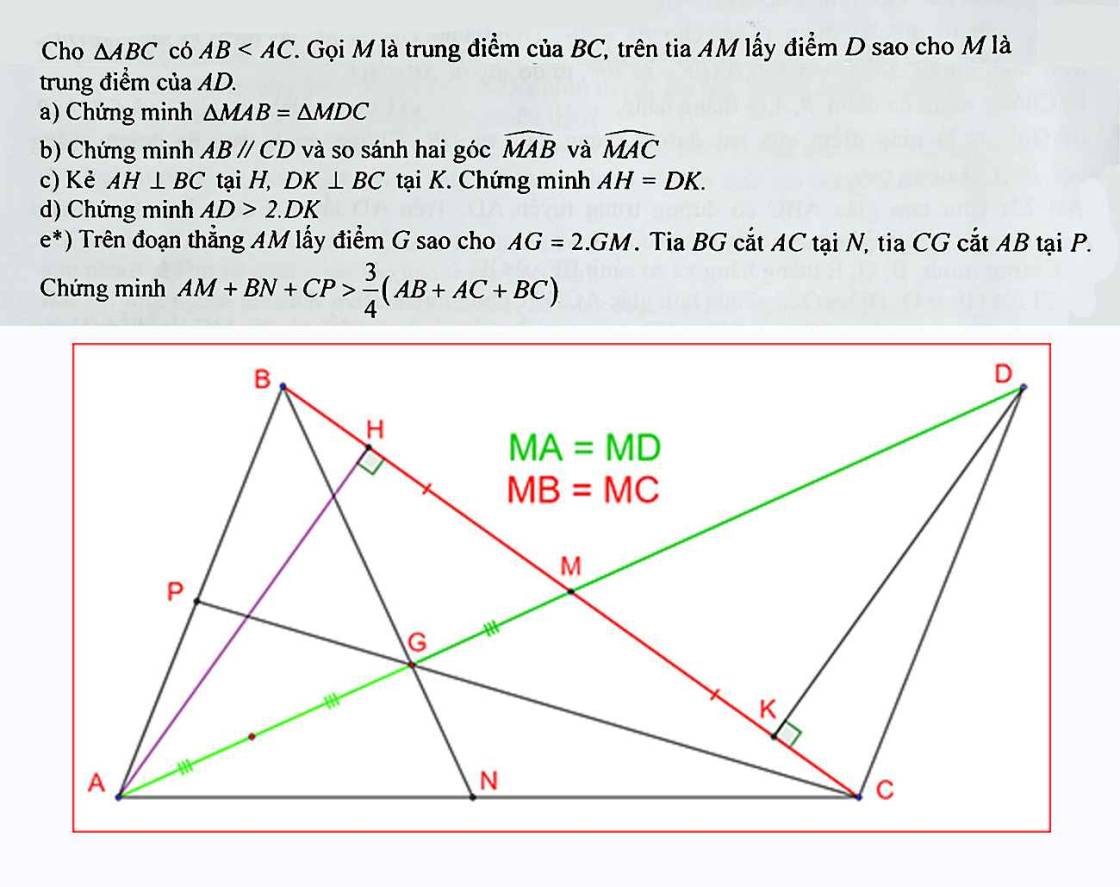
Cho tam giác ABC nhọn(AB < AC).Trên tia đối của tia AB lấy điểm E sao cho AE = AB, Trên tia đối tia AC lấy diểm F sao cho AF = AC.
a)Chứng minh BF = CE và EF // BC.
b)Trên các cạnh BF và CE lấy thứ tự các điểm M, N sao cho BM = 2MF và CE = 3CN. Chứng minh 3 điểm M, A, N thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: ta có: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
Ta có: ΔMAB=ΔMCD
=>AB=CD
mà AB<AC
nên CD<CA
=>\(\widehat{CAD}< \widehat{CDA}\)
mà \(\widehat{CDA}=\widehat{BAM}\)
nên \(\widehat{CAM}< \widehat{BAM}\)
c: Xét ΔAHM vuông tại H và ΔDKM vuông tại K có
MA=MD
\(\widehat{AMH}=\widehat{DMK}\)(hai góc đối đỉnh)
Do đó: ΔAHM=ΔDKM
=>AH=DK
d: Ta có: AM>AH(ΔAHM vuông tại H)
DM>DK(ΔDKM vuông tại K)
Do đó: AM+DM>AH+DK
=>AD>2DK
e:
Ta có: AG=2GM
mà AG+GM=AM
nên \(AG=\dfrac{2}{3}AM\)
Xét ΔBAC có
AM là đường trung tuyến
\(AG=\dfrac{2}{3}AM\)
Do đó: G là trọng tâm của ΔABC
Xét ΔABC có
G là trọng tâm của ΔABC
BG cắt AC tại N
CG cắt AB tại P
Do đó: N là trung điểm của AC, P là trung điểm của AB
Xét ΔABC có
G là trọng tâm của ΔABC
BN,CP là các đường trung tuyến
Do đó: \(BG=\dfrac{2}{3}BN;CG=\dfrac{2}{3}CP\)
Xét ΔGAB có GA+GB>AB
Xét ΔGAC có GA+GC>AC
Xét ΔGBC có GB+GC>BC
Do đó: \(2\left(GA+GB+GC\right)>AB+AC+BC\)
=>\(GA+GB+GC>\dfrac{AB+AC+BC}{2}\)
=>\(\dfrac{2}{3}\left(AM+BN+CP\right)>\dfrac{AB+AC+BC}{2}\)
=>\(AM+BN+CP>\dfrac{3}{4}\cdot\left(AB+AC+BC\right)\)

\(\dfrac{2}{3}:\left(x-\dfrac{1}{3}\right)^3-9=\dfrac{23}{3}\)
=>\(\dfrac{2}{3}:\left(x-\dfrac{1}{3}\right)^3=\dfrac{23}{3}+9=\dfrac{50}{3}\)
=>\(\left(x-\dfrac{1}{3}\right)^3=\dfrac{2}{3}:\dfrac{50}{3}=\dfrac{1}{25}\)
=>\(x-\dfrac{1}{3}=\dfrac{\sqrt[3]{5}}{5}\)
=>\(x=\dfrac{\sqrt[3]{5}}{5}+\dfrac{1}{3}=\dfrac{3\sqrt[3]{5}+5}{15}\)

x/2=y/3 => x/8=y/12
y/4=z/5 => y/12=z/15
=> x/8=y/12=z/15=x+y+z/8+12+15=5/35=1/7
x/8=1/7 y/12=1/7 z/15=1/7
x=8*1/7=8/7 y=12*1/7=12/7 z=15*1/7=15/7

A) vì ΔABC là Δ vuông tại A nên \(\widehat{A}=90^0\)
số đo của \(\widehat{C}\) là: \(\widehat{B}+\widehat{C}=\widehat{A}\Rightarrow\widehat{C}=\widehat{A}-\widehat{B}=90^0-60^0=30^0\)
TA CÓ: \(\widehat{A}>\widehat{B}>\widehat{C}\)
\(\Rightarrow BC>AC>AB\)
b) xét Δ vuông ABE và Δ vuông HBE, có:
\(\widehat{ABE}=\widehat{HBE}\left(gt\right)\)
BE là cạnh chung
⇒ ΔABE = ΔHBE (ch-gn)
⇒ AB = BH (2 cạnh tương ứng)
xét ΔABH có: AB = BH (cmt)
⇒ ΔABH là Δ cân

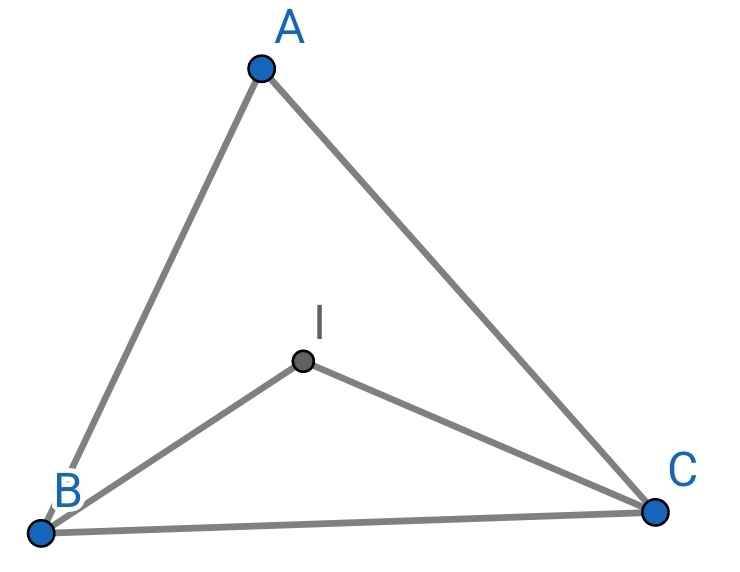
a) Ta có:
∠BAC + ∠ABC + ∠ACB = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠ABC + ∠ACB = 180⁰ - ∠BAC
= 180⁰ - 80⁰
= 100⁰
Do BI là tia phân giác của ∠ABC (gt)
⇒ ∠IBC = ∠ABC : 2
Do CI là tia phân giác của ∠ACB (gt)
⇒ ∠ICB = ∠ACB : 2
⇒ ∠IBC + ∠ICB = ∠ABC : 2 + ∠ACB : 2
= (∠ABC + ∠ACB) : 2
= 100⁰ : 2
= 50⁰
Ta có:
∠IBC + ∠ICB + ∠BIC = 180⁰ (tổng ba góc trong ∆IBC)
⇒ ∠BIC = 180⁰ - (∠IBC + ∠ICB)
= 180⁰ - 50⁰
= 130⁰
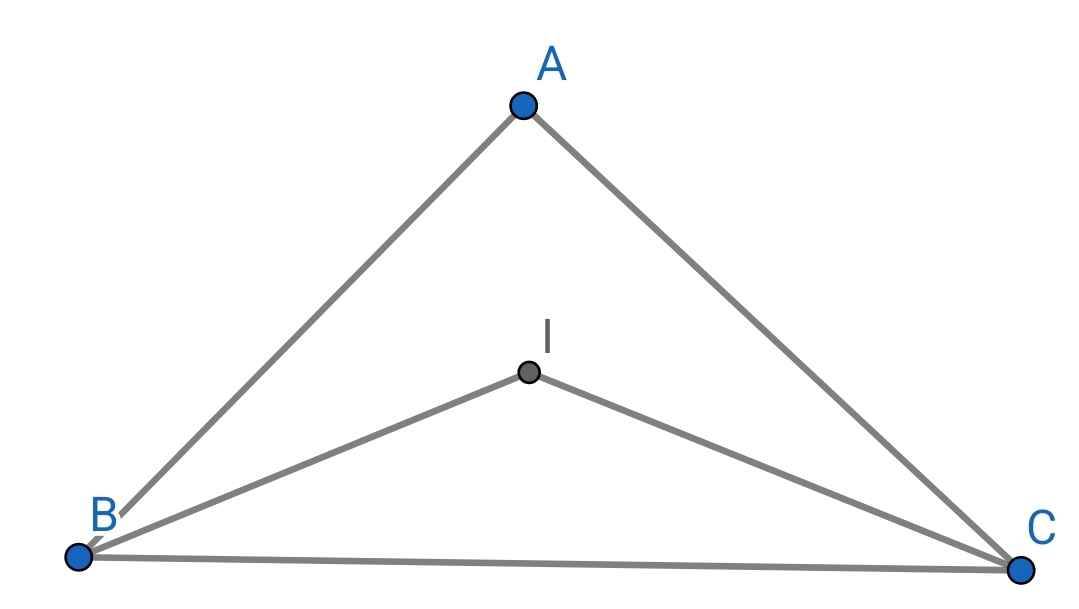
b) Ta có:
∠BAC + ∠ABC + ∠ACB = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠ABC + ∠ACB = 180⁰ - ∠BAC
= 180⁰ - 120⁰
= 60⁰
Do BI là tia phân giác của ∠ABC (gt)
⇒ ∠IBC = ∠ABC : 2
Do CI là tia phân giác của ∠ACB (gt)
⇒ ∠ICB = ∠ACB : 2
⇒ ∠IBC + ∠ICB = ∠ABC : 2 + ∠ACB : 2
= (∠ABC + ∠ACB) : 2
= 60⁰ : 2
= 30⁰
Ta có:
∠IBC + ∠ICB + ∠BIC = 180⁰ (tổng ba góc trong ∆IBC)
⇒ ∠BIC = 180⁰ - (∠IBC + ∠ICB)
= 180⁰ - 30⁰
= 150⁰
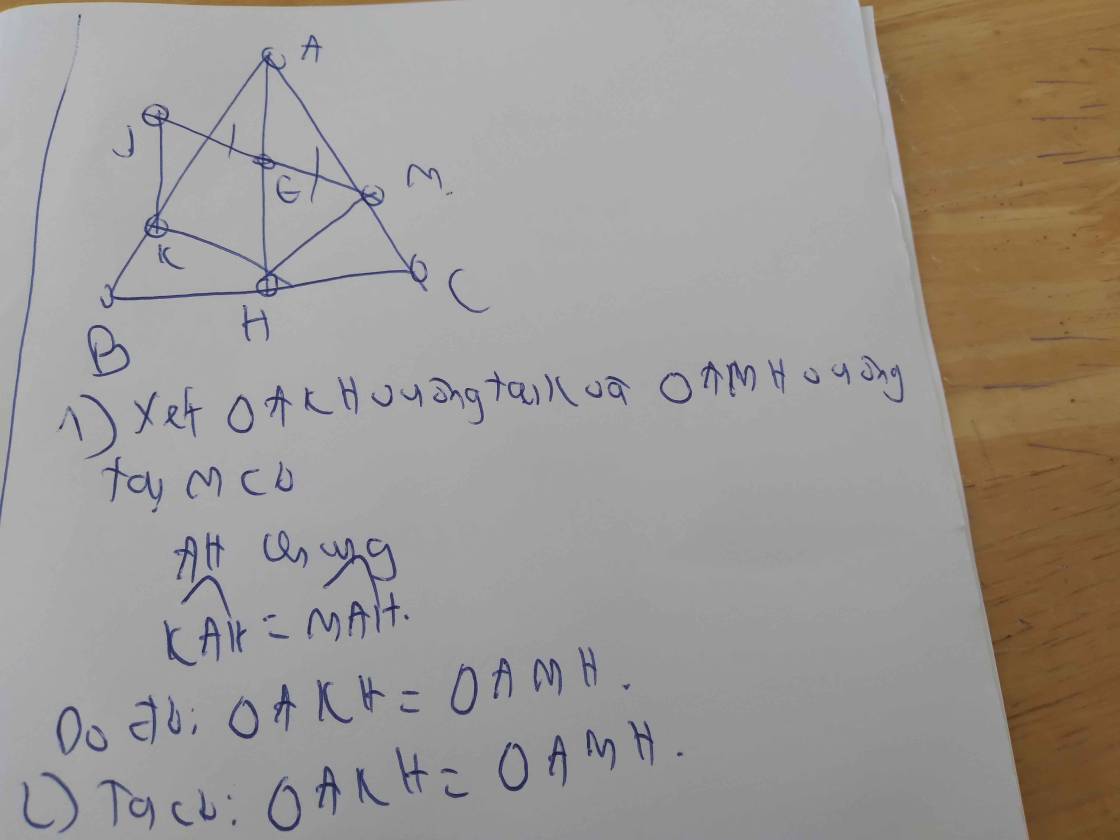


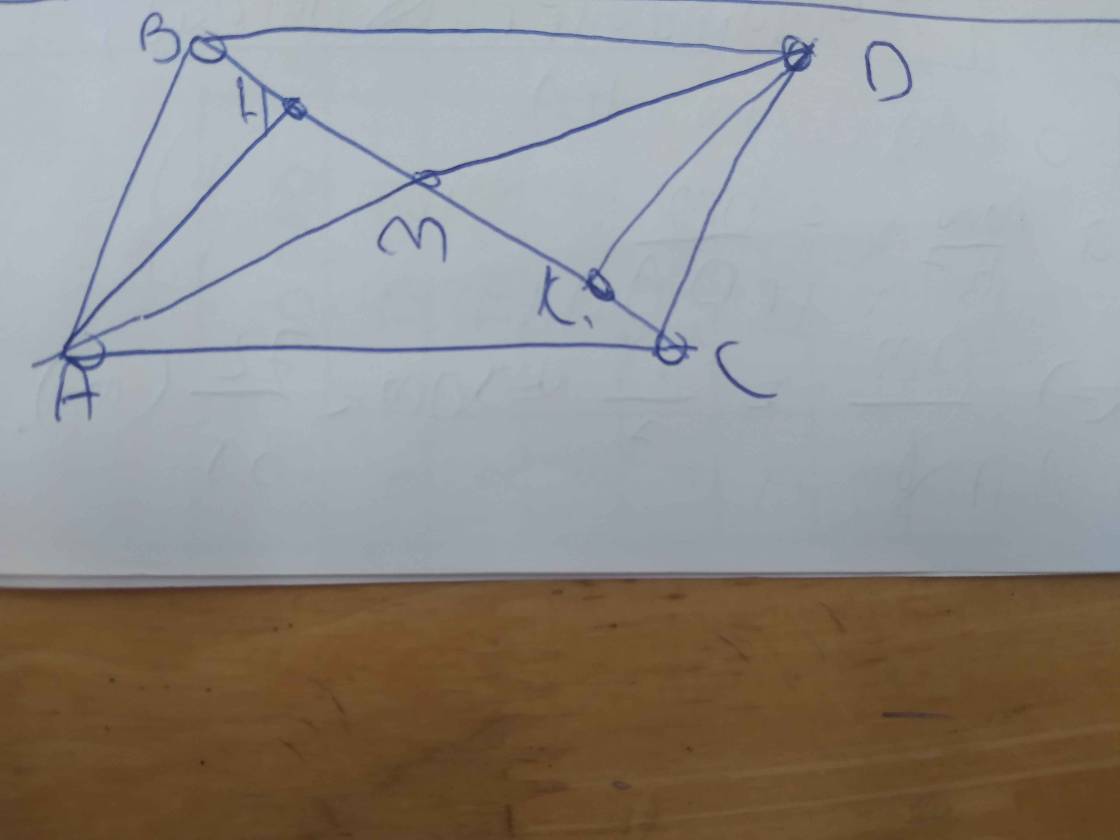


a: Xét ΔABF và ΔAEC có
AB=AE
\(\widehat{BAF}=\widehat{EAC}\)(hai góc đối đỉnh)
AF=AC
Do đó: ΔABF=ΔAEC
=>BF=EC
Xét ΔAEF và ΔABC có
AE=AB
\(\widehat{EAF}=\widehat{BAC}\)(hai góc đối đỉnh)
AF=AC
Do đó: ΔAEF=ΔABC
=>\(\widehat{AEF}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EF//BC
b: Ta có: FM+MB=FB
=>FB=2MF+MF=3MF
mà CE=3CN
và FB=CE
nên MF=CN
Xét ΔAFM và ΔACN có
AF=AC
\(\widehat{AFM}=\widehat{ACN}\)(ΔAFB=ΔACE)
FM=CN
Do đó: ΔAFM=ΔACN
=>\(\widehat{FAM}=\widehat{CAN}\)
mà \(\widehat{FAM}+\widehat{MAC}=180^0\)(hai góc kề bù)
nên \(\widehat{CAN}+\widehat{CAM}=180^0\)
=>M,A,N thẳng hàng