a, \(x^2\) + 4\(x\) - y² + 4

= (\(x^2\) + 4\(x\) + 4) - y²

= (\(x\) + 2)² - y²

= (\(x\) + 2 - y)(\(x\) + 2 + y)

b, 2\(x^2\) - 18

= 2.(\(x^2\) -9)

= 2.(\(x\) -3).(\(x\) + 3)

Các đơn thức là :

\(\left(1-\dfrac{1}{\sqrt[]{3}}\right)x^2;x^2.\dfrac{7}{2}\)

b, (\(x^2\) - \(xy\) ) + (\(x-y\))

= (\(x-y\)).\(x\) + (\(x-y\))

= (\(x-y\)).(\(x\) + 1)

c, \(x^2\) - 2\(x\) - 15

= (\(x^2\) - 2\(x\) + 1) - 16

= (\(x\) - 1)² - 4²

= (\(x-1-4\)).(\(x-1+4\))

= (\(x-5\)).(\(x+3\))

Các đơn thức là :

\(\dfrac{x^2y}{2};\dfrac{x}{-5^2};\dfrac{-4}{5}\)

a) \(4x^2-16+\left(3x+12\right)\left(4-2x\right)\)

\(=\left(2x-4\right)\left(2x+4\right)-3\left(x+4\right)\left(2x-4\right)\)

\(=\left(2x-4\right)\left(2x+4-3x-12\right)\)

\(=-\left(2x-4\right)\left(x+8\right)\)

b) \(x^3+x^2y-15x-15y\)

\(=x^2\left(x+y\right)-15\left(x+y\right)\)

\(=\left(x+y\right)\left(x^2-15\right)\)

c) \(3\left(x+8\right)-x^2-8x\)

\(=3\left(x+8\right)-x\left(x+8\right)\)

\(=\left(x+8\right)\left(3-x\right)\)

d) \(x^3-3x^2+1-3x\)

\(=x^3+1-3x^2-3x\)

\(=\left(x+1\right)\left(x^2-x+1\right)-3x\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2-x+1-3x\right)\)

\(=\left(x+1\right)\left(x^2-4x+1\right)\)

d) \(5x^2-5y^2-20x+20y\)

\(=5\left(x^2-y^2\right)-20\left(x-y\right)\)

\(=5\left(x-y\right)\left(x+y\right)-20\left(x-y\right)\)

\(=5\left(x-y\right)\left(x+y-4\right)\)

b) \(x^2y-x^3-10y+10x\)

\(=x^2\left(y-x\right)-10\left(y-x\right)\)

\(=\left(y-x\right)\left(x^2-10\right)\)

c) \(x^2\left(x-2\right)+49\left(2-x\right)\)

\(=\left(x-2\right)\left(x^2-49\right)\)

\(=\left(x-2\right)\left(x-7\right)\left(x+7\right)\)

a) \(x^2-y^2-3x+3y\)

\(=\left(x-y\right)\left(x+y\right)-3\left(x-y\right)\)

\(=\left(x-y\right)\left(x+y-3\right)\)

b) \(2x+2y-x^2+y^2\)

\(=2\left(x+y\right)-\left(x^2-y^2\right)\)

\(=2\left(x+y\right)-\left(x-y\right)\left(x+y\right)\)

\(=\left(x+y\right)\left(2-x+y\right)\)

c) \(x^2-16+y^2+2xy\)

\(=x^2+y^2+2xy-16\)

\(=\left(x+y\right)^2-16\)

\(=\left(x+y+4\right)\left(x+y-4\right)\)

a) \(x^2-y^2-3x+3y\)

\(=\left(ax+y\right)\left(ax-y\right)-3.\left(x-y\right)\)

b) \(2x+2y-x^2+y^2\)

\(=2\left(x+y\right)-\left(x+y\right)\left(x-y\right)\)

c) \(x^2-16+y^2+2xy\)

\(=\left(x+y\right)\left(x-y\right)+2xy-16\)

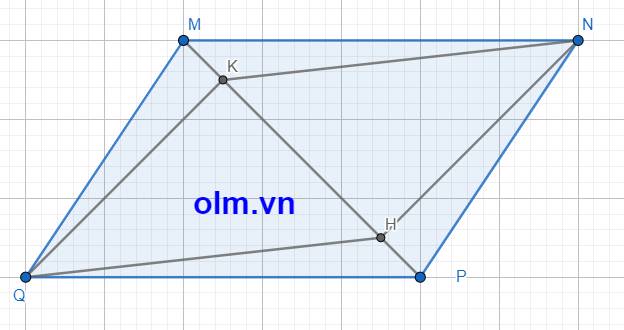
Xét \(\Delta\) MQP và \(\Delta\) PNM có:

MP chung;  MQ = NP; QP = MN  (vì MNPQ là hình bình hành)

⇒ \(\Delta\)MQP = \(\Delta\) PNM ( c-c-c)

⇒ S_MQP = S_PNM 

   ⇒ QK = HN⁽¹⁾ ( vì hai tam giác có diện tích bằng nhau và chung cạnh đáy thì hai chiều cao tương ứng của hai tam giác đó bằng nhau)

Mặt khác QK \(\perp\) MP

               NH \(\perp\) MP

              ⇒ QH // NH⁽²⁾ ( vì hai đường thẳng cùng vuông với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau)

Kết hợp (1) và (2) ta có 

Tứ giác NHQK là hình bình hành ( vì tứ giác có một cặp cạnh đối diện song song và bằng nhau thì tứ giác đó là hình bình hành) 

\(\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)\)

\(=x^3+1-\left(x^3-1\right)\)

\(=x^3+1-x^3+1\)

\(=2\)